| 内容要旨 | | 古典的な数論において、Kummer-Sinnott[6]により示された指数-類数公式が良く知られている。この公式は円分体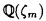 (ここに (ここに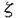 m=exp(2 m=exp(2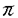 i/m))で円単数の指数と極大実部分体 i/m))で円単数の指数と極大実部分体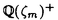 の類数がほとんど一致することを示している。GalovichとRosen[1]は有限体上の一変数有理関数体におけるこの結果の類似を示した。本論文では有限体上の大域関数体で[6]や[1]の理論を一般化した。この場合基礎体の類群の非自明性や無限因子の次数は任意であることに由来する困難が生じる。また、この指数公式の一つの応用も与える。以下ではこの結果を詳しく述べることにする。 の類数がほとんど一致することを示している。GalovichとRosen[1]は有限体上の一変数有理関数体におけるこの結果の類似を示した。本論文では有限体上の大域関数体で[6]や[1]の理論を一般化した。この場合基礎体の類群の非自明性や無限因子の次数は任意であることに由来する困難が生じる。また、この指数公式の一つの応用も与える。以下ではこの結果を詳しく述べることにする。 まず、kを有限体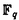 上の滑らかな射影曲線の関数体とする。∞をこの曲線の次数d∞の閉点とする。 上の滑らかな射影曲線の関数体とする。∞をこの曲線の次数d∞の閉点とする。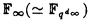 を∞での 剰余体、k∞を∞でのkの完備化とする。そして、Aを∞以外で正則な関数からなっているkの部分環とする。環Rに対し、R*はその単数群を表す。ここで、符号関数sgn: を∞での 剰余体、k∞を∞でのkの完備化とする。そして、Aを∞以外で正則な関数からなっているkの部分環とする。環Rに対し、R*はその単数群を表す。ここで、符号関数sgn: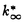 → →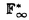 [定義4.1,3]を一つ固定する。Keは(k,∞,sgn)の正規体、また、Aの非自明なイデアルmに対し、K=Kmは(k,∞,sgn)の導手mに関する円分拡大である。これらはDrinfeld加群を使って定義された。He(また、H=Hm)はKe(また、Km)の極大実部分体、すなわち、∞が完全分解するKe(また、Km)の極大部分体である。Hayesの結果より[§15-16,4]、Heは(k,∞)のHilbert類体、また、Hは(k,∞)の導手mにおける環類体である。また、G1=Gal(He/k)である。N=Nmはp|mを満たす素イデアルに対するArtin記号 [定義4.1,3]を一つ固定する。Keは(k,∞,sgn)の正規体、また、Aの非自明なイデアルmに対し、K=Kmは(k,∞,sgn)の導手mに関する円分拡大である。これらはDrinfeld加群を使って定義された。He(また、H=Hm)はKe(また、Km)の極大実部分体、すなわち、∞が完全分解するKe(また、Km)の極大部分体である。Hayesの結果より[§15-16,4]、Heは(k,∞)のHilbert類体、また、Hは(k,∞)の導手mにおける環類体である。また、G1=Gal(He/k)である。N=Nmはp|mを満たす素イデアルに対するArtin記号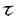 p=(p,He/k)で生成されるG1の部分群である。そして、e=[G1:N]を指数とする。最後にC=CmをKの円単数群とする(定義1.3)。最初の結果はCの階数の計算である。 p=(p,He/k)で生成されるG1の部分群である。そして、e=[G1:N]を指数とする。最後にC=CmをKの円単数群とする(定義1.3)。最初の結果はCの階数の計算である。 定理A.rankC=[H:k]-e この定理はD.Gossの一つの予想[2.7Conjecture,2]の証明を与えている。また、この定理はmがNm=G1を満さない場合、Cの階数はKの全単数群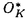 の階数より真に小さいことを示している。本論文ではKeの最大な階数を持つ不分岐楕円単数群 の階数より真に小さいことを示している。本論文ではKeの最大な階数を持つ不分岐楕円単数群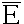 (定義2.2)を構成し、自然にCを拡張し、Kの最大な階数を持つ拡大された円単数群 (定義2.2)を構成し、自然にCを拡張し、Kの最大な階数を持つ拡大された円単数群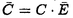 を構成した。Nm=G1の場合、C= を構成した。Nm=G1の場合、C=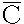 となる。定理Bでは となる。定理Bでは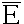 や や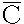 の全単数群内の指数を与える。任意の有限次拡大E/kにおいて、OEをE内での の全単数群内の指数を与える。任意の有限次拡大E/kにおいて、OEをE内での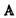 の整閉包、 の整閉包、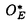 をEの単数群、h(OE)をEのイデアル類数、h(E)をEの因子類数とおく。また、 をEの単数群、h(OE)をEのイデアル類数、h(E)をEの因子類数とおく。また、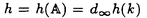 とおく。sはmの相異なる素因子の個数である。 とおく。sはmの相異なる素因子の個数である。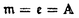 の時、s=0、また、 の時、s=0、また、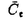 = =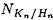 と約束する。 と約束する。 定理B.s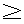 3の場合、(h,q-1)=1と仮定すると 3の場合、(h,q-1)=1と仮定すると 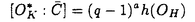 ここでs=0また1ならa=0、s>1ならa=e(2s-2-1)-(s-2)。 驚くべきことに、この指数公式はhやd∞と関係しない。Galovich-Rosenの定理は、この定理の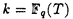 と∞=1/Tの場合である。本論文では[ と∞=1/Tの場合である。本論文では[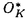 : :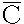 ]の計算で出て来る一つの指数をGalovichとRosen、Sinnottらの方法より簡単な、新しい方法を使って定理Bを証明する。 ]の計算で出て来る一つの指数をGalovichとRosen、Sinnottらの方法より簡単な、新しい方法を使って定理Bを証明する。 次の定理はこの定理Bの一つの応用である。古典的な数論において、Kummer判定法は円分体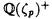 (ここにpは素数である)の類数のp-可除性の判定の重要的な定理である。Okadaは有限体上の一変数有理関数体におけるこの判定の類似を示した。有限体上の大域関数体(k,∞)において、pはkの標数、また、 (ここにpは素数である)の類数のp-可除性の判定の重要的な定理である。Okadaは有限体上の一変数有理関数体におけるこの判定の類似を示した。有限体上の大域関数体(k,∞)において、pはkの標数、また、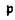 は は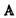 の素イデアルとする。d∞=1の時、L.Shu[5]は の素イデアルとする。d∞=1の時、L.Shu[5]は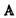 のBernoulliイデアルを定義して、h( のBernoulliイデアルを定義して、h(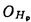 )/h( )/h(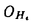 )のp-可除性の判定を与えた。本論文は一般的なd∞に対し、 )のp-可除性の判定を与えた。本論文は一般的なd∞に対し、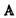 のBernoulliイデアルを定義して、h( のBernoulliイデアルを定義して、h(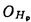 )のp-可除性の判定法を与える。Biは第i Bernoulliイデアル(定義8.3)とする。 )のp-可除性の判定法を与える。Biは第i Bernoulliイデアル(定義8.3)とする。 定理C.d=degp>1とする。この時、もしp|h(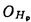 )ならば、1<i<qd-1かつi≡0(mod(q-1))を満たすある正整数iに対し、p|Biが成り立つ。 )ならば、1<i<qd-1かつi≡0(mod(q-1))を満たすある正整数iに対し、p|Biが成り立つ。 本論文では、定理Cに現れるこれのBernoulliイデアルについても零にならないことを証明する(命題10.2)。 参考論文1.S.Galovich and M.Rosen,Units and class group in cyclotomic function fields,J.Number Theory 14(1982),156-184.2.D.Goss,The 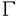 -ideal and special zeta-values,Duke Math.J.47(1980),345-364.3.D.Hayes,Stickelberger elements in function fields,Compositio Math.55(1985),209-235.4.D.Hayes,A brief introduction to Drinfeld modules,in "The Arithmetic of Function Fields"(D.Goss,D.Hayes,M.Rosen,Ed.)(1992),W.de Gruyter,Berlin,1-32.5.L.Shu,Kummer’s criterion over global function fields,J.Number Theory 49(1994),319-359.6.W.Sinnott,On the Stickelberger ideal and the circular units of a cyclotomic field,Ann.of Math.108(1978),107-134. -ideal and special zeta-values,Duke Math.J.47(1980),345-364.3.D.Hayes,Stickelberger elements in function fields,Compositio Math.55(1985),209-235.4.D.Hayes,A brief introduction to Drinfeld modules,in "The Arithmetic of Function Fields"(D.Goss,D.Hayes,M.Rosen,Ed.)(1992),W.de Gruyter,Berlin,1-32.5.L.Shu,Kummer’s criterion over global function fields,J.Number Theory 49(1994),319-359.6.W.Sinnott,On the Stickelberger ideal and the circular units of a cyclotomic field,Ann.of Math.108(1978),107-134. |
| 審査要旨 | | 円単数群について,それの全単数群の中での指数と,円分体の類数との関係の研究は,Kummerの有名な研究にはじまるもので,それは岩沢理論の出発点でもある.Kummerは,素数(巾)位数の1の巾根を添加して得られる円分体の円単数について,その指数と類数の関係を明らかにした.意外なことに,この結果の,一般位数の1のべき根を添加して得られる円分体への拡張は遅れ,1978年になってようやく,Sinnottによってなされた. 印林生氏が学位論文において研究したのは,この古典的な結果の,関数体上の類似である.代数体と関数体の類似は,整数論の基本原理であるが,関数体上の円分拡大の類似は,Drinfeld加群を使って定義される.印氏は,こうして定義される円単数について,その指数と類数との関係を明らかにした.この結果は,関数体が有理関数体である場合の,Galovich-Rosenの結果や,素数巾位数の場合のShuの結果を一般の場合に拡張するものである. 結果を述べるため,記号をいくつか導入する.kを有限体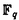 上の代数曲線Cの関数体とし,ある閉点∞の外で正則な関数全体のなす環をAとする.A上の環R上のDrinfeld加群 上の代数曲線Cの関数体とし,ある閉点∞の外で正則な関数全体のなす環をAとする.A上の環R上のDrinfeld加群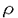 とは,環の準同型A→EndR( とは,環の準同型A→EndR(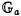 )で,接空間への作用が与えられた準同型A→Rと一致するもののことをいう.ここで )で,接空間への作用が与えられた準同型A→Rと一致するもののことをいう.ここで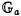 は,R上の代数群としての加法群を表す.K∞を∞での局所体,F∞を∞での剰余体とし,群の準同型sgn: は,R上の代数群としての加法群を表す.K∞を∞での局所体,F∞を∞での剰余体とし,群の準同型sgn: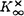 → →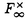 である条件を満たすものを1つとる.Hayesはこの準同型sgnにたいし,sgn-正規化されたDrinfeld加群と呼ばれるものを定義した.Aのイデアルmにたいし,Kmでkの導手m×∞の射線類体を表すことにするとsgn-正規化されたDrinfeld加群はすべてK(1)上定義され,しかもそれらの同型類の集合はGal(K(1)/k)-主等質空間になる.類体論よりGal(K(1)/k)はAのイデアル類群Cl(A)の である条件を満たすものを1つとる.Hayesはこの準同型sgnにたいし,sgn-正規化されたDrinfeld加群と呼ばれるものを定義した.Aのイデアルmにたいし,Kmでkの導手m×∞の射線類体を表すことにするとsgn-正規化されたDrinfeld加群はすべてK(1)上定義され,しかもそれらの同型類の集合はGal(K(1)/k)-主等質空間になる.類体論よりGal(K(1)/k)はAのイデアル類群Cl(A)の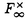 / /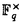 による拡大である. による拡大である. このとき円分拡大K=Km=k(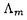 )の円単数群Cmは次のように定義される. )の円単数群Cmは次のように定義される.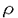 をsgn-正規化されたDrinfeld加群とし,P=Pmを をsgn-正規化されたDrinfeld加群とし,P=Pmを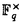 と と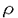 のm分点 のm分点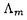 の座標によって生成される の座標によって生成される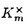 の部分群とする.C=CmをP∩ の部分群とする.C=CmをP∩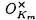 と定義する.Cの階数について, と定義する.Cの階数について, 命題1. が成り立つ.ここでHmはKm内の最大総実部分体(∞が完全分解するもののうちで最大)であり,emはイデアル類群Cl(A)の中でmの素因子によって生成される部分Nmの指数である. が論文中で示されている.これはGossか提出した問題に解答を与えるものである. 命題と単数定理より,Nm=Cl(A)でなければ,Cは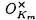 の指数有限部分群とはならない.そこで印氏はCを拡張し,n⊂mかつNm=Cl(A)を満たすnについてのCnのある部分群Enと元のCmを使って,拡張された円単数群 の指数有限部分群とはならない.そこで印氏はCを拡張し,n⊂mかつNm=Cl(A)を満たすnについてのCnのある部分群Enと元のCmを使って,拡張された円単数群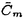 を定義した.多少不正確な言い方をすれば,EnはCnのノルム を定義した.多少不正確な言い方をすれば,EnはCnのノルム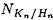 による像とほぼ等しい.このについて, による像とほぼ等しい.このについて, 定理1.mの素因子の個数sが,2以下でなければ,kの類数h=Card Cl(A)はq-1と互いに素であると仮定する.このとき が成り立つ.ここでa=0(s=0,1のとき),=em(23-2-1)-(s-2)(s>1のとき)であり,h(OH)は最大総実部分体H=Hmの類数Card Cl(OH)である. 応用としては,次のKummerの判定法の類似が与えられている.Kummerは上で述べた研究に引き続き,円分体の類数と,Bernoulli数の関係を研究し,素数pが円分体の実部分体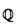 ( (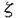 p)+の類数を割るための条件を,Bernoulli数の言葉で表した.ここでは,この結果の関数体での類似が与えられている.これは無限遠点∞の次数が1の場合のShuの結果を拡張するものであり,Aの素イデアルpについて,kの標数pがHPの類数を割るための条件を,AのBernoulliイデアルの言葉で与えている. p)+の類数を割るための条件を,Bernoulli数の言葉で表した.ここでは,この結果の関数体での類似が与えられている.これは無限遠点∞の次数が1の場合のShuの結果を拡張するものであり,Aの素イデアルpについて,kの標数pがHPの類数を割るための条件を,AのBernoulliイデアルの言葉で与えている. 最後に定理の証明の方針について述べる.Sinnottの方法と同様に,問題の指数をいくつかの指数の積に分解して計算する.そこで重要なのは,l*を∞の上にある素点での付値が定めるK×からG=Gal(Km/k)の群環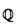 [G]への写像としたときの, [G]への写像としたときの, (1)l*(P)の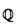 [G]のある部分群Uの中での指数[U:l*(P)]と, [G]のある部分群Uの中での指数[U:l*(P)]と, (2)指数[l*(P):l*(C)] の計算である.ここで(1)は,Sinnottの方法を少し変更することによってなされる.ここで定理の技術的な仮定が必要となる.(2)は可換図式を使って,HayesによるEmの指数の計算に帰着する. 以上のように本論文では,有限体上の関数体における,円単数の類似について,その階数,指数などの重要な不変量が一般の場合に計算されている.よって,論文提出者印林生は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. |