| 内容要旨 | | 次の問題を考える: 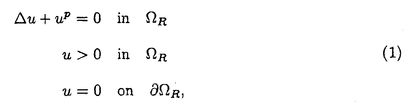 ここで R={x∈ R={x∈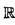 n|R-1<|x|<R+1}で,n>2の場合p∈(1,(n+2)/(n-2))そしてn=2の場合p∈(1,∞)とする. n|R-1<|x|<R+1}で,n>2の場合p∈(1,(n+2)/(n-2))そしてn=2の場合p∈(1,∞)とする. 上の問題(1)で領域が球の場合Gidas,NiおよびNirenbergの結果[Comm.Math.Phys.,1979]により解はすべて回転対称である. 円環領域 Rの場合でも同じ回転対称性を持っているので,このときも解は回転対称ではないかと考えられる.ところが,BrezisとNirenbergはn>2の場合(n+2)/(n-2)-pが正値で十分小さければ(1)の球対称でない解が存在することを示した[Comm.Pure Appl.Math.,1983]. Rの場合でも同じ回転対称性を持っているので,このときも解は回転対称ではないかと考えられる.ところが,BrezisとNirenbergはn>2の場合(n+2)/(n-2)-pが正値で十分小さければ(1)の球対称でない解が存在することを示した[Comm.Pure Appl.Math.,1983]. さらに,Coffmanはn=2の場合Rが大きくなるにつれて(1)のnonequivalentな回転非対称解の個数が無限大に近づくことを証明した[J.Differential Equations,1984].(ここで と と がnonequivalentであるというのは どんなg∈O(n)に対しても がnonequivalentであるというのは どんなg∈O(n)に対しても 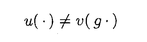 であることを意味する.)これは,球と円環は共に回転対称性を持っているのにもかかわらず,領域が球の場合は対称性が解集合の構造を単純にするように働き,領域が円環 Rの場合はRが大きくなるにつれて対称性が解集合の構造を複雑にするように働くことを示している.このような現象はn>3の場合でも起こることがY.Y.Liによって証明された[J.Differential Equations,1990]が,3次元の場合は同じ現象が起こるかどうか長い間未解決であった. Rの場合はRが大きくなるにつれて対称性が解集合の構造を複雑にするように働くことを示している.このような現象はn>3の場合でも起こることがY.Y.Liによって証明された[J.Differential Equations,1990]が,3次元の場合は同じ現象が起こるかどうか長い間未解決であった. 旧来の方法(即ち,n≠3の場合に用いられた方法)を焼き直してn=3の場合に適用する試みもなんとかなされたが成功しなかった.実は,後で述べるように旧来の方法はn=3の場合には適用できないことが本論文の結果から分かる.n=3の場合がn≠3の場合と比べると非常に異なることを説明するために,まずCoffmanとLiの旧来の戦略を紹介しよう. [Coffman,J.Differential Equations,1984]と[Li,J.Differential Equations,1990]におけるその証明の基本的戦略は次の最小化問題を考えることである: 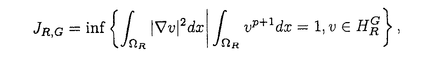 ここで, 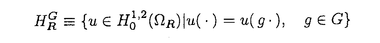 でGはO(n)の部分群であるとする.JR,Gのminimizerを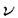 R,Gとすると, R,Gとすると, 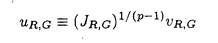 は(1)の解で,しかも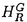 の中で最小エネルギーを持つ解である.Gkを角度 の中で最小エネルギーを持つ解である.Gkを角度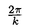 の回転によって生成される位数kのO(2)の部分群であるとし, の回転によって生成される位数kのO(2)の部分群であるとし,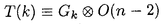 と定義する.Coffmanはn=2の場合,Liはn>3の場合,Rが十分大きければ と定義する.Coffmanはn=2の場合,Liはn>3の場合,Rが十分大きければ  であることを示した.これにより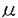 R,T(i)と R,T(i)と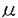 R,T(j)はnonequivalentになり,前述の結果を得る.しかし,n=3の場合,本論文[Theorem2.5]で述べているが十分大きいRに対し R,T(j)はnonequivalentになり,前述の結果を得る.しかし,n=3の場合,本論文[Theorem2.5]で述べているが十分大きいRに対し 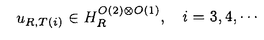 が成り立つ.したがって,  である.これはn≠3の場合とは非常に異なる現象である.ところで,これに関連した結果として,MizoguchiとSuzuki[preprint,1995]は任意のO(3)の部分群Gに対し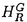 の中での最小エネルギー解 の中での最小エネルギー解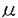 R,GとJR,GのRが無限大に近づく時の振る舞いを調べ, R,GとJR,GのRが無限大に近づく時の振る舞いを調べ, 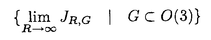 が有限集合であることを示している.しかし,本論文の結果のProposition2.4とTheorem2.5で用いられた方法で検証すると,彼らの結果をさらに精密化して,十分大きなRに対し  の個数は一様に有限であることが分かる.さらに 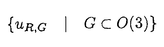 の中で互いに異なる対称性を持つものの数はRについて一様に有限である.このため,n=3の場合はn≠3の場合に用いられた旧来の戦略ではRが大きくなるにつれてnonequivalentな回転非対称解の個数が無限大に近づくかどうか分からない.旧来の方法の限界は,各部分空間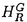 での最小エネルギー解のみを考察したことにある.そこで著者は,極小エネルギー解にも目を向けるとどうなるかを考えた.すなわち,部分空間 での最小エネルギー解のみを考察したことにある.そこで著者は,極小エネルギー解にも目を向けるとどうなるかを考えた.すなわち,部分空間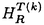 全体の上での最小化問題ではなく 全体の上での最小化問題ではなく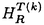 のある開集合での極小化問題を考えたわけである.通例の変分問題において,極小エネルギー解を探すのは,最小エネルギー解を探すよりもはるかに難しく,とくに(1)に関しては今まで考えられたことがなかった.著者は,空間的重みのついた制約条件を付加することで極小エネルギー解を求める方法を考案し,今まで知られていた解とは違う対称性を持つ解を見出すのに成功した.その結果を用いると,Rが無限大に近づくにつれて(1)のnonequivalentな回転非対称解の個数が無限大に近づくことが証明できる.次は本論文の主定理である. のある開集合での極小化問題を考えたわけである.通例の変分問題において,極小エネルギー解を探すのは,最小エネルギー解を探すよりもはるかに難しく,とくに(1)に関しては今まで考えられたことがなかった.著者は,空間的重みのついた制約条件を付加することで極小エネルギー解を求める方法を考案し,今まで知られていた解とは違う対称性を持つ解を見出すのに成功した.その結果を用いると,Rが無限大に近づくにつれて(1)のnonequivalentな回転非対称解の個数が無限大に近づくことが証明できる.次は本論文の主定理である. Theorem.l>1を満たす任意の整数lに対し正定数Rlが存在して,R>Rlのとき (1)の互いにnonequivalentな回転非対称解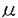 R,2,…, R,2,…,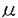 R,lが存在して次を満たす: R,lが存在して次を満たす: (1)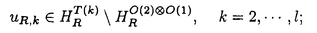 (2)任意のk∈{2,…,l}に対し,Rが無限大に近づくとき, 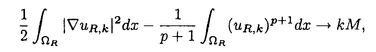 ここでMはkに依存しないある定数. |
| 審査要旨 | | 論文提出者 卞 在瑩は,3次元円環領域上の半線形楕円型方程式を考察し,異なる対称性をもつ数多くの解の存在を変分法を用いて証明した.この結果により,n次元の問題に対するある予想について,唯一未解決のまま残っていた3次元の場合が解決された. 論文提出者が考察したのは,以下の半線形楕円型方程式に対する境界値問題である。 ここでは,いわばn次元の円環領域であり,指数pについては,通例よく行なわれるように1<p<(n+2)/(n-2)という仮定をおくものとする. 上の問題(1)で領域 Rを球で置き換えた場合には,Gidas,NiおよびNirenbergの結果[Comm.Math.Phys.,1979]により,解はすべて回転対称であることが知られている.これに対し,円環領域 Rを球で置き換えた場合には,Gidas,NiおよびNirenbergの結果[Comm.Math.Phys.,1979]により,解はすべて回転対称であることが知られている.これに対し,円環領域 Rの場合には,球と同じO(n)対称性を持つにも関わらず,その対称性が必ずしも解に遺伝しないことがBrezisとNirenbergにより発見された[Comm.Pure Appl.Math.,1983]. Rの場合には,球と同じO(n)対称性を持つにも関わらず,その対称性が必ずしも解に遺伝しないことがBrezisとNirenbergにより発見された[Comm.Pure Appl.Math.,1983]. さらに,Coffmanは,n=2の場合R→∞とすると(1)の互いに「同値でない」解の個数が限りなく大きくなることを証明した[J.Differential Equations,1984].(ここで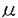 と と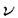 が「同値でない」とは,任意のg∈O(n)に対して が「同値でない」とは,任意のg∈O(n)に対して が成り立つことを意味する.)同様の現象はn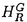 4の場合にも起こることがY.Y.Liによって証明された[J.Differential Equations,1990]が,3次元の場合に同じ現象が起こるかどうかは長らく未解決であった. 4の場合にも起こることがY.Y.Liによって証明された[J.Differential Equations,1990]が,3次元の場合に同じ現象が起こるかどうかは長らく未解決であった. 上の境界値問題を変分法によって定式化すると,その解が次の汎関数(以下「エネルギー」と呼ぶ)の臨界点として得られることはよく知られている. CoffmanやLiがn≠3の場合に用いた方法は,次のようなものであった.まず,O(n)のさまざまな部分群Gに対して,G-不変な関数のなす部分空間 を考える.この部分空間上でエネルギーJRを最小化する点をを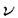 R,Gとすると, R,Gとすると, が(1)のG-不変な解になることはすぐわかる.CoffmanとLiは,臨界値の集合 がR→∞のときに無限大に発散することをn≠3の場合に確かめ,これから,(1)の互いに同値でない解の個数がR→∞のとき限りなく大きくなることを導いた. これに対し論文提出者は,n=3の場合は上記の臨界値の個数がR→∞のとき有界にとどまることを示し,よって旧来の方法では解の同値類の個数がR→∞のとき無限大に発散するかどうかを確かめられないことを明らかにした. 旧来の方法の限界は,各部分空間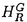 での最小エネルギー解のみを考察したことにあると看破した論文提出者は,次に,極小エネルギー解にも目を向けるとどうなるかを考えた.すなわち,部分空間 での最小エネルギー解のみを考察したことにあると看破した論文提出者は,次に,極小エネルギー解にも目を向けるとどうなるかを考えた.すなわち,部分空間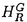 全体の上での最小化問題ではなく 全体の上での最小化問題ではなく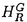 のある開集合での極小化問題を考えたわけである.通例の変分問題において,極小エネルギー解を探すのは,最小エネルギー解を探すよりもはるかに難しく,とくに(1)に関しては今まで考えられたことがなかった.論文提出者は,空間的重みのついた制約条件を付加することで極小エネルギー解を求める方法を考案し,今まで知られていた解とは異なる対称性を持つ解を見出すのに成功した.その結果を用いると,Rが無限大に近づくにつれて(1)の互いに同値でない回転非対称解の個数が無限大に発散することが証明でき,これにより,はじめに述べた未解決問題が肯定的に解決できたのである. のある開集合での極小化問題を考えたわけである.通例の変分問題において,極小エネルギー解を探すのは,最小エネルギー解を探すよりもはるかに難しく,とくに(1)に関しては今まで考えられたことがなかった.論文提出者は,空間的重みのついた制約条件を付加することで極小エネルギー解を求める方法を考案し,今まで知られていた解とは異なる対称性を持つ解を見出すのに成功した.その結果を用いると,Rが無限大に近づくにつれて(1)の互いに同値でない回転非対称解の個数が無限大に発散することが証明でき,これにより,はじめに述べた未解決問題が肯定的に解決できたのである. 論文提出者の考案した手法は,非常に巧妙で,この問題に限らず他にさまざまな応用があると思われる.実際,論文提出者は,類似の方法を用いて,特異摂動領域における境界値問題の解の構造についてのN.Dancerの予想の解決に成功している.このように,提出論文は,得られた結果そのものの価値に加えて,そこで開発された手法も,高い重要性を有している. 以上の諸点を考慮した結果,論文提出者卞在瑩は,博士(数理科学)の学位を受けるにふさわしい十分な資格があると認める. |