申請者は本論文で3次元リーマン多様体Nの中で与えられた平均曲率をもつ曲面が存在するための条件をNの幾何学的な情報で記述することに成功した。 基本的な問題は下記のように定式化される。 問題「Mを閉曲面、Nを3次元の向き付けられたリーマン多様体とする。MからNへの写像の自由ホモトピークラス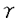 を与えたとき、Mの上の複素構造cと を与えたとき、Mの上の複素構造cと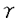 に属する写像uであって、cについてuが下記の方程式を満たすようなものがあるか? に属する写像uであって、cについてuが下記の方程式を満たすようなものがあるか? ただし、方程式の微分はcと共形的な計量に関するものとし、▽iuは局所正規直交標構に関する微分、×はNの体積要素volから〈X,Y×Z〉=vol(X,Y,Z)で定まるテンソルとする。」 申請者はまず上記の問題が変分問題として定式化できることを示した.まず、複素構造を固定して与えられたリーマン面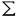 の上で方程式(1)について考える。 の上で方程式(1)について考える。 u0∈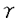 を一つ固定する。u∈ を一つ固定する。u∈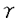 に対して汎関数IH(・,u0)を下記のように定める。 に対して汎関数IH(・,u0)を下記のように定める。 ここでfはu0とuを結ぶホモトピーである。すなわち、fは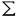 ×[0,1]からNへの写像であり、f(・,0)=u0(・)f(・,1)=u(・)を満たすものである。 ×[0,1]からNへの写像であり、f(・,0)=u0(・)f(・,1)=u(・)を満たすものである。 まず申請者は,この汎関数はfのとり方に依存して定義されたが,Nが負曲率を持つときはfのとり方には依らずに定まることを示し,方程式(1)はIH(・,u0)のオイラー・ラグランジュ方程式になっていることをしめした. 申請者は,方程式(1)の解の存在について下記を示した。 定理A 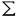 を閉リーマン面、Nを断面曲率が上から-K2で押さえられ、単射半径が一様に下から押さえられているような完備3次元リーマン多様体とする。このとき、|H|<Kならば、IHを最小にする方程式(1)の解が存在する。 を閉リーマン面、Nを断面曲率が上から-K2で押さえられ、単射半径が一様に下から押さえられているような完備3次元リーマン多様体とする。このとき、|H|<Kならば、IHを最小にする方程式(1)の解が存在する。 次に、複素構造も変分して、方程式(2)まで含めた解の存在を考える。この場合の変分問題への帰着は、方程式(1)を前提にすれば古典的に知られ、下記のようにすればよい。 「Mを底曲面とするタイヒミュラー空間の元p=[(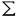 ,S)]( ,S)](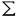 はリーマン面、SはMから はリーマン面、SはMから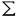 への位相同型)に対し、 への位相同型)に対し、 の値を対応させることにより、タイヒミュラー空間上の汎関数IH(・,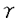 )が定義される。この汎関数の最小値に対応する複素構造と方程式(1)の解の組(これは、定理Aによりかならず存在する。)は方程式(2)を満たす。」 )が定義される。この汎関数の最小値に対応する複素構造と方程式(1)の解の組(これは、定理Aによりかならず存在する。)は方程式(2)を満たす。」 申請者は下記の定理を示した。 定理BNおよびHは定理Aと同じ仮定を満たすものとする。さらに、Mの種数は2以上とし、ホモトピークラス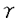 は基本群に単射を誘導するものとする。このとき、IH(・, は基本群に単射を誘導するものとする。このとき、IH(・,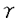 )は最小点を持ち、対応する複素構造と方程式(1)の解の組は、方程式(1)および(2)をみたし、その解は分岐はめ込みとなる。さらにHとNが実解析的ならば、はめ込みとなる。 )は最小点を持ち、対応する複素構造と方程式(1)の解の組は、方程式(1)および(2)をみたし、その解は分岐はめ込みとなる。さらにHとNが実解析的ならば、はめ込みとなる。 また、NがS1作用を持つような場合、ある位相的な条件によって解が存在しない場合があることを示した。(定理C)特に、これはフラットトーラスの場合も含み、定理AおよびBにおいて負曲率の条件が落とせないことも示している。また、定理Bの条件がcriticalな時、すなわちH≡1でNが双曲的なときはBryant,Umehara-Yamadaなどにより研究されているCMC1曲面に一致するが、その場合の安定性についても論じた。(命題D) さて上述の基本問題の特別な場合は多くの先人の研究の蓄積がある.すなわちH=0の場合,方程式(1)はいわゆる調和写像の方程式であり,方程式(2)を加えると極小曲面の方程式となる.この場合に上記の定理(A),(B)は良く知られた処である. 一方Nがユークリッド空間の場合はいわゆるR3の中のH-systemの研究と深い関連がある。この場合はDirichlet問題が研究対象であり,直接の関係はないがそこで得られた局所的結果と用いられた等周不等式の手法は申請者に上記基本問題の解決に本質的に役にたっている.すなわち申請者は等周不等式を下記のように拡張した.任意の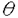 ∈(0,1)に対して定数C(K, ∈(0,1)に対して定数C(K,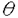 )が存在して )が存在して が成り立つ. この一般化された等周不等式により上述の変分問題は,解析的にはいわばH=0と同じ取り扱いができることを申請者は看破することにより,調和写像,極小曲面,R3の中のH-systemの研究成果を巧みに組み合わせることにより本論文の結果を得た. 申請者は本論文において大域解析学で興味ある問題に独創的な考察を行うことにより重要な結果を得た.よって論文提出者戸田正人は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. |