| 内容要旨 | | 量子コホモロジー環とグロモフ・ウイッテン母関数の満たす微分方程式 複素ケーラー多様体Vに対し、グロモフ・ウイッテン不変量は、ある種の公理系を満たす線形関数の族 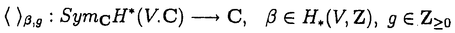 であり、特に種数g=0の不変量はH*(V,C)に量子コホモロジー環の構造を定める。複素ケーラー形式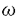 と、H*(V,C)のC基底 と、H*(V,C)のC基底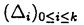 を一つとり、グロモフ・ウイッテン不変量の母関数を を一つとり、グロモフ・ウイッテン不変量の母関数を 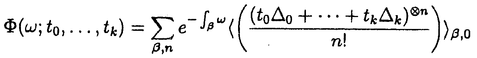 で定める。このグロモフ・ウイッテン不変量の母関数について研究し、この母関数が、量子コホモロジー環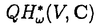 の定義イデアルから定まる微分方程式を満たすことを示した。また、トーリック多様体に対して相関関数の計算を行った。 の定義イデアルから定まる微分方程式を満たすことを示した。また、トーリック多様体に対して相関関数の計算を行った。 トーリック多様体の量子コホモロジー環と相関関数 階数kの自由Z加群Nの扇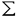 に対応するトーリック射影多様体 に対応するトーリック射影多様体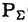 の量子コホモロジー環 の量子コホモロジー環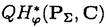 は、バチレフ氏によりその構造が決定されている。さらに、Nの双対Z加群の基底 は、バチレフ氏によりその構造が決定されている。さらに、Nの双対Z加群の基底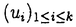 をとり、対応する(CX)kの座標を をとり、対応する(CX)kの座標を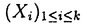 としたとき、 としたとき、 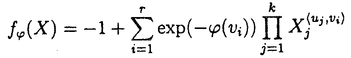 で定まる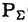 の中のカラビ・ヤウ超曲面 の中のカラビ・ヤウ超曲面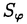 を考える。ここで、v1,…,vrは扇 を考える。ここで、v1,…,vrは扇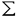 の一次元錐の原始生成元であり、 の一次元錐の原始生成元であり、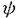 はNR上のC値R線形関数で複素ケーラー類に対応している。このとき、 はNR上のC値R線形関数で複素ケーラー類に対応している。このとき、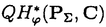 は、 は、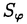 のヤコビアン環と同形であることが知られている。 のヤコビアン環と同形であることが知られている。 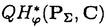 はviに対応する二次コホモロジー類 はviに対応する二次コホモロジー類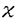 iで生成されているので、 iで生成されているので、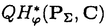 の元は多項式P( の元は多項式P(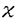 1,…, 1,…,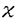 r)で表される。このとき、相関関数 r)で表される。このとき、相関関数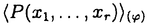 がカラビ・ヤウ超曲面の定義方程式 がカラビ・ヤウ超曲面の定義方程式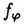 を用いて、 を用いて、 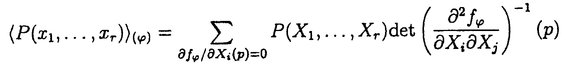 と表されることを示した。これは、グラスマン多様体に対して知られているバッファ・イントリリゲイターの公式の類似となっている。 樹木オペラッド上の代数に付随した形式群 オペラッドは場の理論を代数的に取り扱うための重要な構造であるが、特に樹木オペラッドTは点付き有理曲線のモジュライ空間の構造とも関係があり幾何学的にも興味深い。この樹木オペラッド上の代数Vとは、ある体k上の有限次元ベクトル空間であって、オペラッドの準同形 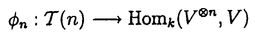 が定められているものである。kの標数が0のとき、このVに対して形式群を次のように定義する。まず、Vのk基底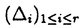 に対応する変数 に対応する変数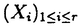 を導入し、 を導入し、 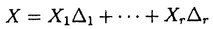 とする。次に、母関数E(X)を 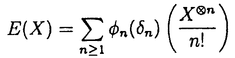 で定義する。ここで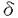 nはn-カローラである。これを用いて、r次元形式群がつぎのFで与えられる。 nはn-カローラである。これを用いて、r次元形式群がつぎのFで与えられる。 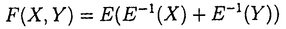 これにより、r次元形式群とV上のT代数の構造が一対一に対応することが示され、Q上のr次元普遍形式群とr次元T普遍代数との対応も解る。 また、VがWDVV代数となるための条件や、ダブロービン接続とE(X)を対数に持つような形式群Fvとの関係について調べた。 |
| 審査要旨 | | 量子コホモロジー環は1990年代になってケーラー多様体の位相的シグマモデルの考察から物理学者によって導入された斬新な概念である.これは、複素ケーラー多様体Vに対して定義されたGromov-Witten不変量をもちいてVのコホモロジー群H*(V,C)に新しい環構造をさだめたものである.RuanとTianは半正値対称多様体Vに対しGromov-Witten不変量を構成しそれを用いてVの量子コホモロジー環の構造を与えた.一方,KontsevichとManinはGromov-Witten不変量を公理的に定義し,それにもとずいて量子コホモロジー環の一般論を展開した.論文提出者前野俊昭の博士論文は3部からなり,これらの成果をふまえて量子コホモロジー環の構造をさらに分析したものである. 第1部では,Gromov-Witten不変量の母関数の特徴付けの問題を扱っている.そのために,Kontsevich-Maninの理論を整理し,この母関数が従来知られていた非線形偏微分方程式であるWDVV方程式を満たすばかりか,量子コホモロジー環の定義イデアルから定まる線形微分方程式系をもみたすことを示した.また逆に,適当な初期条件の下に,この母関数がこれらの微分方程式達で特徴付けられることをしめした.さらに,この理論をトーリック多様体に応用し,トーリック多様体の相関関数が満たす微分方程式系が超幾何方程式の類似になっていることをあきらかにした. 第2部では,トーリック多様体の相関関数を局所的なデータで記述する公式を与えている.階数kの自由Z加群Nの扇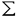 に対応するトーリック多様体を に対応するトーリック多様体を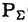 とする.Nの双対Z加群の基底u1,u2,…,ukをとり,対応する(C*)kの座標をX1,X2,…,Xkとする.v1,v2,…,vkを扇 とする.Nの双対Z加群の基底u1,u2,…,ukをとり,対応する(C*)kの座標をX1,X2,…,Xkとする.v1,v2,…,vkを扇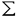 の一次元錐の原始生成元とし, の一次元錐の原始生成元とし,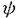 を複素ケーラー類に対応するR線形関数とする.このとき,多項式で与えられるCalabi-Yau多様体S を複素ケーラー類に対応するR線形関数とする.このとき,多項式で与えられるCalabi-Yau多様体S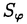 を考えれば,トーリック多様体 を考えれば,トーリック多様体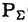 の量子コホモロジー環は の量子コホモロジー環は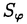 のJacobi環として与えられることがBatyrevにより示されている.においてviに対応する二次コホモロジー類を のJacobi環として与えられることがBatyrevにより示されている.においてviに対応する二次コホモロジー類を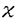 iとすれば,の元P( iとすれば,の元P(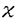 1, 1,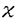 2,…, 2,…,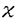 r)に対応する相関関数を得る.論文提出者はこの相関関数が r)に対応する相関関数を得る.論文提出者はこの相関関数が と表示されることを示した.これはグラスマン多様体に対するVafa-Intriligatorの公式のトーリック多様体版になっており,大変美しい結果である. オペラッドは弦の場の量子論を記述する際に重要な役割を演じる.n点付の種数0の安定曲線のモジュライ空間を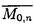 とすれば,オペラッドを得る.それは,にオペラッドの構造を誘導する.多様体のコホモロジー群の上に代数の構造,すなわちWDVV代数の構造が与えられていれば,その代数の構造はWDVV方程式の解によって与えられることが知られている.第3論文においては,論文提出者は標数0の体上のr次元ベクトル空間Vの樹木オペラッド代数の構造に対してr次元可換形式群が構成できることを示した.その際,普遍的な樹木オペラッド代数の構造に対しては普遍的な可換形式群が構成できることがわかる.また,樹木オペラッド代数がWDVV代数になるための必要十分条件をある形式群上のベクトル場の空間の接続と不変微分形式の言葉で与えた。 とすれば,オペラッドを得る.それは,にオペラッドの構造を誘導する.多様体のコホモロジー群の上に代数の構造,すなわちWDVV代数の構造が与えられていれば,その代数の構造はWDVV方程式の解によって与えられることが知られている.第3論文においては,論文提出者は標数0の体上のr次元ベクトル空間Vの樹木オペラッド代数の構造に対してr次元可換形式群が構成できることを示した.その際,普遍的な樹木オペラッド代数の構造に対しては普遍的な可換形式群が構成できることがわかる.また,樹木オペラッド代数がWDVV代数になるための必要十分条件をある形式群上のベクトル場の空間の接続と不変微分形式の言葉で与えた。 本論文はこのように,世界で現在もっとも活発に研究されているテーマの1つをとりあげ,新しい構造と概念の発見を行いまとめあげたすぐれたものである.よって、論文提出者 前野 俊昭は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |