| 内容要旨 | | グラフGがperfect graph(「理想グラフ」と訳される)であるとは、Gの任意の点部分グラフHが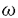 (H)-彩色可能である時を言う。グラフGの隣接していない2点対(x,y)がcritical non-edgeであるとは、 (H)-彩色可能である時を言う。グラフGの隣接していない2点対(x,y)がcritical non-edgeであるとは、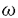 (G+xy)> (G+xy)>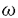 (G)が成立する時を言う。ただしここで、G+xyとはGに枝xyを付加したグラフのことであるとする。Gの極大なstable set Sがforced color classであるとは、SがGのすべての (G)が成立する時を言う。ただしここで、G+xyとはGに枝xyを付加したグラフのことであるとする。Gの極大なstable set Sがforced color classであるとは、SがGのすべての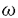 -cliquesと交わり、かつ、Gのcritical non-edgesの内で、その両端点が共にSに含まれている様なものだけを全て集めて -cliquesと交わり、かつ、Gのcritical non-edgesの内で、その両端点が共にSに含まれている様なものだけを全て集めて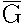 の部分グラフを作った時に、そのグラフがただ1つの連結成分を持つ時を言う。Gの枝がdeterminedであるとは、Gのある1つの の部分グラフを作った時に、そのグラフがただ1つの連結成分を持つ時を言う。Gの枝がdeterminedであるとは、Gのある1つの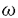 -cliqueが、その両端点を同時に含んでいる時を言う。 -cliqueが、その両端点を同時に含んでいる時を言う。 Strong Perfect Graph Conjecture(理想グラフに関する強い予想)とは、「極小な非理想グラフは弦を持たない5点以上の奇数点サイクルとその補グラフに限られるであろう。」という予想であり、著名なグラフ理論家C.Berge[1]が1961年にこれを提起して以来、殊にいわゆる四色予想が肯定的に解決された現在においては、グラフ理論において解決が待たれる最も重要な予想の1つに数えられているが、同時に極めて困難な問題であることも知られ、幾つかのグラフの族について肯定的に解かれてはいるものの、一般のグラフについての完全な形での解決の目度は未だ立っていないのが現状である。 極小な非理想グラフから任意の1点を除去すると、一意彩色可能な理想グラフとなる。S.E.Markosian等(1986年)は、一意彩色可能な理想グラフに特徴的に見受けられるcritical non-edgeや、forced color classといった組合せ構造を調べ、極小な非理想グラフ上でのこれらの組合せ構造と、Strong Perfect Graph Conjectureとの関係を論じた。その後この結果はG.Bacso(1989年)やG.Bacso(1993年)、J.Fonlupt and A.Sebo[2]、A.Sebo[5,6]等によって詳細に研究が進められ、極小な非理想グラフに、いくつかの自然な組合せ論的構造の存在を仮定すれば、Strong Perfect Graph Conjectureもまた成立することが、次々と明らかにされて来たのである。 まず1993年には、それまでの諸結果を集約する形で、G.Bacsoにより、Strong Perfect Graph Conjectureを含むより強い予想として以下のような予想が提起された。すなわち、「もしGが一意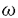 彩色可能な理想グラフであるならば、Gは少なくとも1つのforced color classを有するであろう」というものである。この予想は、Bold Conjectureと呼ばれ、広く知られている。(なおその詳細については[3]を見られたい。) 彩色可能な理想グラフであるならば、Gは少なくとも1つのforced color classを有するであろう」というものである。この予想は、Bold Conjectureと呼ばれ、広く知られている。(なおその詳細については[3]を見られたい。) さらにこれに関連して極最近、A.Sebo[6]によって、「任意の1つの極小な非理想グラフGについてG-pが少なくとも1つのforced color classを有する様にp∈V(G)を取ってくることが常に可能であるならば、Strong Perfect Graph Conjectureもまた、正しい」ということが示された。続いて彼は重要な問題提起であると前置きした上で、実質的にはG.BacsoのBold Conjectureの成立の可否を改めて問うている。すなわち、(1):「自分およびその補グラフが持つ、すべての一意彩色可能な点部分グラフが、それぞれ少なくとも1つのforced color classを有するようなグラフの族を取れば、その上ではStrong Perfect Graph Conjectureは成立している訳であるが、これはすべてのグラフの族について成立する様な普遍的な性質なのではないだろうか?」 Sebo[6]は、さらに踏み込んで極小な理想グラフの性質に関連する幾つかの結果を得た上で、以下のような2つの予想をも提起しているが、これらの予想はいずれもStrong Perfect Graph Conjectureが正しければ、同時に成立する。すなわち、(2):「極小な非理想グラフGが2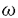 (G)-2本のdeterminedな枝と接続しているような点pを持ち、かつその補グラフ (G)-2本のdeterminedな枝と接続しているような点pを持ち、かつその補グラフ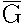 もまた2 もまた2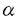 (G)-2本のdeterminedな枝と接続しているような点qを有しているならば、Gは弦を持たない5点以上の奇数点サイクルであるか、もしくはその補グラフである。」という予想、および(3):「極小な非理想グラフGの点 (G)-2本のdeterminedな枝と接続しているような点qを有しているならば、Gは弦を持たない5点以上の奇数点サイクルであるか、もしくはその補グラフである。」という予想、および(3):「極小な非理想グラフGの点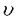 およびこれを含む2つの およびこれを含む2つの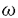 -cliquesAとBがあって、 -cliquesAとBがあって、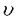 を含む様なGのすべての を含む様なGのすべての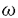 -cliquesが、常にA∪Bによって被覆されているならば、Gは弦を持たない5点以上の奇数点サイクルであるか、もしくはその補グラフである。」という予想である。 -cliquesが、常にA∪Bによって被覆されているならば、Gは弦を持たない5点以上の奇数点サイクルであるか、もしくはその補グラフである。」という予想である。 本論文では、まず第1に、Bold Conjectureはもとより、それに含まれるようなより弱い予想に対してさえ具体的な反例を構成することが出来ることを示して、Bold Conjectureを否定的に解決する。(そうしてこの結果はまた、(1)に対する直接の解答を明示している。) 第2に、「極小な非理想グラフGが2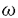 (G)-2本のdeterminedな枝と接続しているような点pを持ち、かつその補グラフ (G)-2本のdeterminedな枝と接続しているような点pを持ち、かつその補グラフ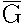 もまた2 もまた2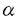 (G)-2本のdeterminedな枝と接続しているような点qを有しており、かつ(p,q)がGもしくは (G)-2本のdeterminedな枝と接続しているような点qを有しており、かつ(p,q)がGもしくは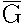 のdeterminedな枝であるならば、Gは弦を持たない5点以上の奇数点サイクルであるか、もしくはその補グラフである。」ことを示す。これは(2)の部分的な解決を意味する。さらに第3として、「極小な非理想グラフGが2K2-freeであり、かつ のdeterminedな枝であるならば、Gは弦を持たない5点以上の奇数点サイクルであるか、もしくはその補グラフである。」ことを示す。これは(2)の部分的な解決を意味する。さらに第3として、「極小な非理想グラフGが2K2-freeであり、かつ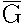 のすべての枝はdeterminedであるとする。ここで、Gの点 のすべての枝はdeterminedであるとする。ここで、Gの点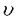 およびこれを含む2つの およびこれを含む2つの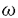 -cliquesAとBがあって、 -cliquesAとBがあって、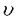 を含む様なGのすべての を含む様なGのすべての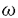 -cliquesが、常にA∪Bによって被覆されているならば、Gは弦を持たない5点以上の奇数点サイクルの補グラフである」ことを証明する。これは(3)を部分的に解決したことを意味する。なおここで、4点で構成されるグラフFを禁止グラフとする、F-freeグラフの族の内では、2K2-freeなグラフの族(あるいは同じことであるが、その補グラフとしてのC4-freeなグラフの族)に対してのみ、未だ「Strong Perfect Graph Conjectureが成立するか否か」が証明されていないという事実をもここに指摘しておきたい。 -cliquesが、常にA∪Bによって被覆されているならば、Gは弦を持たない5点以上の奇数点サイクルの補グラフである」ことを証明する。これは(3)を部分的に解決したことを意味する。なおここで、4点で構成されるグラフFを禁止グラフとする、F-freeグラフの族の内では、2K2-freeなグラフの族(あるいは同じことであるが、その補グラフとしてのC4-freeなグラフの族)に対してのみ、未だ「Strong Perfect Graph Conjectureが成立するか否か」が証明されていないという事実をもここに指摘しておきたい。 参考文献[1]C.Berge,Farbung von Graphen,deren samtliche bzw.deren ungerade Kreise starr sind,Wiss.Z.Martin Luther Univ.Halle-Wittenberg 10(1961),114-115.[2]J.Fonlupt and A.Sebo,On the clique-rank and the coloration of perfect graphs,in:Integer Programming and Combinatorial Optimization volume 1,(eds.R.Kannan and W.R.Pulleyblank),University of Waterloo Press,Waterloo(1990),201-216.[3]T.R.Jensen and B.Toft,Graph Coloring Problems,John Wiley & Sons,New York(1995).[4]S.E.Markosian,G.S.Gasparian,A.S.Markosian,On a conjecture of Berge,J.Combin.Theory B 56(1992),97-107.[5]A.Sebo,Forcing Colorations and the Perfect Graph Conjecture,in:Integer Programming and Combinatorial Optimization volume 2,(eds.E.Balas,G.Cornuejols and R.Kannan),Mathematical Programming Society and Carnegie Mellon University(1992),353-366.[6]A.Sebo,On critical edges in minimal imperfect graphs,J.Combin.Theory B 67(1996),62-85. |
| 審査要旨 | | 平面グラフの彩色数を定める四色問題は、つとに世評に有名な問題であった。この四色問題が解決を見た現在、グラフ理論における最大の課題となる問題を挙げれば、グラフの再構成問題と強理想グラフ予想になるであろう。 理想グラフとは、その任意の誘導部分グラフ上でクリーク数が彩色数に、及び安定数がクリーク被覆数にそれぞれ等しくなるグラフのことである。ここで長さ5以上の奇数長のサイクルとその補グラフは、理想グラフにならない自明な例であるが、極小な非理想グラフはこれらにかぎられる、というのがC.Bergeによる強理想グラフ予想である。 理想グラフに関連してこれまでに、L.Lovaszによる弱理想グラフ定理の証明に始まって、分割可能グラフの特徴付け、V.Chvatalによる独立多面体の整数性による理想グラフの特徴付け、また区間グラフ、三角化グラフなどの特殊な理想グラフのクラスの研究などが精力的に行われてきた。この中で、論文提出者は極小非理想グラフの性質を明らかにし、それを特徴づけることにより、直接的に強理想グラフ予想を解決する方向で研究を行った。その過程で、安定数、クリーク数と強く結びついたcritical枝、critical非枝という概念、その存在が安定数、クリーク数に何の影響も及ぼさない枝であるweak枝という概念を導入しその考察を端緒に研究を進めた。critical枝に関しては独立にS.E.Markosianらによる先駆的研究もある。極小非理想グラフを直接に特徴づける方向の研究では、これらの概念が現在重要な手段になっている。 論文提出者は、これらの特殊な枝の存在条件や配置を調べることで、いくつかの付加条件の下であれば極小な非理想グラフが奇数長のサイクルかその補グラフになり、強理想グラフ予想が成立することを示した。ここでの付加条件を一般に非理想グラフが満たすことを示せれば、理想グラフ予想の最終的解決に至る。 極小な非理想グラフから1点を除くと、一意彩色可能理想グラフになることはよく知られており、これから一意彩色可能理想グラフの性質について理想グラフ予想の研究の面から詳しく調べられている。 critical枝が1つの彩色点集合を張るとき、これは強制彩色集合と呼ばれる。これまでの研究の成果から、自然な推論として「一意彩色可能理想グラフは強制彩色集合をもつ」と考えられて、これをG.BacsoがBold予想と名付けた。この予想はこれまでの様々な予想に関連しており、肯定的に解決されることが強く期待されていた。これに対して、論文提出者はこのBold予想に反例を構成する事に成功し、これを否定的に解決した。この反例は24点からなる比較的大きなグラフである。ここから一意彩色可能な理想グラフの構造を明らかにして理想グラフ予想に迫ろうというアプローチが、現在の形のままでは不首尾であることを明らかにした。この反例は、すでに当該専門分野の情報を集めたインターネットのWWWサイトのいくつかに掲示され、広く知られるところとなっている。 強理想グラフ予想自身は難問であるため、制限をつけた形で予想を解こうという試みがいくつかなされている。その中に、極小な非理想グラフにおいてdetermined枝がある付加的な条件を満たせば、それは奇数長のサイクル又はその補グラフになるであろうというA.Seboによる予想がある。さらに同時に、極小非理想グラフがそのような付加的な性質を常に持つことを示せれば、理想グラフ予想を肯定的に解決することになるが、本論文提出者はこれを部分的に解決し、極小非理想グラフ中にweakペアと呼ばれる特殊な枝が存在しなければSeboによるこの予想が成立することを示した。このweakペアについては、極小非理想グラフ中には存在しないと強く一般に推察されているので、この推察が最終的に正しいと分かれば、論文提出者の結果とあわせることにより、理想グラフ予想が解決されることになる。 別に、極小非理想グラフに存在することが期待されるもう一つの構造としてlocal semi-web structureと呼ばれるある特殊なクリーク族の構造がある。これについて、極小非理想グラフがlocal semi-web structureを持つとすれば、それは奇数長のサイクル又はその補グラフになるだろうという予想があり、これに対して本論文提出者は、本質的にC4-freeなグラフではこの予想が成立することを示し、部分的な解決を与えた。 以上要するに論文提出者は強理想グラフ予想という現在のグラフ理論の難問に正面から取り組み、その極小非理想グラフが持つ性質について重要な知見をもたらした。この提出論文の第一部は、提出者の単著論文として学術論文誌に掲載予定である。また第二部は国際シンポジウムで単著で発表済みで、そこでも高い評価を得ている。 よって本論文は博士(学術)の学位請求論文として合格と認められる。 |