ポアソン方程式,移流拡散方程式等の偏微分方程式は有限要素法,差分法等により離散化を行ない大規模な疎行列を係数とする連立一次方程式の解法に帰着される.この疎行列の解法にはガウスの消去法,ガウス-ジョルダン等の直接解法とマルチグリッド(MG)法、共役勾配(CG)法,SOR法等の反復解法があるが,偏微分方程式を離散化してできた行列は比較的条件が良いため,一般には直接法より収束効率の良い反復解法を用いた方が解を速く求めることが出来る.本研究では良い収束率を持ちかつ高い並列性を持つ反復解法の研究として,反復解法のマルチグリッド法と前処理付き共役勾配法の二つを組み合わせ,CG法の前処理としてMG法を用いるマルチグリッド前処理付き共役勾配(MGCG)法の提案を行ない,その収束率の評価および並列計算機への効率的な実装の研究を行なう.

　共役勾配法の前処理としては、対称で正定値であることが十分条件である.従って,この条件を満たすためのMG法の十分条件を求める必要がある.まず,MG法の最も簡単な場合である2グリッド法を考える.2グリッド法のプレスムージングしか行なわない場合は,スムージング法に減速(damped)リチャードソン法の様な前処理行列,反復行列がともに対称な解法を用い,かつ共役勾配法の内積としてN-energy内積を用いることが十分条件であることを証明した.ここでN＝H^2m,Hはスムージング法の反復行列,2mはその反復回数である.またプレスムージング,ポストスムージングの両方を行なう場合,ポストスムージング法にプレスムージング法と対称(adjoint)な解法を用い,収束する(反復行列のスペクトル半径が1より小さい)ことが十分条件であることを証明した.次に,MG法に対しての十分条件を求めた.Vサイクルの場合は2グリッド法のいずれかの条件を各グリッドで満たせば良く,Wサイクルあるいはそれ以上のサイクルの場合は,各グリッドでのVサイクルのマルチグリッド法が収束することがその十分条件であることを証明した.このことによりこれらの条件を満たすMG前処理を行なったCG法の収束性を証明することができる.

　次に,このMGCG法の収束率の解析を行なう.これまでの研究ではCG法の収束率の解析は係数行列の固有値分布によることが分かっている.またMG法の収束率の解析ではスムージング法による短波長成分のスムージング特性,粗いグリッドによる残差の修正を表す近似特性を評価することにより解析を行なっているが,MGCG法はCG法の前処理にMG法を用いるものであるため,MGCG法の収束率の解析を精密に行なうためにはMG前処理後の行列の固有値分布を求める必要があり,本研究では1次元,2次元の拡散係数一定のポアソン方程式をモデル問題とし,減速ヤコビ法,レッドブラックガウスザイデル(RB-GS)法をそれぞれスムージング法としたMGCG法の解析を行なった.各グリッドにおけるフーリエモードを使うことにより,MG前処理後の行列の全ての固有値を解析的に求めることができ,その結果,1次元の場合はRB-GS法をスムージング法としたMG法は1反復で厳密解を与え,減速ヤコビ法を用いたMGCG法は減速ファクター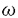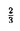＝の時に2反復で厳密解を与えることがわかった.また2次元の場合は、孤立固有値はなくほぼ連続的であったため固有値の区間によるMGCG法の収束率の評価が非常に良い評価を与え,減速ヤコビ法を用いたMGCG法の収束ファクター(誤差の減少率)は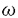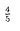＝の時0.111,RB-GS法を用いた場合は0.0718であることがわかった.つまりRB-GS法を用いたMGCG法は14回反復すれば相対誤差は10^-16以下になるということである.MG法と比べた場合,MGCG法の反復回数はほぼMG法の半分となり,MGCG法一反復に必要な演算量はMG法の一反復の1.5倍以下であるため、MGCG法の方が優れていることになる.原理的にはこの2グリッド前処理で行なった解析手法をMG前処理に拡張することは可能であるが,非常に繁雑になってしまうためMG前処理後の行列の固有値は数値実験で求めた.その結果,グリッドレベルを増やしていくとわずかながら収束率が悪くなることが分かった.しかしながら,これはまだ示せていないがその下限は2グリッド前処理のわずか下であることが期侍される.

　以上の解析では全て粗いグリッド上の行列を離散近似で求めているが,実際はガレルキン近似も良く使われている.ガレルキン近似では偏微分方程式を用いず、レストリクション,プロロンゲーション(いずれもグリッド間のべクトルの変換の操作)を用いて粗いグリッド上の行列を作成するため,粗いグリッド上の行列が少し疎でなくなってしまう.例えば2次元の領域を細かいグリッド上で5点差分を用いて離散化していたとしても粗いグリッド上の行列は9点のステンシルとなってしまう.このため並列性のあるスムージング法としては4色オーダリングを用いた4-colorGS法等を用いる必要がある.ガレルキン近似は解析的扱いが困難であるため,数値実験を行ないMG前処理後の固有値分布を解析すると,収束率は離散近似でRB-GS法を用いた場合より少し良く,しかもグリッドレベルを増やしてもその収束率は変わらないことが分かった.

　次に,拡散係数に強い不連続性のあるポアソン方程式に対して解析を行なった.1次元の場合,拡散係数がちょうど区間の中央で変わっている場合は特別な場合で,この時MG前処理後の行列のスペクトル(固有値の集合)は変わらないことを証明した.つまり,この場合,拡散係数が均一の場合と収束率は変わらない.この結果は2次元,3次元に拡張することができ,この特別な問題に対しては拡散係数が一定の場合と収束率は変わらない.それ以外の場合は上の特別な問題で求めた方法と同一の方法では,非常に繁雑になってしまい事実上解析的に求めるのと数値的に求めるのと変わらなくなってしまう.そこで,ある複雑過ぎないモデル問題に対し,MG前処理後の行列の固有値分布の解析を行なった.その結果,前処理後の行列の固有値は,0に非常に近い固有値が1つあり,その固有値と0.7付近の間に2つ,残りは0.7付近と1の間にあった.この例は一例であるが,MG法はこの非常に小さい一つの固有値のために収束率が極端に悪くなってしまうが,MGCG法は極端な話し拡散係数が均一の場合より3反復多く反復すれば収束することが分かる.従って,このような問題に対しては,MG法を単独で用いるより,CG法の前処理として用いることにより理想的な解法となる.

　さらにMGCG法の並列化とその効率的実装についての研究を行なった.MGCG法はMG法とCG法を組み合わせた方法であり,両解法を効率良く並列化する必要がある.CG法は行列ベクトル積,内積,ベクトルの実数倍,和で構成され,MG法はスムージング法、行列ベクトル積,レストリクション,プロロンゲーション,ベクトルの和で構成されている.ベクトルの次元をnとした場合,ベクトルの実数倍,和にはO(n)のデータ並列性があり,内積にはO(n/logn)のデータ並列性がある.使用するプロセッサ数をpとおくと,それぞれの並列演算ステップ数はO(n/p),O(n/p+logp)となり,非常に高い並列性を持っていることが分かる.また,レストリクション,プロロンゲーションは同様にO(n)の並列性を持ち,ベクトルの実数倍と同様に並列演算ステップ数はO(n/p)である.問題は残りの行列ベクトル積とスムージング法である.行列が2次元矩形領域の2階偏微分方程式を通常の5点差分近似で離散化してできた行列である場合,矩形領域をp(＝p_x×p_y)等分し,各小領域のデータをプロセッサに割り当てると,並列演算ステップはO(n/p)となり,必要な通信量はO(√n/min{P_x,P_y})である.ここで,n≫pの場合は通信するデータに比べ,演算数が多くなるため通信と計算のオーバーラップを行なうことにより通信遅延の隠蔽を完全に行なうことができる.スムージング法については,MG法では上の解析でもあるように高並列なスムージング法(減速ヤコビ法,RB-GS等)を用いると先ほどのような問題の場合,収束が極端に悪くなってしまうが,MGCG法では収束の悪化はわずかであるため,高並列なスムージングを行なうことができる.この場合状況は行列ベクトル積とほぼ同様になる,今までの考察では,n≫pの時に非常にうまくいくということであったが,MG前処理を行ないグリッドレベルを増やしていくと(つまりnを減らしていくと)この条件が満たされなくなり,通信オーバーヘッドを隠すことができなくなる.従って,分散メモリ型並列計算機に効率良くMGCG法を実装する為には,以下の問題を解決する必要がある.

　1.最も粗いグリッドを大きくとる.この場台,通信オーバーヘッドは隠せるが,緩和法で近似的に解くとMGCG法の反復回数が増える.

　2.最も粗いグリッドを十分に粗くとる.粗いグリッドでは通信オーバーヘッドは隠せず,またロードバランスが悪くなるが,間題サイズに依存しない反復回数で収束する.

　これらの問題は基本的にMGCG法の収束率と実装するマシンの並列効率のトレードオフの問題と考えることができる.さらに,粗いグリッドで近似的にある程度の精度まで解く場合は,緩和法(または直接法)を用いその精度まで解くのと,さらに粗いグリッドを使いMG法を用いるのとどちらが良いかということにもなる.

　このトレードオフを分散メモリ型並列計算機により評価を行なった.拡散係数が一定の場合は最も粗いグリッドを大きくとっても,そこで近似的にある精度まで解けばMGCG法の収束率はそんなに悪くならない.また,プロセッサ数以上に粗いグリッドを用いその部分は1プロセッサで計算する場合でも,ロードバランスは非常に悪くなるが,プロセッサ数が多過ぎなければその部分はデータは少なく,かつ通信がないため,反復全体に対し占める割合は極僅かである.さらにこの時,問題サイズによらず良い収束率を維持することができることもあり,拡散係数が均一の場合はこの二つの方法には大きな差は見られなかった.しかしながら拡散係数に強い不連続性がある場合は,最も粗いグリッドを大きくとった場合そこでかなりの精度まで解かないとMGCG法の収束率が悪くなってしまうが,プロセッサ数以上に粗いグリッドを用いた場合はその収束率の悪化が前の評価でもあるように押えられるため,この場合はプロセッサ数以上に粗いグリッドを用いても十分な精度で解いた方が収束までの計算時間は短くなる.次に,このMGCG法の性能評価を行なった.その結果,MGCG法はプロセッサ台数に比べほぼスケーラブルであり,他の並列性のある解法に比べ収束するまでの計算時間が格段に短かかった.

　本研究では,拡散係数一定のポアソン方程式、拡散係数に強い非連続性のあるポアソン方程式の解法としてMGCG法の提案を行ない,その収束率の解析,効率的な並列化を行なった.その結果,非常に良い収束率を持つこと,拡散係数に段差がある場合でもほとんど収束までの反復同数は増えず,非常に優れていることが分かった.さらに並列計算機に効率的に実装を行なうことができ,その良い収束率を保ったままプロセッサ台数にほぼスケーラブルな性能を出すことが出来た.MGCG法は良い収束率を持ちロバストで,かつ高い並列性を持つという相反する性質を合わせ持つ,非常に優れた解法である.

　ポアソン方程式,移流拡散方程式等の偏微分方程式は,有限要素法,差分法等により離散化を行ない大規模な疎行列を係数とする連立一次方程式の解法に帰着される.この疎行列の解法にはガウスの消去法等の直接解法とマルチグリッド(MG)法,共役勾配(CG)法等の反復解法があるが,偏微分方程式を離散化してできた行列は比較的条件が良いため,一般には直接法より収束効率の良い反復解法が多く用いられる.本論文では良い収束率をもちかつ高い並列性をもつ反復解法の研究として,反復解法のマルチグリッド法と前処理付き共役勾配法の二つを組み合わせ,CG法の前処理としてMG法を用いるマルチグリッド前処理付き共役勾配(MGCG)法の提案を行ない,その収束率の評価および並列計算機への効率的な実装の研究を行なっている.

　まず本論文では,MGCG法の収束性について解析している.MG法の最も簡単な場合である2グリッド法について,2グリッド法のプレスムージングしか行なわない場合は,スムージング法に減速リチャードソン法の様な前処理行列,反復行列がともに対称な解法を用い,かつ共役勾配法の内積としてある適当な内積を用いることが十分条件であることを証明した.またプレスムージング,ポストスムージングの両方を行なう場合についても条件を与えた.

　次に,このMGCG法の収束率の解析を固有値解析を通して行なっている.MGCG法はCG法の前処理にMG法を用いるものであるため,MG前処理後の行列の固有値分布を求める必要があり,本論文では1,2次元の拡散係数一定のポアソン方程式をモデル問題として解析している.各グリッドにおけるフーリエモード解析より,1次元の場合は定数回反復で厳密解を与えることが示された.また2次元の場合は,固有値分布はほぼ連続的であったため固有値の区間によるMGCG法の収束率の評価が良い評価を与える.MG法と比べた場合,MGCG法の反復回数はほぼMG法の半分となり,MGCG法一反復に必要な演算量はMG法の一反復の1.5倍以下であるため,MGCG法の方が優れている.

　拡散係数に強い不連続性のあるポアソン方程式に対しても解析を行なっている.拡散係数がちょうど区間の中央で変わっている特別な場合については,MG前処理後の行列のスペクトルは変わらず,拡散係数が均一の場合と収束率は変わらないことが示された.その他の場合については,十分意味のあるモデル問題に対し,MG前処理後の行列の固有値分布の解析を行ない,MG法は非常に小さい一つの固有値のために収束率が極端に悪くなるのに対し,MGCG法は拡散係数が均一の場合よりこの例では3反復ほど多く反復すれば収束することがわかり,MGCG法の優越性が示されている.

　さらにMGCG法の並列化とその効率的実装についての研究を行なった.MGCG法はMG法とCG法を組み合わせた方法であり,両解法を効率良く並列化する必要がある.まず,各法の並列化について詳細を検討し,通信遅延の隠蔽などの問題点を解決している.特に,MG前処理を行ないグリッドレベルを増やしていったときの通信オーバヘッドについて,この問題をMGCG法の収束率と実装するマシンの並列効率のトレードオフの問題と捉え,解析・性能評価の結果,MGCG法はプロセッサ台数に比べほぼスケーラブルであり,他の並列性のある解法に比べ収束するまでの計算時間が格段に短かいことが示された.

　以上まとめるに,本論文では拡散係数一定のポアソン方程式,拡散係数に強い非連続性のあるポアソン方程式の解法としてMGCG法の提案を行ない,その収束率の解析,効率的な並列化を行なった.解析の結果,MGCG法は良い収束率をもちロバストで,かつ高い並列性を有する非常に優れた解法であることが示された.なお,本論文におけるMGCG法開発と並列化に関する研究の一部は小柳義夫との共同研究であるが,論文提出者が主体となって研究を行なったもので,論文提出者の寄与が十分であると判断する.

　よって,博士(理学)の学位を授与できると認める.