現在、強い相互作用の基礎理論は量子色力学(QCD)であると考えられている。QCDはクォークとグルーオンを基本的自由度とする非可換ゲージ理論であり、低エネルギー領域では強結合となる。それ故、ハドロンにおける「クォークの閉じ込め」や「カイラル対称性の自発的破れ」などの低エネルギーに特徴的な現象を解析するためには非摂動的な方法が要求される。しかし、現段階では場の理論における非摂動論は確立しておらず、これらの現象に対する我々の理解は不十分である。また、閉じ込めにより、実際に観測される状態はクォークとグルーオンの束縛状態のみであるが、相対論的束縛状態の非摂動的理解も進んでいない。 相対論的束縛状態の非摂動的取り扱いを可能にし、QCDへの応用を期待できるものとして、ハミルトニアン形式における「光円錐量子化法(Light-Front Quantization)」という手法が最近再び注目を集めている。この手法では通常の時間x0ではなく、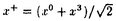 を時間として量子化を行ない、 を時間として量子化を行ない、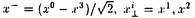 を空間座標として扱う。これらを光円錐座標と呼ぶ。この考え方は約50年前にディラックによって提唱されたものであるが、非摂動的な解析が始まったのはここ数年のことである。光円錐量子化を行なう最大の利点は、摂動的に定義されたFock真空が相互作用を含めてもハミルトニアンの固有状態であるということである(真空の自明性)。これは光円錐座標での分散関係 を空間座標として扱う。これらを光円錐座標と呼ぶ。この考え方は約50年前にディラックによって提唱されたものであるが、非摂動的な解析が始まったのはここ数年のことである。光円錐量子化を行なう最大の利点は、摂動的に定義されたFock真空が相互作用を含めてもハミルトニアンの固有状態であるということである(真空の自明性)。これは光円錐座標での分散関係  より、容易にわかる。すなわち、光円錐座標でのエネルギーp-の非負性より、縦運動量p+もp+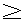 0でなければならない。従って、p+=0モード(以下「ゼロモード」と呼ぶ)を除けば、Fock真空と同じ運動量状態を作ることができないのでFock真空が粒子、反粒子状態と混ざり得ず、相互作用が存在してもハミルトニアンの固有状態になるのである。 0でなければならない。従って、p+=0モード(以下「ゼロモード」と呼ぶ)を除けば、Fock真空と同じ運動量状態を作ることができないのでFock真空が粒子、反粒子状態と混ざり得ず、相互作用が存在してもハミルトニアンの固有状態になるのである。 しかし、そうなると「自発的(あるいは動的な)対称性の破れ」や「 真空」などの「真空の物理」を光円錐量子化で記述することができるのかという問題が生じる。これらの問題に対しては最近ようやく解析が始まり、上の素朴な議論では除いてしまった縦方向の「ゼロモード」が非常に重要な役割を果たすということが徐々に分かってきた。実際、スカラー理論における自発的対称性の破れについては以下のように記述できる。まず、スカラー場 真空」などの「真空の物理」を光円錐量子化で記述することができるのかという問題が生じる。これらの問題に対しては最近ようやく解析が始まり、上の素朴な議論では除いてしまった縦方向の「ゼロモード」が非常に重要な役割を果たすということが徐々に分かってきた。実際、スカラー理論における自発的対称性の破れについては以下のように記述できる。まず、スカラー場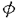 (x)の縦方向ゼロモード (x)の縦方向ゼロモード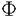 (x⊥)は独立な自由度ではなく「ゼロモード拘束」と呼ばれる拘束を満たす。この拘束を何らかの非摂動的手法で解き、次のようにゼロでない定数部分 (x⊥)は独立な自由度ではなく「ゼロモード拘束」と呼ばれる拘束を満たす。この拘束を何らかの非摂動的手法で解き、次のようにゼロでない定数部分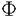 (c)≠0を得ることができたとしよう。 (c)≠0を得ることができたとしよう。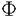 = =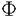 (c)+ (c)+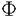 (op).ここで (op).ここで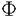 (op)は非ゼロモードによって書かれた演算子部分である。するとそれによって場の真空期待値がゼロでない値を持つ。〈0| (op)は非ゼロモードによって書かれた演算子部分である。するとそれによって場の真空期待値がゼロでない値を持つ。〈0|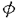 |0〉=〈0| |0〉=〈0|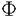 |0〉= |0〉=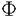 (c)≠0.さらに、このゼロモード拘束の解をハミルトニアンに代入すれば、真空の効果を反映した新しいハミルトニアンを得る。こうして真空が自明のままでも自発的対称性の破れが記述されると考えられる。 (c)≠0.さらに、このゼロモード拘束の解をハミルトニアンに代入すれば、真空の効果を反映した新しいハミルトニアンを得る。こうして真空が自明のままでも自発的対称性の破れが記述されると考えられる。 自発的対称性の破れについては盛んに調べられているが、動的(ダイナミカル)な対称性の破れや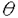 真空についての理解はまだほとんどなされていない。そこで本論文では、このうち「動的な対称性の破れ」を光円錐上で記述することを目指し、次の4体フェルミ理論(4次元のNambu-Jona-Lasinio模型、2次元のGross-Neveu模型)を詳しく調べた。 真空についての理解はまだほとんどなされていない。そこで本論文では、このうち「動的な対称性の破れ」を光円錐上で記述することを目指し、次の4体フェルミ理論(4次元のNambu-Jona-Lasinio模型、2次元のGross-Neveu模型)を詳しく調べた。 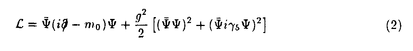 この理論は(m0=0で存在する)カイラル対称性がダイナミカルに破れる模型として最初に導入されたものである。対称性が破れると、フェルミオンが質量(以下ではこれを「物理的質量」と呼ぶ)を獲得する。良くなされるように、本論文でもフェルミオンに内部自由度(U(N)対称性)を与え、非摂動的な手法として1/N展開を使えるようにした。光円錐上では、この模型の満足のいく解析はないが、QCDにおけるカイラル対称性の動的破れを理解するためには避けては通れないものであり、解析をする価値は十分にある。本論文では3種類の解析を試みた。すなわち、(I)補助場を導入し、ゼロモード拘束の考えを利用する方法、(II)フェルミオンのみで行なった解析、(III)和則を使った解析、である。中でも解析(II)を最も詳しく調べ、幾つかの新しい知見が得られた。以下、それぞれを説明する。 (解析I)フェルミ粒子のみの系では、ゼロモード拘束が存在しない。しかし、補助場としてスカラー場を導入し、(2)を書き換えることでゼロモード拘束の考え方を利用できる。まず、フェルミオンを全て積分してしまい、補助場のみの理論を調べた。この場合、正準形式の議論は困難になるが、ゼロモード拘束に相当する方程式を1/N展開すると、その最低次としてギャップ方程式が得られる。(この方法はGross-Neveu模型に対しては前段が行なったが、本論文では4次元のNambu-Jona-Lasinio模型について行なった。)次に、完全には積分をせず、補助場とフェルミオンが共存する系を扱った。実際には便宜のために、補助場に運動項を持たせた系(Yukawa模型)を扱った。この運動項は制御可能なパラメータ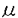 を係数に含み、4体フェルミ理論に を係数に含み、4体フェルミ理論に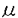 →∞で一致する。この系にディラックの拘束系の量子化を行なうと、スカラー場(補助場)のゼロモードに対する「ゼロモード拘束」を得ることができる。この拘束に1/N展開を用いると、その最低次で方程式 →∞で一致する。この系にディラックの拘束系の量子化を行なうと、スカラー場(補助場)のゼロモードに対する「ゼロモード拘束」を得ることができる。この拘束に1/N展開を用いると、その最低次で方程式 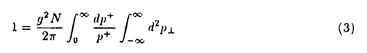 が得られた。これではまだギャップ方程式とは考えられないが、発散する積分の正則化を正しく行なうことでギャップ方程式に帰着することがわかる。解析(II)でも同じものを得るので、このことはそこで説明する。 (解析II)補助場を入れずに解析をする場合には、ゼロモード拘束の考え方は使えない。その代わりに次のように考えられる。光円錐量子化ではフェルミオンの自由度の半分が独立な自由度ではなくなり、ある拘束を満たす。これを「フェルミオン拘束」と呼ぼう。ゲージ理論などではこの拘束は線形なので容易に解けるが、4体フェルミ理論ではその相互作用の非線形性を反映して、拘束も非線形になるため、容易には解けない。これがこの模型の解析を困難にしているのだが、実はここに破れた相の記述の可能性があることがわかる。何故なら、カイラル対称性の有無はフェルミオン拘束を解かなければ議論できず、この拘束を解く際に、対称性の破れた解か、そうでない解かのどちらかを選ぶことになると期待されるからである。 実際に1/N展開の最低次で、フェルミオン拘束から上の方程式(3)が得られる。式(3)には物理的質量が陽に現われておらず、それを決定できないので、このままではギャップ方程式とは考えられない。しかし、この積分の正則化を次のようにすればギャップ方程式になることがわかる。すなわち、この積分には赤外発散と紫外発散の両方存在するが、赤外発散の正則化を紫外発散の切断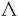 と関係づけて行なうことで物理的質量の情報を入れることができるのである。この特殊な赤外切断の仕方は、光円錐上の理論としてはパリティ不変性を保つ正則化として自然に導入されるということを強調しておきたい。光円錐上でのパリティ変換はp+とp-を入れ換える変換であり、これを保つような正則化はp±< と関係づけて行なうことで物理的質量の情報を入れることができるのである。この特殊な赤外切断の仕方は、光円錐上の理論としてはパリティ不変性を保つ正則化として自然に導入されるということを強調しておきたい。光円錐上でのパリティ変換はp+とp-を入れ換える変換であり、これを保つような正則化はp±<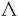 となる。分散関係(1)を考慮すれば、赤外切断が となる。分散関係(1)を考慮すれば、赤外切断が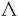 に依存すると共に質量の情報が混入することがわかるだろう。さらにその質量として物理的質量を採用することが、いわゆる自己無撞着性を課すことに相当する。また、この処方は光円錐量子化における根本的な問題を回避する手法として認識することができる。光円錐上の理論では場の2点関数を評価すると粒子の質量の情報が失われ、通常の量子化で得たものと一致しないので、適切な正則化を行なう必要がある。ここで導入したパリティ不変な正則化はその方法の一つと考えられる。 に依存すると共に質量の情報が混入することがわかるだろう。さらにその質量として物理的質量を採用することが、いわゆる自己無撞着性を課すことに相当する。また、この処方は光円錐量子化における根本的な問題を回避する手法として認識することができる。光円錐上の理論では場の2点関数を評価すると粒子の質量の情報が失われ、通常の量子化で得たものと一致しないので、適切な正則化を行なう必要がある。ここで導入したパリティ不変な正則化はその方法の一つと考えられる。 さらにフェルミオン拘束を次のオーダーまで解いた。このオーダーで得られるハミルトニアンの対角化から、フェルミオンと反フェルミオンの束縛状態の方程式が得られる。カイラルGross-Neveu模型において、Nambu-Goldstoneボゾンに相当する状態が存在し、カイラル極限でなくとも、その解析解を求めることに成功した。すなわち波動関数が求まり、カイラル近傍での質量を評価することができた。波動関数を求めることが出来るのは光円錐量子化をハミルトニアン形式で行なう大きな利点である。 (解析III)フェルミオン凝縮の値を光円錐上で計算する方法として、和則を用いたものがある。すなわち1+1次元で言えば 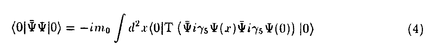 を利用して、右辺の評価より間接的に凝縮の値を求めるのである。特に、N→∞,m0→0では、Nambu-Goldstoneボゾンのカイラル近傍での質量と行列要素のみを用いて右辺を評価することができる。実際に1+1次元のQCDでは尤もな値を与えている。しかし実は、式(4)は通常の光円錐量子化では導出できないものである。従って、少なくとも他の手法と和則の計算が同じ値を与えるかを調べる必要があろう。我々は解析(II)によってNambu-Goldstoneボゾンに対する情報を得ることが出来たので、それを用いて和則の計算が解析(II)の凝縮の値を再現するかを試みた。その結果、正しく再現することがわかった。これは光円錐上における和則に対するはじめてのチェックである。 以上のように3つの方法によって動的対称性の破れが光円錐量子化法で如何にして記述されるかを調べた。光円錐量子化法の内包する原理的な問題をうまく回避することで対称性の破れた相を記述することができ、破れた相でも相対論的束縛状態を記述するのに非常に便利な枠組であることが認識された。 |