1987年の銅酸化物高温超伝導体の発見以来、1次元強相関電子系は活発に研究されている。1次元強相関電子系の中には、ハバード模型、超対称t-J模型、バリエフ模型等、厳密に解ける模型がある。これらの模型の性質は従来、座標ベーテ仮説法により詳しく調べられてきた。一方、量子逆散乱法による取り扱いは、超対称t-J模型を除いて、研究が進んでいない。本論文では、主に1次元ハバード模型に焦点を当て、周期的境界条件 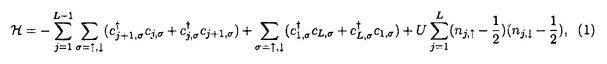 及び、開いた境界条件(開放端境界条件) 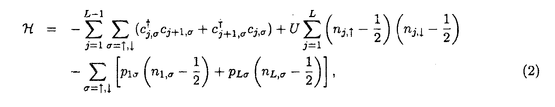 のそれぞれの場合について、量子逆散乱法の枠組みに基づいて可積分性を議論した。 周期的境界条件の1次元ハバード模型(1)はリープ-ウーによって座標ベーテ仮説法により解かれた。ベーテ方程式と呼ばれる運動量を決定する方程式を解析することにより、基底エネルギー、素励起、磁化率、比熱などの物理量が評価された。特に、有限サイズ補正法により、ヴォイナロヴィッチは基底状態付近の低エネルギースペクトルを決定した。この結果、1次元ハバード模型の低エネルギー状態は朝永-ラッティンジャー液体理論で記述されることが示された。 開いた境界条件の1次元ハバード模型(2)は境界外場がない場合にシュルツによって解かれた。浅川-鈴木は、より一般的な枠組みで座標ベーテ仮説法を適用し、境界に化学ポテンシャルを付加した場合(p1↑=p1↓=pL↑=pL↓=p)を解いた。また、彼らは有限サイズ補正法を用いて、模型の低エネルギー状態がカイラル朝永-ラッティンジャー液体理論で記述されることを示した。我々は、ベーテ仮説波動関数の無矛盾性条件を考察することにより、可解な開いた境界外場を分類した。この結果、ベーテ仮説法で解ける可解な境界外場は(a)化学ポテンシャル、(b)磁場の2通りであることを明らかになった。右端の境界条件と左端の境界条件は独立ゆえ、可解な開いた境界条件は次の4通りである。 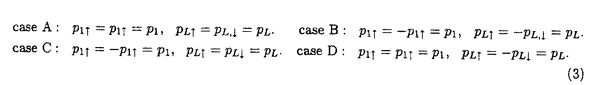 我々は、それぞれの場合に対応するベーテ方程式を導出した。いずれの場合も低エネルギー状態はカイラル朝永-ラッティンジャー液体理論で記述される。 一般に座標ベーテ仮説法によって厳密に解くことができる1次元量子系の模型には可解な2次元古典統計系が対応する。可解な2次元古典統計系はスペクトラルパラメーターを含む交換する転送行列の族を持つ。転送行列をスペクトラルパラメーターで対数微分することによって、ハミルトニアンを含む1次元量子系の無限個の包含的な保存量が得られ、それによって、模型の完全可積分性が示される。 転送行列の交換性はそれを構成するL-演算子がヤン-バクスター関係式 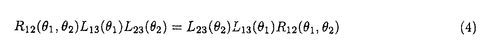 を満たすことによって証明される。ここで、R12(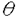 1, 1,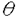 2)はR-行列と呼ばれる要素がc-数の行列である。従来知られている多くの模型ではR-行列はスペクトラルパラメーターに関して差法性 2)はR-行列と呼ばれる要素がc-数の行列である。従来知られている多くの模型ではR-行列はスペクトラルパラメーターに関して差法性  を持ち、ヤン-バクスター方程式 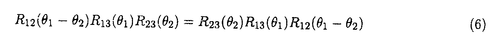 を満たす。 1986年、シャストリーはジョルダン-ウィグナー変換を用いて、1次元ハバード模型を同値なスピン模型に変換し、対応する2次元可解格子模型を構成した。それは、2枚の対称6頂点フリーフェルミオン模型が層間でイジング型の相互作用をする模型である。この模型のL-演算子は2個の対称6頂点フリーフェルミオン模型のL-演算子のテンソル積にdecoration演算子をかけたものになっている。シャストリーは対称フリーフェルミオン模型のL-演算子の満たすdecoratedスター・トライアングル関係式を用いて、1次元ハバード模型に同値なスピン模型のヤン-バクスター関係式(4)を証明した。得られたR-行列はスペクトラルパラメーターに関する差法性(5)を持たないという著しい特徴を持つ。対称フリーフェルミオン模型は非対称フリーフェルミオン模型の特別な場合である。ここで、非対称フリーフェルミオン模型とは8頂点模型のボルツマン重率の間に対称性を課さず、いわゆるフリーフェルミオン条件のみを仮定した最も一般的なフリーフェルミオン模型である。非対称フリーフェルミオン模型のL-演算子は通常のスペクトラルパラメーター以外にカラー変数と呼ばれるパラメーターを持ち、2パラメーターのヤン-バクスター方程式を満たす。我々は、カラー変数を用いて、decoratedスター・トライアングル関係式を非対称フリーフェルミオン模型の場合に拡張した。この結果、decoratedスター・トライアングル関係式はフリーフェルミオン模型に特有な隠れた代数構造であることを明らかになった。 1次元ハバード模型に対するシャストリーのR-行列はスペクトラルパラメーターに関する差法性(5)を持たないが、次の形のヤン-バクスター方程式を満たすと予想されてきた。 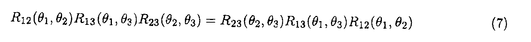 本論文において、我々はコレパノフによるtetrahedralザモロチコフ代数を利用してこの予想を証明した。tetrahedralザモロチコフ代数はヤン-バクスター方程式とtetrahedron方程式の中間の代数構造であり、その解からtetrahedron方程式の解が系統的に構成できると考えられている。コレパノフは対称8頂点フリーフェルミオン模型に関連するtetrahedralザモロチコフ代数の解を与えた。我々は、コレパノフの解が対称8頂点フリーフェルミオン模型のスター・トライアングル関係式とdecoratedスター・トライアングル関係式の拡張になっていることを見出した。さらに、6頂点極限において3個の演算子の積の作る線形空間が8次元から6次元に縮退することを具体的に示した。これらの結果を利用してシャストリーのR-行列がヤン-バクスター方程式(6)を満たすことを初めて証明した。また、R-行列とL-演算子の間の関係を用いて、R-行列のヤン-バクスター方程式(7)からヤン-バクスター関係式(4)を導くことができる。一方、我々は、ヤン-バクスター関係式からラックス方程式が導けることも示した。すなわち、R-行列のヤン-バクスター方程式(7)は1次元ハバード模型の可積分性の研究において最も重要かつ基本的な関係式である。また、このR-行列は初期条件、ユニタリー性、交差対称性等の性質を持つことも示した。さらに、R-行列を用いて可解な2次元2層格子模型を構成し、対応する可積分1次元ハミルトニアンを導出した。 1987年、オルメディジャ-和達-阿久津によりフェルミオン変数を成分に持つ1次元ハバード模型のL-行列が提出され、対応するフェルミオン的R-行列が求められた。フェルミオン的R-行列はシャストリーのR-行列から対角行列でツイストして得られる。我々はこのフェルミオン的R-行列の性質を調べ、次数付き(graded)ヤン-バクスター方程式、ユニタリー性、交差対称性等の性質を持つことを示した。フェルミン的R-行列の次数付きヤン-バクスター方程式はシャストリーのR-行列のヤン-バクスター方程式(7)と同値である。また、フェルミオン的R-行列はハミルトニアン(1)のSO(4)対称性に対応する対称性を持つことを発見した。ハミルトニアン(1)は部分的粒子-空孔変換 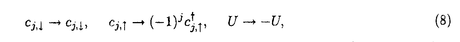 のもとで不変であるが、この変換に対応するR-行列の変換性も明らかにした。一方、フェルミオン的な高次の保存量がハミルトニアン(1)と同様に有限格子でSO(4)対称性、無限格子でヤンギアン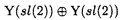 対称性を持つことを確認した。 対称性を持つことを確認した。 開いた境界条件の場合(2)の可積分性はゾウによって最初に議論された。彼は(2)をジョルダンウィグナー変換によって同値なスピン模型に変換し、シャストリーのR-行列を用いて可積分性を議論した。本論文ではフェルミオン的R-行列を用いて、(次数付き)反射方程式 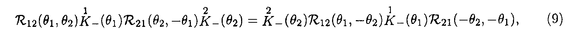 を定式化した。我々は、反射方程式(9)の対角解K-(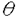 )には2種類あり、それぞれ(a)境界化学ポテンシャル、(b)境界磁場に対応することを示した。この結果は座標ベーテ仮説法での可解性と一致する。我々は、反射方程式の解を用いて交換する転送行列を構成し、これによって開いた境界条件の場合の1次元ハバード模型(2)の可積分性を証明した。また、反射方程式(9)の2種類の対角解がフェルミオン的R-行列の部分的粒子-空孔変換によって結びついていることを示した。 )には2種類あり、それぞれ(a)境界化学ポテンシャル、(b)境界磁場に対応することを示した。この結果は座標ベーテ仮説法での可解性と一致する。我々は、反射方程式の解を用いて交換する転送行列を構成し、これによって開いた境界条件の場合の1次元ハバード模型(2)の可積分性を証明した。また、反射方程式(9)の2種類の対角解がフェルミオン的R-行列の部分的粒子-空孔変換によって結びついていることを示した。 1次元強相関電子系の他の模型としてバリエフ模型 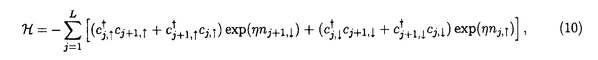 がある。この模型は1990年にバリエフによって座標ベーテ仮説法によって解かれた。我々は、ハバード模型の場合の方法論を適用して1次元バリエフ模型の可積分性の証明をした。実際、高次の保存量、L-演算子およびヤン-バクスター関係式を満たすR-行列を具体的に求めた。得られたR-行列はスペクトラルパラメーターに関して差法性(5)を持たない等、ハバード模型のR-行列と極めてよく似た性質を持つことが明らかになった。 以上、本論文は、厳密に解ける1次元強相関電子系の可積分性を量子逆散乱法の枠組みに基づいて議論した。我々の結果は、1次元強相関電子系の可積分性に関して新しい知見を与え、代数的ベーテ仮説法等、更なる発展の基礎となるものである。 |