近年、リーに基づく力学系のハミルトン系としての定式化およびそれに基づく解析法が発展してきており、剛体、弾性体、プラズマ、量子論等、多くの物理系に表れる方程式が調べられている。流体力学に関しては、アーノルドにより、非圧縮完全流体の支配方程式(オイラー方程式)が定式化されており、リー群としては体積を保存する微分同相写像群が用いられている。 アーノルドはさらに、この群に自然なリーマン計量を導入してオイラー方程式を測地線方程式としても定式化し、断面曲率の計算から不安定性の解析を行った。ここでの不安定性解析とは、リーマン多様体上の測地線に変分ベクトル場(ヤコビ場)による摂動をあたえたとき、摂動を受けた測地線が非摂動測地線に再び近づくのかそれとも離れてゆくのかを、リーマン計量から決まる距離に関して調べることである。したがって、系の定式化の際に導入するリー群とリーマン計量の物理的な意味が重要になる。 本論文ではこの解析法を、完全流体中の孤立した細い糸状の渦(渦糸)の運動を記述する局所誘導方程式(LIE)に適用する。そして渦糸の接ベクトルが局所的な剛体回転運動をおこなっていることに着目し、リーマン幾何の立場から渦糸の運動の不安定性を調べる。後に示すように、この論文で導入する計量は渦糸の形の変化を調べるのに適当なものになっていろ。 本論文ではLIEの解析の準備として、LIEの歴史的背景と導出方法、リー群に基づくハミルトン系の構成法、およびそれに基づくリーマン幾何学的定式化の基礎を簡潔に紹介する。 続いてこれらの基礎に基づき、LIE解析のベースとなってる自由な剛体の運動の定式化及びその解析を行う。自由な剛体の運動の支配方程式は、  である。ここで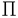 は剛体の物体座標での角運動量、 は剛体の物体座標での角運動量、 は剛体の物体座標での角速度であり、両者は慣性テンソルIによって、 は剛体の物体座標での角速度であり、両者は慣性テンソルIによって、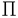 =I =I という関係により結びつけられている。方程式(1)のハミルトン系としての定式化は古くから知られ、使われるリー群はSO(3)(3次元ユークリッド空間の回転群)である。しかしリーマン幾何に基づく測地線方程式としての定式化、およびヤコビ場による解析はなされておらず、また、後に続くLIEの定式化へのイントロダクションとしても適当であるため、この解析を行った。式(1)による剛体の自由な回転では、3つの主軸のうち、最長及び最短の軸のまわりの回転が安定である一方、残りの軸に関する回転は不安定であることが知られている。ヤコビ場の支配方程式の直接の解析により同様の安定性が示される一方、断面曲率の計算ではその符号はほぼ上記の結果を再現するが、安定軸に対してはわずかに負となりうる方向があることが示された。この結果は、断面曲率の符号は安定性を示唆するがそれだけでは不十分であり、ヤコビ場の情報が必要であることを示している。 という関係により結びつけられている。方程式(1)のハミルトン系としての定式化は古くから知られ、使われるリー群はSO(3)(3次元ユークリッド空間の回転群)である。しかしリーマン幾何に基づく測地線方程式としての定式化、およびヤコビ場による解析はなされておらず、また、後に続くLIEの定式化へのイントロダクションとしても適当であるため、この解析を行った。式(1)による剛体の自由な回転では、3つの主軸のうち、最長及び最短の軸のまわりの回転が安定である一方、残りの軸に関する回転は不安定であることが知られている。ヤコビ場の支配方程式の直接の解析により同様の安定性が示される一方、断面曲率の計算ではその符号はほぼ上記の結果を再現するが、安定軸に対してはわずかに負となりうる方向があることが示された。この結果は、断面曲率の符号は安定性を示唆するがそれだけでは不十分であり、ヤコビ場の情報が必要であることを示している。 次に、渦糸の局所誘導方程式(LIE)、 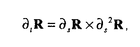 の解析を行う。ここで、tは時間、sは渦糸の弧長、R(t,s)は渦糸の位置ベクトルをあらわし、∂xは変数Xに関する偏微分である。この方程式の両辺をさらにsで偏微分すると,物理空間における渦糸の接ベクトルt(t,s)=∂sR(t,s)の支配方程式が導かれる。すなわち、  である。式(1)と式(2)を比べると、tが剛体の角運動量運動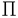 に、∂s2tが剛体の角速度 に、∂s2tが剛体の角速度 に対応していることが分かる。この対応に基づき、G=C∞(L,SO(3))という無限次元リー群を導入する。ここで、Lは弧長sの空間を表し、 C∞(A,B)は空間Aから空間Bへの無限階微分可能な写像の全体をあらわす。言い換えれば群Gは、渦糸の各点に回転群SO(3)の元を対応させたものである。ハミルトニアン、 に対応していることが分かる。この対応に基づき、G=C∞(L,SO(3))という無限次元リー群を導入する。ここで、Lは弧長sの空間を表し、 C∞(A,B)は空間Aから空間Bへの無限階微分可能な写像の全体をあらわす。言い換えれば群Gは、渦糸の各点に回転群SO(3)の元を対応させたものである。ハミルトニアン、 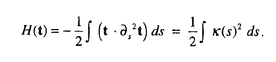 (ここで、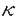 (s)は物理空間での渦糸の点sにおける曲率)を導入し、標準的手法によってリー括弧からポアソン括弧を構築することにより、ハミルトン方程式dF/dt={F,H}が式(2)に一致することが示される。さて、このハミルトニアンからリーマン計量が自然が自然に決められるが、リー群G=C∞(L,SO(3))の接ベクトルu,vに対し、内積は, (s)は物理空間での渦糸の点sにおける曲率)を導入し、標準的手法によってリー括弧からポアソン括弧を構築することにより、ハミルトン方程式dF/dt={F,H}が式(2)に一致することが示される。さて、このハミルトニアンからリーマン計量が自然が自然に決められるが、リー群G=C∞(L,SO(3))の接ベクトルu,vに対し、内積は,  である。ここで、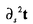 は変数sに関するf(s)の不定積分(積分定数はゼロとおく)である。式(3)からリーマン接続による共変微分が求められ、測地線方程式▽uu=0が は変数sに関するf(s)の不定積分(積分定数はゼロとおく)である。式(3)からリーマン接続による共変微分が求められ、測地線方程式▽uu=0が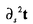 の支配方程式になることが示される。したがって の支配方程式になることが示される。したがって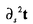 がリー代数の元に対応し、そのノルムは∫ がリー代数の元に対応し、そのノルムは∫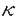 (s)2ds、すなわち渦糸の曲率 (s)2ds、すなわち渦糸の曲率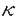 (s)の二乗を、渦糸全体に渡って積分したものとなる。したがってこの計量による不安定性解析は、渦糸の形の変化を調べるのに適当なものであるといえる。 (s)の二乗を、渦糸全体に渡って積分したものとなる。したがってこの計量による不安定性解析は、渦糸の形の変化を調べるのに適当なものであるといえる。 測地線の不安定性解析の前に、この定式化の表現論について言及する。リー代数の表現を変えることにより、任意の整数nに対して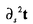 の支配方程式をハミルトン方程式として、 の支配方程式をハミルトン方程式として、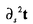 の支配方程式を測地線方程式として得ることができることを示す。特にn=2の場合には、式(2)を直接測地線方程式として得ることができる。また、曲率等のスカラー量は表現によらない。 の支配方程式を測地線方程式として得ることができることを示す。特にn=2の場合には、式(2)を直接測地線方程式として得ることができる。また、曲率等のスカラー量は表現によらない。 最後に、渦糸の安定性に関連する断面曲率の計算を行う。渦輪や螺旋渦の解析の結果、曲率の符号が通常の線形安定性による結果と同様の傾向をもつことが示される。すなわち、渦糸の持つ典型的な波長より短い波長の摂動に対しては断面曲率は正になり、長い波長をもつ摂動に対しては負になるのである。この結果は我々の定式化の妥当性を示すものであるといえる。また、螺旋渦に関しては、測地線の大域的性質と深い関連がある共役点の存在を示す。共役点の存在、および曲率が正になる方向が多い、という2つの事実は、非線形性安定性を示唆するが故に重要であり、今後の応用が期待される。 |