学位論文要旨
| No | 112409 | |
| 著者(漢字) | 前橋,英明 | |
| 著者(英字) | ||
| 著者(カナ) | マエバシ,ヒデアキ | |
| 標題(和) | 相互作用するフェルミ粒子系の電気伝導度 | |
| 標題(洋) | Electrical Conductivity in Interacting Fermions | |
| 報告番号 | 112409 | |
| 報告番号 | 甲12409 | |
| 学位授与日 | 1997.03.28 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(理学) | |
| 学位記番号 | 博理第3189号 | |
| 研究科 | 理学系研究科 | |
| 専攻 | 物理学専攻 | |
| 論文審査委員 | ||
| 内容要旨 | 電子間相互作用による電気伝導度, 一方、電流が保存するとき抵抗は生じない、という正しい結果を再現する他の定式化として、森公式に基づく記憶関数による方法がある。この方法は、電流を保存しない散乱過程の最低次で種々の系の抵抗を実際に評価できるという利点を持っている。ところが、結晶中では連続空間の場合と異なり電流は電子の運動量でなく群速度によって決定されるため、運動量が保存されるnormal散乱であっても一般には電流は保存されない。しかしながら、例え電流が保存されないような場合でも運動量を散逸する機構がなければ抵抗は生じないと期待される。このとき、記憶関数による方法では、電流保存の破れは考慮されているが運動量保存の効果が考慮されていないので、一般に零でない誤った抵抗を与えてしまう。これは高周波数展開による近似であることに起因している。 本研究の大きな目的は、不純物もUmklapp過程もない場合に零抵抗を与える正しい定式化の下で、不純物あるいはUmklapp過程がある場合の結晶格子中での電気抵抗を考察することである。従って、山田、芳田と同じく、Fermi流体論に基づくEliashbergによる久保公式の定式化から出発する。まず、不純物のない連続体の場合に運動量保存に関するWard-高橋恒等式を用いて抵抗のT2-項が生じないことに加えて、Drude weightも電子間相互作用によって繰り込まれないことを示した。これは を考えた。この系の ここで、 以下、 不純物がある場合、不純物散乱の輸送緩和時間が、最も短い電子-電子散乱の輸送緩和時間よりも十分短ければ によって与えられる。ここで 上の結果は、たとえ電子-電子散乱を通しては運動量を散逸する機構がなくても不純物があれば一般には有限のT2-項が生じることを示す。これはMatthiessenの規則の破れの特殊な場合と理解することができる。従って、不純物がなくてもUmklapp過程があれば、normal過程も抵抗に寄与し得ることも示唆される。この立場から不純物がない場合のd次元(d 無限次元系の抵抗は準粒子の減衰定数, を持つd次元電子系において、Umklapp散乱が存在する条件はchemical potential, 次にd=2の場合を考察する。2次元電子系では 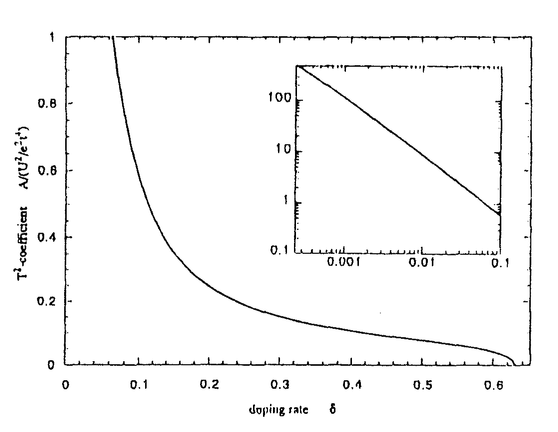 | |
| 審査要旨 | 電気伝導度は固体物理学の分野において、非常に基本的な物理量であり、実験との比較においても重要な役割を果たす。しかし実際に微視的なモデルから出発して理論的に計算しようとする場合には様々な困難があり、固体物理学の中でも難しい問題の一つになっている。本研究は、この問題に真正面から取り組み、低温でかつ弱い不純物散乱という限られた領域ではあるが、電気伝導度および電気抵抗に関する信頼できる計算を展開した。系が並進対称性を持つ場合、一旦動き出した系には緩和機構が働かないので、電気抵抗はゼロになるはずである。まず、本研究では、このことが常に成立するような計算手法を開発し、次に不純物散乱、および電子間相互作用による散乱を考慮した。その結果、フェルミ面の形状によっては、今まで考えられなかったような新しい電気抵抗の温度依存性が生じうることを見出した。 金属の電気抵抗は低温で格子との散乱が無視できる場合には
の形に書けると考えられている。ここで第1項のR0は不純物による抵抗であり、第2項の温度Tの2乗に比例する項は、電子間相互作用によるUmklapp散乱によって生じると理解されている。このことは半現象論的にボルツマン方程式を用いて得られるが、微視的理論によって計算するのは容易ではない。線形応答理論を用いれば、電気伝導度は電流-電流応答関数を計算することによって得られる(久保公式)。不純物散乱だけがある場合には、どのようなファインマン・ダイヤグラムを足し合わせれば抵抗R0が得られるかはわかっている。一方、電子間相互作用によるT2に比例する抵抗については、つい最近山田-芳田によって定式化され、結晶格子のない連続空間ではUmklapp散乱がないために電子間相互作用による抵抗は現れないことが示されたばかりである。 本論文では、この山田-芳田の理論を、結晶格子がありフェルミ面が任意の形である場合に拡張することに成功した。本論文の第一章は序、第二章ではフェルミ流体論に基づく久保公式の定式化を紹介している。第三章では電気伝導度に対する一般的な定式化を行った。不純物散乱の強さに関しての2次摂動、および温度に対してT2まで(電子間相互作用に関して2次まで)の範囲で電気抵抗を計算した。得られた定式化は、従来の記憶関数による方法の一般化となっており、任意の形のフェルミ面の場合に適用できるようになっている。従来の記憶関数の方法では、系が並進対称性を持っていても、フェルミ面の形によっては電気抵抗を与えてしまうという欠陥があったが、本論文で得られた定式化では正しい結果を出すことが示された。 さらにこの定式化に基づいて、第四章では電気抵抗の温度依存性を具体的に求め、今まで予想されていなかった結果を得た。すなわち、電子間相互作用によるnormal散乱はそれだけでは抵抗に寄与しないが、不純物散乱が存在するとT2に比例する抵抗を与えるということである。これは抵抗が各散乱過程の寄与の和であるというMatthiessenの規則が成立しないということを示している。さらにこの場合、抵抗は高温で頭打ちになり、R0より大きなある一定値に近付くということが示された。このような温度依存性は、強相関電子系の実験で測定される可能性があると考えられる。 また不純物散乱の代わりにUmklapp散乱がある場合にも、normal散乱がT2の寄与を与えることが示された。具体的には、第五章で無限次元系の場合、第六章で2次元系の場合が調べられている。なお、2次元の変曲点を持たない閉じたフェルミ面の場合は特殊であり、normal散乱は抵抗に寄与せずUmklapp散乱のみがT2の抵抗を与えることが示された。2次元ハバードモデルはこの場合に相当する。この時の具体的な計算によるとhalf-fillingに近付くとT2の係数が発散するということも示された。最後の第七章は結論に当てられている。 このように本論文では、微視的なモデルに基づいた信頼できる定式化によって、電気抵抗が系統的に調べられることを示し、場合によっては今まで知られていなかったような電気抵抗の温度依存性が可能であることを示した。これらの点で、本研究は大いに価値があると考えられる。本論文の内容は、英文雑誌に投稿予定である。よって審査員一同は、本論文が博士(理学)の学位を授与するにふさわしいものであると認定した。 | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/53949 |
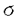 (
(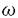 ,T),(
,T),(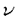 ,短距離クーロン相互作用,U,を持つ結晶格子中の電子系
,短距離クーロン相互作用,U,を持つ結晶格子中の電子系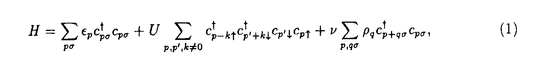
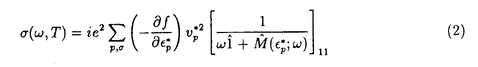
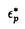 は準粒子の励起エネルギー、
は準粒子の励起エネルギー、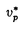 は準粒子の群速度であり、
は準粒子の群速度であり、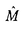 (
(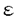 ;
;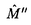 (
(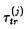 ,を持つことが分かる。不純物もUmklapp散乱もない場合は、
,を持つことが分かる。不純物もUmklapp散乱もない場合は、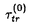 =∞)を持つ。これが、運動量を散逸する機構がなければ抵抗は生じないことの数学的表現である。一方、従来の高周波数展開による記憶関数の虚部はUについて最低次までで
=∞)を持つ。これが、運動量を散逸する機構がなければ抵抗は生じないことの数学的表現である。一方、従来の高周波数展開による記憶関数の虚部はUについて最低次までで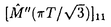 と一致し、群速度が保存しないので一般に有限である。従来の記憶関数による方法では,この行列としての性質が欠如していたため、Uについて最低次でさえ一般には正しくなかったと理解することができる。
と一致し、群速度が保存しないので一般に有限である。従来の記憶関数による方法では,この行列としての性質が欠如していたため、Uについて最低次でさえ一般には正しくなかったと理解することができる。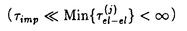 、抵抗は(2)式より
、抵抗は(2)式より
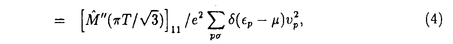
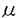 はchemical potentialである。すなわち、この場合は従来の記憶関数による方法で正しい。Min
はchemical potentialである。すなわち、この場合は従来の記憶関数による方法で正しい。Min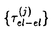 は1/T2に比例するので、十分低温では抵抗はR0+AT2で与えられ、電流が保存しなければAは有限である。従ってUmklapp散乱がない場合でもnormal散乱だけで抵抗のT2-項が生じるという結果が得られた。しかしながらこの場合は、電子-電子散乱が常に運動量を保存することを反映して、温度が高くなると抵抗は頭打ちになり、ある値
は1/T2に比例するので、十分低温では抵抗はR0+AT2で与えられ、電流が保存しなければAは有限である。従ってUmklapp散乱がない場合でもnormal散乱だけで抵抗のT2-項が生じるという結果が得られた。しかしながらこの場合は、電子-電子散乱が常に運動量を保存することを反映して、温度が高くなると抵抗は頭打ちになり、ある値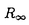 =(1+
=(1+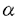 )R0に近づいていくことが分かった。実際、次のような分散を持つ低電子数密度の3次元系についてAと
)R0に近づいていくことが分かった。実際、次のような分散を持つ低電子数密度の3次元系についてAと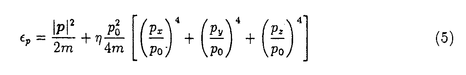
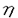 はFermi面のわずかな球面からのずれを表し、poはFermi運動量のスケールである。このとき、Aと
はFermi面のわずかな球面からのずれを表し、poはFermi運動量のスケールである。このとき、Aと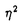 に比例し有限であった。しかし、2次元の変曲点を持たない閉じたFermi面の場合は特殊でA=
に比例し有限であった。しかし、2次元の変曲点を持たない閉じたFermi面の場合は特殊でA=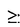 2)、特に高次元と2次元電子系の抵抗を考察した。
2)、特に高次元と2次元電子系の抵抗を考察した。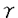 ,のみによって決まることが知られている。このとき、全ての電子数領域で抵抗のT2-項は零でない。また、一般に
,のみによって決まることが知られている。このとき、全ての電子数領域で抵抗のT2-項は零でない。また、一般に
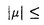 2t(d-1)を満たすことである。d→∞では2dt2=t*2(t*〜O(1))とスケールされるので有限の
2t(d-1)を満たすことである。d→∞では2dt2=t*2(t*〜O(1))とスケールされるので有限の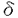 ,依存性を記憶関数の方法によって実際に求めた。結果を下図に示す。特にhalf-fillingでFermi面がネストして1次元的になることを反映して、
,依存性を記憶関数の方法によって実際に求めた。結果を下図に示す。特にhalf-fillingでFermi面がネストして1次元的になることを反映して、