1次元ハイゼンベルグ模型は可積分な磁性の模型として広く研究されており、その基底状態や励起状態はベーテ仮説法によって与えられる。しかし、その有限温度における物理的諸量に対しては、解析的な計算は依然として困難である。有限温度における分配関数を求める為には、無限個の状態についてのエネルギーを与えなくてはいけないためである。このような方法としてはストリング仮説をもちいた計算法があげられる。ストリング仮説によって励起状態のベーテ仮説解を予測し足しあげるのである。 これに対して近年発展してきた手法に、1次元量子系であるハイゼンベルグ模型を2次元古典系に対応させて、種々の物理量を計算するものがある。バクスター公式によると、1次元S=1/2ハイゼンベルグ模型は2次元可解格子模型であるバーテックス模型に対応させることができる。可解な模型である事から、バーテックス模型もまた、ベーテ仮説法によって解析できる。また、バーテックス模型は交差対称性やZ不変性など解析に役立つさまざまな対称性も持っている利点がある。 バクスター公式を有限温度に拡張することによって、1次元量子系の分配関数を、格子模型の転送行列で表すことができる。この拡張を「有限温度バクスター公式」と呼ぶ。1次元量子系におけるサイトの数をNとし、2次元正方格子の大きさをN×Mとする。Mが無限大になる極限において、2つの系が同一視される。 ここで、この極限には注意が必要である。可解格子模型の特徴的なパラメータであるスペクトルパラメーターuに量子系の温度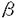 =1/kBTがu= =1/kBTがu=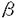 /Mとして含まれているからである。この段階でM→∞の極限をとると、有限温度の情報が格子模型においていっさい含まれないばかりか、その転送行列が単位行列となり、全ての固有値が縮重してしまう。ここで、有益なトリックとして、交差対称性をもちいて格子を90度回転させ、さらにN→∞の熱力学的極限をM→∞の極限よりも先に実行する操作がある。これにより、有限温度における量子系の物理量の解析が回転後の格子における長さMの転送行列の縮重しない固有値より与えられる。特に自由エネルギーは最大固有値のみによって表されることになる。注意するべきことは、最大固有値の計算にあたってはMを有限のパラメータとして扱う有限サイズ補正を考慮し、最後にM→∞の極限を求めるということである。このようにして、量子系においては多数の励起状態に関係した分配関数の低温展開が、古典系においては最大固有値のみの有限サイズ補正によって与えられる。 /Mとして含まれているからである。この段階でM→∞の極限をとると、有限温度の情報が格子模型においていっさい含まれないばかりか、その転送行列が単位行列となり、全ての固有値が縮重してしまう。ここで、有益なトリックとして、交差対称性をもちいて格子を90度回転させ、さらにN→∞の熱力学的極限をM→∞の極限よりも先に実行する操作がある。これにより、有限温度における量子系の物理量の解析が回転後の格子における長さMの転送行列の縮重しない固有値より与えられる。特に自由エネルギーは最大固有値のみによって表されることになる。注意するべきことは、最大固有値の計算にあたってはMを有限のパラメータとして扱う有限サイズ補正を考慮し、最後にM→∞の極限を求めるということである。このようにして、量子系においては多数の励起状態に関係した分配関数の低温展開が、古典系においては最大固有値のみの有限サイズ補正によって与えられる。 また、スピン相関長についても同様に格子模型における対応を与えることができる。我々は量子系のスピン演算子に対応したバーテックスに対する統計重率を古典系で新たに定義することにより、相関長の温度依存性を格子模型の転送行列の最大および3番目の固有値の有限サイズ補正の比によって与えた。 ここからは転送行列の固有値の有限サイズ補正を求める事が主題となる。固有値はベーテ仮説方程式のM個の解によって与えられる。M→∞の極限においては、ベーテ仮説方程式も固有値の表式も積分で書き表され計算できる。一方、有限サイズでは多数の解による和を含む式を解析しなければいけない。そのために、広く使われているオイラー・マクロウリン公式を用いる。ベーテ仮説方程式の解密度を定義し、オイラー・マクロウリン公式による展開の最初の数項を適用する。これによって積分として評価した場合からの補正が、積分の両端の解とその近辺の解密度を含むウィーナー・ホップ型の積分方程式によって与えられる。この積分方程式は、フーリエ変換したのち現れる関数を上半面正則なものと下半面正則なものに分割し、主要な留数を用いて近似計算することにより解くことができる。解分布の両端に対応する補正として、積分核が共通である積分方程式を2度解くことにより、XXXハイゼンベルグ模型について対数補正まで含めた低温展開の最初の2項が解析的計算によって与えられた。 ここで用いられたさまざまな近似に注目したい。 まず、オイラー・マクロウリン公式である。本来等間隔の和を積分で近似するため用いられるこの公式をベーテ仮説法に適用するため、ベーテ仮説解の解密度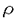 (x)を用いた。分布の境界に存在する解を (x)を用いた。分布の境界に存在する解を としたとき、(M としたとき、(M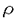 ( ( ))-nの形のM依存性をもつ高次微分項を無視することにより積分方程式を得た。ところが、積分方程式の結果より ))-nの形のM依存性をもつ高次微分項を無視することにより積分方程式を得た。ところが、積分方程式の結果より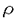 ( ( )が1/M程度の大きさであることが分かった。このため、いままで一般に用いられてきた、このオイラー・マクロウリン公式による展開において高次微分項がMのオーダーとして無視しうるという解釈が困難になった。 )が1/M程度の大きさであることが分かった。このため、いままで一般に用いられてきた、このオイラー・マクロウリン公式による展開において高次微分項がMのオーダーとして無視しうるという解釈が困難になった。 そこで、高次微分項の影響を評価するため、まずXX模型に対して自由エネルギーの計算を行った。XX模型はフリーフェルミオン模型と等価であり、厳密解が知られている。これとの比較によって、オイラー・マクロウリン展開を用いた計算の評価をすることができる。この模型ではベーテ仮説方程式は自明なものとなり、解密度も厳密に与えられる。固有値の表式に対してオイラー・マクロウリン公式を高次微分項まで含めて慎重に適用した。結果としては、自由エネルギーの低温展開が正しく与えられた。さらにその過程において、オイラー・マクロウリン公式による展開の高次微分項は、固有値を求める際には、その固有値を与える積分の核となる関数の特異点の構造に伴い、低温展開としての高次項にのみ影響を及ぼしうることが分かった。すなわち、オイラー・マクロウリン展開が自然に低温展開となることを示すことができた。このXX模型について行なった解析はウィーナー・ホップ型積分方程式を解く場合に用いたのとほとんど同じ一般的な関数について行ったから、他の模型への拡張は素直にできる。 そこで、次にXXZ模型についても同様の考察をおこなった。XXZ模型についても解密度関数などはベーテ仮説方程式から与えられるウィーナー・ホップ型積分方程式を解くことで求まり、固有値もXX模型と類似の積分で与えられる。XXZ模型には、XX模型には出てこなかった積分核が現れるために、それぞれ解析すべき関数に変形が加えられる。また、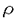 ( ( )やその微分に対する拘束条件より一連の方程式が与えられる。これらから、固有値を特徴的な関数Q+(k)の積分によって表すことが出来る。積分は留数計算によって与えられ、個々の留数が低温展開と解釈できる温度依存性を持つ。従来の計算では、このうち最初の1項だけを与えていたものと考えられる。 )やその微分に対する拘束条件より一連の方程式が与えられる。これらから、固有値を特徴的な関数Q+(k)の積分によって表すことが出来る。積分は留数計算によって与えられ、個々の留数が低温展開と解釈できる温度依存性を持つ。従来の計算では、このうち最初の1項だけを与えていたものと考えられる。 本論文の主要な成果をまとめる。 1.XX模型に対して、オイラー・マクロウリン公式を用いた自由エネルギーの低温展開の式を与えた。(第4章) 2.XXZ模型に対する自由エネルギーの低温展開を異方性パラメーター△=-cos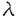 に関して、T3(for に関して、T3(for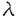 > >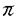 /3)、 /3)、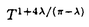 (for (for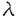 < <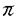 /3)まで求めた。(第5章) /3)まで求めた。(第5章) 3.XXX模型に対する自由エネルギーおよび相関長の低温展開を、T/log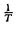 まで求めた。(第6章) まで求めた。(第6章) 4.オイラー・マクロウリン公式の高次微分項をとり入れることにより、熱力学的関数および相関関数に対して系統的な低温展開が行なえることを示した。(第4、5章) 以上のように、有限温度におけるハイゼンベルグ模型の物理的諸量を解析的に計算する系統だった方法を確立した。この方法はベーテ仮説法で解ける系に対して一般的に用いることが可能であると思われる。また、低温展開の各次数が特異点の解析により見通しよく求めることが出来ることを示した。これにより広く使われるオイラー・マクロウリン公式の有効性の確認も行った。オイラー・マクロウリン公式の使用に対してはMに関する収束性に疑問が投げかけられていたが、本論文ではXX模型とXXZ模型に対して詳細な解析を行ない、オイラー・マクロウリン公式が正しい低温展開を与えることを示すことができた。模型は限られているものの、オイラー・マクロウリン公式によって系統的な低温展開が正しく導出できることを初めて示した。また、XXX模型における低温展開にlogTを含む項が存在することを厳密計算により示したことは新しい。 |