水平面形状が三角形である三角形潜堤は、波高を減衰させることのみならず、波向を変えること、そして、その結果、沿岸流を制御することに対しても有効である。また、潜堤は、波を分裂させるから、波の周期の制御の可能性も秘めている。ところで、こうした波の分裂は、非線形性の強い場において生じる現象である。また、非線形系としての水の波は、媒質の輸送、すなわち、定常流の成分を含み得る。従って、三角形潜堤周辺の波または流れの場をより正確に解析するためには、波のいわゆる非線形性と分散性とを十分に考慮した基礎方程式を用いることが必要である。そこで、第1部において、次の2点を意図する。

　(1)強非線形・強分散性の波動方程式を基礎方程式として適用する、波・流れ場の平面2次元的な数値解析手法を提案する。

　(2)そして、この解析手法により、三角形潜堤の無限堤体列周辺の波・流れ場を対象として、数値実験を行なう。

　ところで、波浪に対する潜堤の影響をより大きくしようとして、天端高を上げたり、また、同じような大きさの潜堤をより岸近くに設置すると、潜堤上において砕波が起きるようになる。更に、沿岸流の制御を目的として三角形潜堤を用いるといった場合、潜堤の設置場所を砕波帯内にするのが得策の一つかも知れない。すなわち、砕波を扱えてこそ、潜堤による、より効果的な波浪制御、並びに、海浜流の制御にまで言及できるようになるのである。従って、第2部において、次の2点を目的とする。

　(1)第1部において提案した解析手法を拡張し、砕波が考慮できるようにする。

　(2)そして、三角形潜堤の堤体列が有する波・流れ場の制御機能について、砕波を含めて検討する。

　以上の議論で適用する波動方程式は、非回転運動に対して導かれたものである。従って、渦度の存在が無視し得ない場合には、これを基礎方程式として用いることができない。そこで、第3部において、対象とする流体は、同様に非圧縮性の完全流体であるが、その運動が回転であるときにも適用可能な、強非線形・強分散性の波動方程式を新たに導出する。

　このように、本論文は、3部構成となっている。

　第1部では、まず、波・流れ場の平面2次元的な非線形数値解析手法を提案する。

　すなわち、1.1で、第1部の序論を述べてから、1.2で、基礎方程式について述べる。近年、平面2次元の強非線形・強分散性の波動方程式が、複数の研究者によって開発され、それぞれの方程式の特徴も含めて、研究が蓄積されつつある。ここでは、非圧縮性の完全流体の非回転運動を対象とし、基礎方程式として、変分原理による平面2次元の強非線形・強分散性の波動方程式を用いる。その導出過程において、鉛直方向の積分を解析的に行なうが、その際に、速度ポテンシャルを鉛直分布関数の重み付き重ね合わせとして、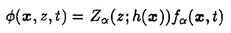のように表わす。の関数形は、が完全な級数となるように、対象に応じて適当に選択する。その項数は、高々数項しかとらないが、各項を連成振動させるから、このの近似の精度内で、流体運動の非線形性を十分に考慮することができる。鉛直分布関数の重み係数と水面変動が、求めるべき未知変数となる。

　なお、現在の所、強非線形・強分散性の波動方程式を平面2次元の波浪場に実際に適用した研究例は、あまりない。主として、水平床上におけるソリトンの衝突や潜堤上における波の分裂及び一様勾配斜面上における波の浅水変形といった現象の再現が、1次元問題の範囲内で試みられている段階である。本研究では、平面2次元の波浪場の解析を行なう。更に、波に伴う流れの解析も行なおうとする。

　ここで用いる波動方程式は、連立2階非線形偏微分方程式であるが、時間に関する微分項としては、線形な1階の微分項のみを含む。従って、数値解析においては、適当な初期条件から出発して、水平方向の境界条件を用いながら、時間の経過とともに差分方程式を解いていけばよい。1.3で、波動方程式を解く際に必要な、初期条件及び水平方向の境界条件について述べる。すなわち、次のような条件を適用する。

　(1)初期条件は、静水状態とする。

　(2)水平方向の境界には、側方境界,沖側境界及び岸側境界がある。このうち、側方境界には、同一の物理現象が、ある一定の長さの周期で沿岸方向に無限回繰り返しているという状況を想定し、周期境界条件を適用する。その際に、側方境界における速度ポテンシャルの多価性を認める。

　(3)他方、波が入射して来る沖側境界及び透過して行く岸側境界では、相対水深が深いという仮定のもとに、線形の開境界条件を適用する。

　そして、1.4で、数値計算法について述べる。波動方程式を差分方程式に離散化するにあたり、次のような方法を用いる。

　(1)ADI法を用いる。

　(2)空間に関しては、中央差分を用いる。

　(3)時間に関しては、に対して、中央型スキームまたは後退型

　スキームを用いる。従って、に対しては、陰解法を用いることになる。一方、に対しては、前進型スキームを用いる。従って、に対しては、陽解法を用いることになるため、この方法では、計算時間間隔△tをあまり大きくとれないという制約が課される。

　次に、本解析手法を三角形潜堤の無限堤体列周辺の波・流れ場に適用して、実際に数値計算を行なう。三角形潜堤周辺の波・流れ場について、波の非線形性までも厳密に考慮した解析は、いまだ行なわれていない。

　まず、1.5で、三角形潜堤による波・流れ場の制御の定性的な特徴を挙げる。

　そして、1.6で、比較的簡単な場合に対して、本解析手法の妥当性を確認してから、数値実験を行なう。数値実験において、同一の三角形潜堤が沿岸方向に無限に続く堤体列周辺の、波・流れ場を対象とする。その際、水深が一様な海域に、側面が緩やかな勾配からなる三角形潜堤を設置する。そして、緩勾配近似が成り立つ場合の波動方程式を適用する。微小振幅の規則波を入射させるが、その入射波の条件を変えて、それぞれの場合に波・流れ場がどのようになるかを調べる。入射波の条件としては、波向,周期及び波高があり、沖側境界における静水深を固定したとき、これらの条件によって、入射波が定まる。数値実験(I)では、これらの条件のうち、入射波の波向のみを変えて、波が潜堤上で全反射しない場合と全反射する場合の比較を行なう。また、入射波の波向が同じでも、周期によっては、波が潜堤上で全反射したりしなかったりする。数値実験(II)では、入射波の周期のみを変えて、それぞれの場合の比較を行なう。

　数値解析において、潜堤周辺の任意の時刻における水面波形及び速度ポテンシャルを求める。これより、水面波形の方向スペクトルが求まるから、波の屈折,反射及び分裂の様子がわかる。更に、計算結果を波高及び鉛直平均流速の定常流成分という、平面2次元的な時間平均値で評価する。

　1.7で、第1部の結論を述べる。

　第2部では、第1部で提案した解析手法を拡張して、砕波が考慮できるようにする。

　まず、2.1で、第2部の序論を述べる。いわゆる海浜流は、砕波に起因する。すなわち、砕波が、強制的に波の場を空間的に不均一な状態にすることによって生じる流れが、海浜流である。従って、砕波帯近傍においては、砕波に起因する波の不均一性による流れと波の非線形性による流れとが共存する。ここでは、次のような仮定のもとで、砕波を扱う。

　(1)砕波した波では、流体が有するエネルギーの一部が、水平渦の運動エネルギーや乱れのエネルギー等に供給される。ここでは、こうした現象を運動量の拡散として記述する。すなわち、砕波に伴う運動量の拡散を表わす砕波拡散項を波動方程式に付加する。

　(2)この砕波拡散項は、進行波を対象として定式化するが、ここでは、進行波性と重複波性のどちらの重合波浪場においても、同じ砕波拡散項を用いることにする。

　2.2で、砕波拡散項-_D∇²fの拡散係数_Dをモデル化する。_Dは、波高水深比を含むが、この波高として、第1部で定義したH_rmsを用いる。そして、分裂した波を含む場における波の周期として、入射波の周期を採用し、その1周期間における波高をH_rmsとする。

　次に、2.3で、_Dが含む係数について詳述する。は、波高水深比の空間的な変化を_Dの値に反映させるための係数である。によって、砕波に伴う拡散が生じる領域及び波の再成領域、更に、2次砕波以降の砕波に伴う拡散が生じる領域が、自動的に定まる。

　そして、2.4で、砕波拡散項を付加した波動方程式を解くための数値計算法について述べる。そこで用いる差分法は、第1部の方法に準じる。

　2.5で、ここで提案した解析手法を用いて数値計算を行なう。三角形潜堤を沿岸方向に無限個並べた堤体列が有する、波・流れ場の制御機能について検討する。その際に、第2部では、対象領域内で砕波が生じるようなモデル・ケースを設定して、数値実験を行なう。数値実験(III)では、潜堤上の天端水深のみを変えて、波が潜堤上で砕波しない場合と砕波する場合の比較を行なう。計算結果は、波高H_rms及び鉛直平均流速の定常流成分によって整理する。また、数値実験(IV)では、数値実験(II)の、入射波の周期が異なるそれぞれの場合において、入射波の波高を大きくし、潜堤上で波が砕波する条件を扱う。

　2.6で、第2部の結論を述べる。

　第3部では、流体運動が回転である場合にも適用可能な、非圧縮性の完全流体に対する平面2次元の強非線形・強分散性の波動方程式を導く。その導出方法は、第1部及び第2部で用いた波動方程式と同様であるが、流速の渦度成分を考慮するために、更に、2個の鉛直分布関数を導入する。

　以上より、本論文において、次のような結論を得た。

　(1)波の強非線形性・強分散性を考慮した、波・流れ場の平面2次元的な数値解析手法を提案した。基礎方程式に砕波拡散項を導入しているから、砕波も考慮可能である。

　(2)提案した数値モデルを適用することによって、微小振幅の規則波が入射するときの、三角形潜堤の無限堤体列周辺の波・流れ場の解析を行なった。

　(3)三角形潜堤上で、波が全反射しない場合、波の屈折の様子を水面波形の方向スペクトルを用いて定量的に把握した。また、波の屈折及び分裂により、堤体直後のある区間を除いて、波高が減衰した。

　(4)三角形潜堤上で、波が全反射する場合、潜堤の岸側斜辺付近の天端上で波高が局地的に非常に大きくなるが、堤体背後のある区間を除いて、波高が減衰した。また、潜堤背後において、波高の別のピークが現れる地点があった。ただし、光のように顕著な全反射は、起きなかった。

　(5)周期が長く、波長が潜堤の大きさの2倍もあるような波は、潜堤の影響を受けにくく、潜堤による制御が難しい。

　(6)潜堤上の砕波は、波が潜堤上で全反射するしないに関わらず、潜堤上及び潜堤背後において、波高の減衰効果を大きくし、定常流を減少させた。

　(7)潜堤上では、定常流が比較的大きくなるため、ここで行なったように、波と流れの相互干渉を両者の非線形性を十分に考慮して考える必要がある。

　(8)流体運動が回転である場合にも適用可能な、非圧縮性の完全流体に対する平面2次元の強非線形・強分散性の波動方程式を新たに導出した。

　本論文は、波浪制御構造物の一つとして最近着目されている三角形平面断面の潜堤列周辺の波・流れ場を対象として、従来に比し精度のより高い非線形数値モデルを提案し、それを用いた計算結果に基づいて潜堤列の波・流れに対する影響を論じたものであり、3部構成となっている。

　第1部は「三角形潜堤周辺の波・流れ場の非線形数値計算」と題する。先ず「序論」として、対象とする三角形潜堤周辺等の平面2次元波・流れ場の非線形数値解析に適用可能性のある各種手法についてのレヴューから、磯部により提案された非線形緩勾配方程式が最も相応しいと結論づけるとともに、第1部の内容を略述している。これに続く3つの章では、「基礎方程式」、「初期条件及び水平方向の境界条件」、「数値計算法」のそれぞれについて、基礎となる波動方程式の導出から始めて初期・境界条件式ならびにそれらの差分化と差分方程式の吟味を行って、砕波を考慮しない場合の数値計算法を提案している。特に沿岸方向の境界条件に関しては、潜堤列まわりの波と流れの正しい解を得るための速度ポテンシャルに対する多価性を考慮した条件式を新たに提示したことが1つの成果として評価できよう。

　次いで「三角形潜堤による波・流れ場の制御」の章で三角形潜堤が有する波高・波向・周期および流れ場の制御機能を説明した後、次章「三角形潜堤周辺の波・流れ場の数値実験」においては、各種条件の下での無限列潜堤周辺の波・流れ場の数値計算結果に基づいて、波が光学的全反射をしない場合について波の屈折ならびに潜堤上の分裂による2倍周波数成分の発生、および全反射条件の場合も含めて波高分布の特性を明らかにした。また潜堤上と周辺の流れの計算結果についても論じ、特に潜堤上では平均流の流速が相当に大きくなることから、本計算手法のように非線形性を充分に考慮した扱いが不可欠であるとの結論を得ている。

　第1部は「三角形潜堤を用いた砕波を伴う波・流れ場の制御」と題する。ここでは先ず、三角形潜堤周辺の波・流れ、特に潜堤背後の海浜流を実務に応用可能な条件で解析するためには潜堤上での砕波を包含した波・流れ場の数値モデルが必須であることを「序論」において述べ、その基礎となる考え方を示している。これを受けて次の2章「砕波に伴う運動量の拡散のモデル化」および「砕波拡散項中の係数の意味」においては、砕波現象に起因する水平渦・乱れへの波からのエネルギー移行を水平運動量の拡散として解釈し、非線形緩勾配方程式に付加すべき運動量拡散項を導出している。基本となるアイデア自体は斬新なものではないが、運動量拡散項を非定常緩勾配方程式に導入する試みは従来の研究ではなされていなかったもので、現段階では最も新しくかつ合理的な扱いとして高く評価できるものである。また、従来は別途に経験式等によって決定していた砕波点位置の判定を運動量拡散項の算定の中で行う手法を提案しており、これにより従来行われていた運動量拡散項中の係数の人為的な漸増を不必要とすることに成功している。本研究で対象としているような重複波性の砕波と砕波減衰も生じうる条件にまで同一の扱いを援用している点には問題があるが、重複波性砕波に対する現状の我々の理解の段階からすれば、やむを得ないものと判定される。

　次いで「数値計算法」の章で具体的な差分式と計算法を示した後、「三角形潜堤を用いた砕波を伴う波・流れ場の制御」の章で数値解析結果について議論を行っている。数値解析では、三角形潜堤の天端水深と入射波の周期を独立に変えるとともに、入射波高をも変えて砕波・非砕波の両条件に対する計算を行っており、その結果として、潜堤上で砕波する場合には、全反射条件を満たすか否かに関わらず、潜堤上とその背後においては、非砕波の場合に比べて波高の減衰効果が大きく、流れも弱くなることが見いだされた。

　最後の第3部は「非圧縮性の完全流体に対する平面2次元の強非線形・強分散性の波動方程式」と題する。ここでは、非線形緩勾配方程式等の従来の波動方程式とは異なり、流体運動が回転性である場合にも適用可能な非圧縮完全流体に対する平面2次元の強非線形・強分散性の波動方程式を新たに導いている。定式化自体は非線形緩勾配方程式に対するものに準ずるが、流速の渦度成分をも包含するために、更に2個の鉛直分布関数を用いて表現している。これらの鉛直分布関数を合理的に決定するためには砕波のプロセスに関するより詳細な知見を必要とするため、直ちに波・流れの解析に応用することは現状では残念ながら無理であるが、砕波変形に対する今後の研究に寄与するところは大である。

　以上を要するに、本論文は、波浪制御構造物としての三角形平面断面潜堤列周辺の砕波を伴う波・流れ場に関して、より信頼性の高い数値計算モデルを提示し、かつ潜堤周辺の波・流れ場の特性を明らかにしたものであり、海岸工学上貢献するところが大きい。よって、本論文は博士(工学)の学位請求論文として合格と認められる。