学位論文要旨
| No | 112900 | |
| 著者(漢字) | 赤堀,次郎 | |
| 著者(英字) | Akahori,Jiro | |
| 著者(カナ) | アカホリ,ジロウ | |
| 標題(和) | 数理ファイナンスに関係する確率論の諸問題 | |
| 標題(洋) | SOME PROBLEMS OF STOCHASTIC CALCULUS RELATED TO METHEMATICAL FINANCE | |
| 報告番号 | 112900 | |
| 報告番号 | 甲12900 | |
| 学位授与日 | 1997.03.28 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(数理科学) | |
| 学位記番号 | 博数理第71号 | |
| 研究科 | 数理科学研究科 | |
| 専攻 | ||
| 論文審査委員 | ||
| 内容要旨 | 本論文においては(i)Ritchken and Sankarasubramanian[17][18]型の金利期間構造のモデルと、(ii) 以下では( Propsition1.1. ここで、E*(・)はP*に対する期待値 で与えられるが、このとき、右辺の条件つき期待値がrt(と幾つかの状態変数)の簡単な関数でかかれていることが望ましい。これはrtをマルコフ過程とすることが1つの解決法であるが、本論文では単に連続マルチンゲールを基礎に次のようなモデルを考えた。 すると Proposition1.4. を得る。 (ただしここで (0.2)の式を方程式で与えようとすれば、例えば となるが、 Theorem3.1. Theorem4.2. ただし、ここでeは、Xの無限大への到達時刻、すなわち爆発時刻である。 Theorem3.1の証明は、 というスケール変換を用いて1次元マルコフ型の評価に持ち込むことによってなされる。 Theorem4.2の証明は、 として、Atによる時間変更をXに対して施した確率過程Ytを考えることによってなされる。 すなわち、 であり、(0.9)の右辺第2項はFAtに適合したブラウン運動であることにより、結局、Yは、 の解となる。(ここでBは新しいブラウン運動である。) この方程式を変形して、 とし、Bをノイズとみなして、常微分方程式だと思うことにする。以下、そもそもslowly varying functionは、無限大の近傍でのみ決まるのであるから、law of iterated logarithmとあわせて、比較定理を繰り返し用いることにより、Theoremを得る。 本論文の後半は Theorem5.1. ここで、 である。 証明はFeynman-Kacの公式を用いてなされる。また、これを直接 Theorem8.1(Dassios[4]). という表現を得る。これについて若干の考察が本論文セクション7と8で与えられている。 | |
| 審査要旨 | 本論文では数理ファイナンスに関する2つの話題(i)金利のモデルと期間構造(ii) まず金利モデルについての結果を述べる。(
と定める。この時次の事実が成立する。 定理1適当な可積分条件の下で
確率測度Pをリスク中立確率と考え、
と表される。よって上記の定理よりlog p(t,T)は このようなモデルは特殊な場合がRitchken-Sankarasubramanianにより与えられていた。しかし、彼らの結果は可積分性のチェックが十分でない。上の特別な場合として次のような確率積分方程式を考える。
ただし、Wtはブラウン運動。この時、次の結果が成り立つ。 定理2とする。のとき、(1)の解は確率1で有限時間に爆発する。 定埋3
ならば、(1)の解は確率1で有限時間に爆発する。
ならば、(1)の解は確率1で爆発しない。 爆発が起こるときは可積分条件が崩れるので、モデルとして不適当である。上記の結果はこのような数理ファイナンス上の意味があるが、数学的結果としてもぎりぎりの条件を出しているので興味深いものである。 本論文の後半は 定理4
ここで、
である。 上記の結果を用いて 以上のように本論文は独創性のあるきわめて質の高いもので、論文提出者赤堀次郎は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/54598 |
 -パーセンタイル・オプションの価格の数学的側面が議論される。(i)に関して、より一般的なモデルを与え、その数学的構造を明らかにし、(Proposition1.4)さらに、関係する確率積分方程式の解の爆発条件があたえられる(Theorem3.1,4.2)。これはモデルの妥当性に深く関係する(Remark1.5,1.6)。(ii)に関しては、ドリフトのついたブラウン運動にかんする逆正弦法則をもとめている(Theorem5.1)。それを用いて、
-パーセンタイル・オプションの価格の数学的側面が議論される。(i)に関して、より一般的なモデルを与え、その数学的構造を明らかにし、(Proposition1.4)さらに、関係する確率積分方程式の解の爆発条件があたえられる(Theorem3.1,4.2)。これはモデルの妥当性に深く関係する(Remark1.5,1.6)。(ii)に関しては、ドリフトのついたブラウン運動にかんする逆正弦法則をもとめている(Theorem5.1)。それを用いて、 ,F,P,{Ft}t∈[0,∞))を適当な確率空間の4つ組みとし、同値マルチンゲール測度とよばれるP*の存在を仮定し、(ある種の経済学的均衡の概念と同値であることが知られているc.f.Harrison and Pliska[8],Duffie[6])WをP*-ブラウン運動とする。
,F,P,{Ft}t∈[0,∞))を適当な確率空間の4つ組みとし、同値マルチンゲール測度とよばれるP*の存在を仮定し、(ある種の経済学的均衡の概念と同値であることが知られているc.f.Harrison and Pliska[8],Duffie[6])WをP*-ブラウン運動とする。 t,t∈[0,∞)(連続正値{Ft}t∈[0,∞)-適合過程)を瞬間的短期金利としたとき、満期がTである債権の時刻tでの価格p(t,T)は、
t,t∈[0,∞)(連続正値{Ft}t∈[0,∞)-適合過程)を瞬間的短期金利としたとき、満期がTである債権の時刻tでの価格p(t,T)は、




 ,
, はdeterministicな過程である。)
はdeterministicな過程である。)
 (x)のx無限大でのオーダーが、
(x)のx無限大でのオーダーが、 より大きいと、(0.6)のドリフト項がlinear growth conditionを破ることになる。しかし、数理ファイナンスにおいてはそういうものがよく扱われるので、詳しく調べる必要がでてくる。結果は、
より大きいと、(0.6)のドリフト項がlinear growth conditionを破ることになる。しかし、数理ファイナンスにおいてはそういうものがよく扱われるので、詳しく調べる必要がでてくる。結果は、 とする。
とする。 のとき、(0.6)の解は確率1で爆発する。
のとき、(0.6)の解は確率1で爆発する。 とする。ここでL(x)はslowly varying functionである。
とする。ここでL(x)はslowly varying functionである。


 の逆関数をAt、すなわち、
の逆関数をAt、すなわち、
 である。このとき、
である。このとき、
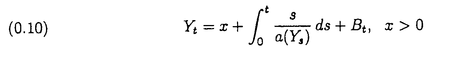

 >0に対して、
>0に対して、
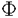 は正規分布の末尾の分布関数、すなわち
は正規分布の末尾の分布関数、すなわち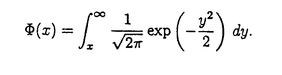

 t,t∈[0,∞)は連続でdeterministicな関数とし、、
t,t∈[0,∞)は連続でdeterministicな関数とし、、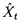 と[M]tの簡単な関数となるので、実務上有用なモデルと考えられる。
と[M]tの簡単な関数となるので、実務上有用なモデルと考えられる。