| 内容要旨 | | この論文に於いて,筆者は符合(2,1)の実ユニタリー群SU(2,1)の標準表現に対する一般化ホイタッカー関数の明示公式及び,一般化ホイタッカー模型の一意性を示した.以下その動機と詳細を述べる. 保型形式の研究に於いて,そのフーリエ展開は基本的かつ重要な役割を担っている.しかしながら,現状の多変数保型形式論に於けるフーリエ展開の理論は未だ満足のゆくものから程遠い. Gを簡約群,Fをその上の保型形式,それを含むGの保型表現を とする時,Fのフーリエ展開を考察する事は表現論的には, とする時,Fのフーリエ展開を考察する事は表現論的には, のNへの制限 のNへの制限 |Nの既約分解を研究することである.ここで,Nは,Gの放物型部分群の冪零根基を表す.Fのホイタッカー関数とは,Nの指標 |Nの既約分解を研究することである.ここで,Nは,Gの放物型部分群の冪零根基を表す.Fのホイタッカー関数とは,Nの指標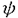 に対してHomN( に対してHomN( |N |N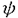 ),あるいはフロベニウス相互律により ),あるいはフロベニウス相互律により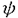 のGへの誘導表現 のGへの誘導表現 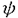 を使ってこれと同型な絡空間HomG( を使ってこれと同型な絡空間HomG( , , 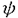 )を考え,それに属する絡作用素(ホイタッカー汎関数と呼ばれる)の像を指す.その像全体の張る空間を )を考え,それに属する絡作用素(ホイタッカー汎関数と呼ばれる)の像を指す.その像全体の張る空間を のホイタッカー模型と呼び,dimCHomG( のホイタッカー模型と呼び,dimCHomG( , , 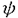 )=1が成り立つ時, )=1が成り立つ時,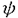 のホイタッカー模型は一意であると言う.しかるに のホイタッカー模型は一意であると言う.しかるに のNへの制限 のNへの制限 |Nの既約成分にはNが可換群でない限り,一般には指標以外にも高次元の表現が現れる.従って,保型形式Fの完全なフーリエ展開の記述は,ホイタッカー関数のみでは望むべくもない。そこで,素朴な問題設定として,Nの任意のユニタリー表現 |Nの既約成分にはNが可換群でない限り,一般には指標以外にも高次元の表現が現れる.従って,保型形式Fの完全なフーリエ展開の記述は,ホイタッカー関数のみでは望むべくもない。そこで,素朴な問題設定として,Nの任意のユニタリー表現 に対して,HomG( に対して,HomG( , ,  )を研究する事が考えられる. )を研究する事が考えられる. 筆者はGがSU(2,1)の場合にこの問題を考察した.この時,放物型部分群は同型を除いて唯一つであり,その冪零根基Nは三次元ハイゼンベルグ群に同型となる.従ってそのユニタリー表現の同型類の代表は,ストーン・フォンノイマンの定理により,指標を除いては,中心指標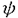 sで決定される無限次元表現 sで決定される無限次元表現 で尽くされる.指標に対しては,織田・古関両氏の研究でホイタッカー関数の明示公式が得られている[K-O].残る問題は,無限次元表現 で尽くされる.指標に対しては,織田・古関両氏の研究でホイタッカー関数の明示公式が得られている[K-O].残る問題は,無限次元表現 の場合である.しかし,今の場合HomG( の場合である.しかし,今の場合HomG( , , 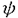 )を考察するのは,正しい方針ではない.実際,この空間は一般に無限次元であり,一意性は成り立たない.問題の正しい定式化には,Nを含む少し大きな群Rを導入し.被約ゲルファント-グラーエフ表現 )を考察するのは,正しい方針ではない.実際,この空間は一般に無限次元であり,一意性は成り立たない.問題の正しい定式化には,Nを含む少し大きな群Rを導入し.被約ゲルファント-グラーエフ表現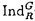  を考察する必要がある. を考察する必要がある. Pのレヴィ分解をL.Nとする.LはNへ共役で作用しており,その作用は,Nのユニタリー表現の同型類のなす集合 へ自然に延びる.SをLに於けるNの中心Z(N)に自明に作用する最大の閉部分群とすると, へ自然に延びる.SをLに於けるNの中心Z(N)に自明に作用する最大の閉部分群とすると, は中心指標 は中心指標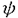 sのみで決まるので,Lに於けるその固定化群はSに一致する.ここで,半直積S.NをRとおき,Nの無限次元表現 sのみで決まるので,Lに於けるその固定化群はSに一致する.ここで,半直積S.NをRとおき,Nの無限次元表現 をRへ自然な方法で延長した表現を をRへ自然な方法で延長した表現を とする.HomG( とする.HomG( , ,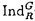  )を一般化ホイタッカー汎関数の空間,その元の像Wを一般化ホイタッカー関数と呼ぶ.この論文に於いて筆者は山下氏の結果[Ya]をもとに[K-O]に従い具体的に一般化ホイタッカー関数Wの動径成分W|Aの満たす微分方程式を導出した.これを解くことにより, )を一般化ホイタッカー汎関数の空間,その元の像Wを一般化ホイタッカー関数と呼ぶ.この論文に於いて筆者は山下氏の結果[Ya]をもとに[K-O]に従い具体的に一般化ホイタッカー関数Wの動径成分W|Aの満たす微分方程式を導出した.これを解くことにより, が離散系列表現の時は が離散系列表現の時は の極小K-タイプに属するWの, の極小K-タイプに属するWの, が主系列表現の時はその"角の"K-タイプに属するWの動径成分W|Aの明示公式を得,同時に一意性定理を証明した.ここにKはGの極大コンパクト部分群,Aはベクトル群を表す. が主系列表現の時はその"角の"K-タイプに属するWの動径成分W|Aの明示公式を得,同時に一意性定理を証明した.ここにKはGの極大コンパクト部分群,Aはベクトル群を表す.  を を のK-タイプ,即ち次の分解に現れるKの表現とする. のK-タイプ,即ち次の分解に現れるKの表現とする.  但し はKの既約表現の同型類のなす集合を表す.この時,K-同変埋め込み はKの既約表現の同型類のなす集合を表す.この時,K-同変埋め込み : : → → により, により,  とK-タイプを指定し,次の同型  但し  に注意する.S(R)は表現 のC∞-ベクトルの全体としてシュワルツ関数の成す空間である.K-タイプが のC∞-ベクトルの全体としてシュワルツ関数の成す空間である.K-タイプが である一般化ホイタッカー関数Wは上の空間 である一般化ホイタッカー関数Wは上の空間 に属しており,その動径成分W|Aのみで決定される.この動径成分W|Aは定数倍を除いて次のように与えられる. に属しており,その動径成分W|Aのみで決定される.この動径成分W|Aは定数倍を除いて次のように与えられる. 主定理W|Aを,SU(2,1)の標準表現 に対するK-タイプ に対するK-タイプ の一般化ホイタッカー関数の動径成分とする. の一般化ホイタッカー関数の動径成分とする. i) が離散系列表現の時. が離散系列表現の時. は は の極小K-タイプとし,そのブラットナーバラメターを( の極小K-タイプとし,そのブラットナーバラメターを( 1. 1. 2)とする. 2)とする. i-1) :大きな離散系列表現の場合 :大きな離散系列表現の場合  但し, とmはk,s, とmはk,s, 1, 1, 1,…で記述されるパラメター. 1,…で記述されるパラメター. i-2) :正則離散系列表現の場合 :正則離散系列表現の場合  但し,s<0. i-3) :反正則離散系列表現の場合 :反正則離散系列表現の場合 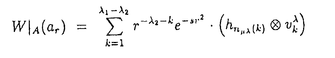 但し,s>0. ii) が主系列表現の時. が主系列表現の時. は は の"角の"K-タイプとする. の"角の"K-タイプとする.  但し, とmはk,s,v,…で記述されるパラメター. とmはk,s,v,…で記述されるパラメター. ここで,{hn:n∈N}と{ k:k=0,…, k:k=0,…, 1- 1- 2}は,各々 2}は,各々 と と の表現空間の基底を表す. の表現空間の基底を表す. また,hnはエルミート関数を, はRe(m- はRe(m- + + )>0かつx>0に於いて )>0かつx>0に於いて  という積分表示を持つ古典的なホイタッカー関数を表す.変数arはAの元  である. 系動径成分が緩増加であるベクトル全体のなす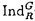  の部分空間を の部分空間を とする. とする. *から *から への(gC,K)-加群としての絡作用素全体の成す空間の次元は1以下である. への(gC,K)-加群としての絡作用素全体の成す空間の次元は1以下である. [K-O]Koseki,H.and Oda,T., Whittaker functions for the large discrete series representations of SU(2,1)and related zeta integral, Publ.RIMS Kyoto Univ.,31(1995),959-999. [Ya] Yamashita,H.,Embedding of discrete series into induced representations of semisimple Lie groups II:Generalized Whittaker models for SU(2,2),J.Math.Kyoto Univ.,31-1(1991),543-571. |