| 内容要旨 | | この論文の主目的は,いくつかの実半単純Lie群に対応した旗多様体上の各軌道に対し,その余法束のモーメント写像による像を,具体的に決定することである.本論文では不定値ユニタリ群U(p,q),実斜交群Sp(n,R),不定値斜交群Sp(p,q)に対応する場合を扱っている. この問題を考える動機を実半単純Lie群の表現論から説明しよう.実半単純Lie群の表現に対し,その随伴多様体は重要な表現の不変量である.一方,実半単純Lie群GRの自明な無限小指標をもつ既約Harish-Chandra加群はBeilinson-Bernstein対応によってホロノミックD-加群と対応している[1].更に,表現に対応するこのD-加群はRiemann-Hilbert対応によって既約なperverse sheafと対応し,これはGR 複素化の旗多様体上のGRの極大コンパクト部分群の複素化によるある軌道の上のlocally constant sheafに関するintersection complexであるという意味で,旗多様体上の軌道と対応することが知られている.このD-加群と随伴多様体との対応はBorho-Brylinski[2]によってなされており,表現(Harish-Chandra加群)の随伴多様体はBeilinson-Bernstein対応によって対応するD-加群の特性多様体のモーメント写像による像と一致する.特に,離散系列表現の場合は,D-加群の特性多様体は旗多様体の対応する閉軌道の余法束に一致するので,随伴多様体は,この余法束のモーメント写像による像に他ならない.このモーメント写像による像を,旗多様体上の全ての軌道に対し具体的に決定する. ここで少し記号を用意する.GRを実古典群とし,GRの極大コンパクト部分群の複素化をKとする.KのLie環を とし, とし, のGのLie環g内の直交補空間をpとしよう.旗多様体上のK-軌道の余法束のモーメント写像による像は,pの巾零元からなるK-不変な部分集合であり,しかも,この像の中で稠密なK-軌道が唯一つ存在する[2],[3].従って,この稠密な巾零K-軌道を決定すれば余法束のモーメント写像による像がわかったことになる.このようにして旗多様体上の各K-軌道から巾零K-軌道が一つ決まる.我々が書き下したいのはこの対応である.p上の巾零K-軌道は「符号付Young図形」(箱の中に一定のルールで+や-の記号を入れたYoung図形)でパラメトライズされ,このYoung図形の形と符号から軌道の閉包間の包含関係も読み取ることができる[3].一方,旗多様体上のK-軌道については,松木,Rossmannが分類し[5],[7],[8],更に古典群に対しては,松木-大島が旗多様体上K-軌道をパラメトライズするものとしてclanと呼ばれる記号を導入した[6]. のGのLie環g内の直交補空間をpとしよう.旗多様体上のK-軌道の余法束のモーメント写像による像は,pの巾零元からなるK-不変な部分集合であり,しかも,この像の中で稠密なK-軌道が唯一つ存在する[2],[3].従って,この稠密な巾零K-軌道を決定すれば余法束のモーメント写像による像がわかったことになる.このようにして旗多様体上の各K-軌道から巾零K-軌道が一つ決まる.我々が書き下したいのはこの対応である.p上の巾零K-軌道は「符号付Young図形」(箱の中に一定のルールで+や-の記号を入れたYoung図形)でパラメトライズされ,このYoung図形の形と符号から軌道の閉包間の包含関係も読み取ることができる[3].一方,旗多様体上のK-軌道については,松木,Rossmannが分類し[5],[7],[8],更に古典群に対しては,松木-大島が旗多様体上K-軌道をパラメトライズするものとしてclanと呼ばれる記号を導入した[6]. 本論文ではこの松木-大島の記号に基づいた旗多様体上のK-軌道の媒介記号を新しく導入し,代表元,軌道の次元,等を与えるとともに,媒介記号からモーメント写像による像を与えるアルゴリズムを与える.加えてこの結果を利用し,稠密に入っている巾零K-軌道に対応する符号付Young図形を決定する. 本論文では第1章でGRが不定値ユニタリ群U(p,q)の場合に対して上記のことを行ない,第2章,第3章ではそれぞれ群のU(n,n),U(2p’,2q’)の場合への「良い埋め込み」を実現し,実斜交群Sp(n,R),不定値斜交群Sp(p’,q’)の場合の結果を与える. U(p,q)の場合 まずGR=U(p,q)の場合,つまりG=GL(p+q,C),K=GL(p,C)×GL(q,C)の場合を扱う.GのBorel部分群をBとする. GL(p+q,C)の旗多様体X=G/Bは次のようなp+q個のベクトル空間の列からなる.  旗多様体上には自然に群Gが作用している.Cp+q=V+(+)V-をK-不変部分空間への直和分解(dimV+=p,dimV-=q)とすると,旗V=(V0,Vl,V2,…,Vp+q)に対する次の値はK-不変である.  本論文で与えた媒介記号はこれらの値により定まるp+q個の記号の列 =(C1,…Cp+q)であり,標記方法はMatsuki-Oshimaの与えた媒介記号に基づいている. =(C1,…Cp+q)であり,標記方法はMatsuki-Oshimaの与えた媒介記号に基づいている. Definition1.次の4つの条件を満たすp+q個の記号の列 =(C1…Cp+q)をU(p,q)のindicationと呼ぶ. =(C1…Cp+q)をU(p,q)のindicationと呼ぶ. 1.記号ciは+,-,または自然数N={1,2,…}の要素の1つである. 2.ci∈Nであったとき,Cj=Ciであるようなj≠iが一意に存在する 3.(c1…cn)内の+の個数と-の個数の差はGRを定義するHermitian形式の符号p-qに一致する. 4.ci∈N,a∈Nかつa<ciならばCj= であるようなjが存在する. であるようなjが存在する. つぎの同値関係により定まるindicationの同値類をclanと呼ぶ 2つのindication(C1…Cn)と(C’1…C’n)が同値であるとは,すべての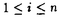 に対し, に対し,  を満たすある置換 ∈ ∈ m(ただし,m:=max{c’i∈N})が存在すること. m(ただし,m:=max{c’i∈N})が存在すること. U(p,q)に対するclanはU(p,q)に対する旗多様体上のK-軌道の媒介記号となる. 旗多様体X上のK-軌道Qに対し,その余法束 のモーメント写像 のモーメント写像 による像はK-軌道Qの余法束の1点x∈Qでのファイバーの像 による像はK-軌道Qの余法束の1点x∈Qでのファイバーの像 のK-saturationである.clanの記号から,この のK-saturationである.clanの記号から,この を与えるのが次の主定理である. を与えるのが次の主定理である. Theorem2(Theorem1.47).与えられたK-軌道Qに対応するclan =(c1…cp+q)に対し,signed clan =(c1…cp+q)に対し,signed clan =(d1…dp+q),置換 =(d1…dp+q),置換 ∈ ∈ p+q,代表元x=g( p+q,代表元x=g( )B∈XをDefinition1.17,Theorem1.22で定めると,signed clanに対しDefinition1.46で定まるgの部分空間Dri( )B∈XをDefinition1.17,Theorem1.22で定めると,signed clanに対しDefinition1.46で定まるgの部分空間Dri( )を )を で置換したものはK-軌道Qの余法束のxでのファイバーのモーメント写像による像 で置換したものはK-軌道Qの余法束のxでのファイバーのモーメント写像による像 である. である.  つまりDri( )の(i,j)-成分は )の(i,j)-成分は の( の( (i), (i), (j))-成分を表し,Dri( (j))-成分を表し,Dri( )の(i,j)-成分はsigned clanのi-成分とj-成分(とci=cs∈N,または,ci=ct∈Nだった時にはs-成分またはt-成分)とi,j(,s,t)の大小関係で決まる.さらに,この定理に基づいてsigned clanからDri( )の(i,j)-成分はsigned clanのi-成分とj-成分(とci=cs∈N,または,ci=ct∈Nだった時にはs-成分またはt-成分)とi,j(,s,t)の大小関係で決まる.さらに,この定理に基づいてsigned clanからDri( )を与えるアルゴリズムをDefinition1.50で与える. )を与えるアルゴリズムをDefinition1.50で与える. 特に,旗多様体上の閉軌道に対しては(つまり離散系列表現に対応する軌道に対しては)主定理は次のように簡潔になる. Corollary3. =(c1…cp+q)が閉軌道のclanであるとき,つまりci=+または-であるとき, =(c1…cp+q)が閉軌道のclanであるとき,つまりci=+または-であるとき, に対応するK-軌道の余法束のある1点でのモーメント写像による像 に対応するK-軌道の余法束のある1点でのモーメント写像による像 は次で与えられる. は次で与えられる.  ただし ∈ ∈ p+qは p+qは に対し定まる置換(Theorem 1.22). に対し定まる置換(Theorem 1.22). clanを使うと軌道の次元も次のように簡単な表示をもつ. Proposition1.32.clan =(c1…cn)の長さl( =(c1…cn)の長さl( )を定義しよう )を定義しよう  U(p,q)のclan =(c1…cn)とそれに対応する旗多様体上のK-軌道Qに対し,次元と余次元は次で与えられる. =(c1…cn)とそれに対応する旗多様体上のK-軌道Qに対し,次元と余次元は次で与えられる.  Sp(n,R)とSp(p’,q’)の場合 実斜交群Sp(n,R)と不定値斜交群Sp(p’,q’)は,それぞれ次のような関係が成り立つようにU(n,n)とU(2p’,2q’)に埋め込むことができる.(これが「良い埋め込み」である.)  ただし,ここでは斜交群に対するそれぞれの群はG’等のようにプライムをつけて表している.この実現を与え,U(p,q)の場合に埋め込んで扱うことで,それぞれの群の結果を具体的に与える.たとえば,G’R=Sp(n,R)に対す媒介記号generalized clanはGR=U(n,n)に対するclanの部分集合であり,G’R=Sp(p’,q’)に対するgeneralized clanはGR=U(2p’,2q’)に対するclanの部分集合である(Definition2.10,Definition3.7).ここではK’の作用によるC2nの不変直和分解C2n=V++V-がG’R=Sp(n,R)のとき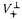 =V+, =V+, =V-を満たし,G’R=Sp(p’,q’)のとき =V-を満たし,G’R=Sp(p’,q’)のとき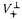 =V-を満たすことがポイントとなる.ここで与えられたgeneralized clanに対応するK’-軌道の余法束のある1点でのモーメント写像による像はU(p,q)の場合に与えられたもののg’への制限に他ならないことを利用して像である空間を与え(Proposition2.33,Proposition3.27),generalized clanを使っての旗多様体上のK-軌道の次元公式も与えている(Proposition2.32,Proposition3.26). =V-を満たすことがポイントとなる.ここで与えられたgeneralized clanに対応するK’-軌道の余法束のある1点でのモーメント写像による像はU(p,q)の場合に与えられたもののg’への制限に他ならないことを利用して像である空間を与え(Proposition2.33,Proposition3.27),generalized clanを使っての旗多様体上のK-軌道の次元公式も与えている(Proposition2.32,Proposition3.26). REFERENCES[1] A.Beilinson and J.Bernstein,Localisation de g-modules,C.R.Acad.Sci,Paris292(1981),Serie I,15-18.[2] W.Borho and J.Brylinski,Differential operators on homogeneous spaces.III,Invent.Math.,80(1985),1-68.[3] D.Collingwood and W.McGovern,Nilpotent orbits in semisimple Lie algebras,Van Nostrand Reinhold,New York,1993.[4]B.Kostant and S.Rallis,Orbits and representations associated with symmetric spaces,Amer.J.Math.,93(1971),753-809.[5]T.Matsuki,The orbits of affine symmetric spaces under the action of minimal parabolic subgroups,J.Math.Soc.Japan,31(1979),331-357.[6]T.Matsuki and T.Oshima,Embeddings of discrete series into principal series,The orbit Method in Representation theory,Progress in Math.,82(1988),Birkhauser,147-175.[7]W.Rossmann,The structure of semisimple symmetric spaces,Queen’s paper Pure Appl.Math.,48(1978),513-520.[8]D.Vogan,Irreducible characters of semisimple Lie groups III,Invent.Math.,71(1983),381-417. |