学位論文要旨
| No | 112906 | |
| 著者(漢字) | 熊ノ郷,直人 | |
| 著者(英字) | Kumano-go,Naoto | |
| 著者(カナ) | クマノゴウ,ナオト | |
| 標題(和) | フーリエ積分作用素の多重積について | |
| 標題(洋) | On multi-products of Fourier integral operators | |
| 報告番号 | 112906 | |
| 報告番号 | 甲12906 | |
| 学位授与日 | 1997.03.28 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(数理科学) | |
| 学位記番号 | 博数理第77号 | |
| 研究科 | 数理科学研究科 | |
| 専攻 | ||
| 論文審査委員 | ||
| 内容要旨 | j=1,2,…,L+1に対し、相関数 任意の非負整数l,l’に対し、ある正定数Cl,l’と正整数l1,l’1が存在して、 を満たす。ここで、 このFourier積分作用素の多重積の評価は、Fourier積分作用素の計算に有効である。[9],[10],[12]で、この評価は、双曲型のsystemに対する基本解の構成に用いられた。また、この評価を少し修正したものが、Schrodinger方程式の基本解の構成に用いられた。 Typeset by AMS-TEX (cf.D.Fujiwara[1]〜[4],H.Kitada and H.Kumano-go[8],N.Kumano-go[11])しかしながら、それらの証明は、まず表象1をもつFourier積分作用素の逆元を作り、それを用いて、それぞれのFourier積分作用素から擬微分作用素を作り、擬微分作用素の多重積の評価に持ち込むという間接的な方法を用いていた。特に、表象1をもつFourier積分作用素の逆元が存在するための相関数の条件は複雑であるため、この評価が成立するためには、相関数に対応する正準写像は恒等写像に非常に近くなければならなかった。最近、[5]で、D.Fujiwara,N.Kumano-goとK.Taniguchiは、Schrodinger方程式の場合に、この評価の、より直接的な証明を与え、相関数に対する条件を簡明にした。しかし、彼らは、もとの双曲型のsystemの場合には、成功していない。この論文の目的は、もとの双曲型のsystemの場合に、より直接的な証明を与え、相関数に対する条件を簡明にすることである。 もとのH.Kumano-go-Taniguchiの定理と、この論文の主定理の違いを正確に述べるために、H.Kumano-go-Taniguchi[9],[10],[12]のFourier積分作用素のいくつかの定義と命題を述べる。 [定義1] (表象の族 を満たすこととする。ここで、〈 p∈ で定義すると、 [定義2] (相関数の族 [定義3] (Fourier積分作用素I( で定義する。ここで、uは、Rn上の急減少C∞-関数とし、右辺の積分は、振動積分とする。 [命題4](相関数の積 (1)(x, は、ただひとつの解 (2)ある正定数の増加列 を満たす。ただし、 で定義された関数とする。ここで、 以上の定義と命題を用いて、この論文の主定理を述べると次のようになる。(本文では、もう少し一般的な形で述べている。) [主定理]. (1) を満たす。ここで、 (2)さらに、任意の非負整数l,l’に対し、ある定数Cl,l’が存在し、 を満たす。ただし、 (1)相関数の条件 (2)もとのH.Kumano-go-Taniguchiの証明は間接的であるがゆえ、l1,l’1は、もっと大きくとらねばならない。 | |
| 審査要旨 | 本論文提出者はフーリエ積分作用素の多重積に対し、結合して得られる同種の作用素の定量的性質、特にその表象の定量的評価を研究した。数理物理学などに現れる時間発展方程式、例えば波動方程式やシュレジンガー方程式は数学的にはそれぞれ、双曲型微分方程式、シュレジンガー型微分方程式に対する初期値問題として定式化され、解の存在、一意性、初期値に関する連続性などが広範に研究されてきた。一方、特にシュレジンガー方程式の一解法には、古典力学と量子力学との結びつきの数学的な根拠になった、物理学者ファインマンによる経路積分による解の表示法がある。この方法は現在、無限自由度の量子系である場の量子論にも引き継がれ素粒子論から位相幾何学に及ぶまで大きな影響を与えている。経路積分法をより一般的な偏微分方程式の解の表示理論として抽象化したものがフーリエ積分作用素とその多重積の理論である。 フーリエ積分作用素I(
であって、
の母関数と呼ばれる。実際、このGはf(x)と(I(
を一つのフーリエ積分作用素I(
によいノルム評価:任意の非負整数l,l’に対し、ある正定数Cl,l’と正整数l1,l’1が存在して、
を与えたことである。ここで 本論文提出者はこれらの結果を踏まえ、より直接的にフーリエ積分作用素の多重積を評価するすることにより(2)の評価を大幅に改善することに成功した。それによれば相関数に関する基本的な大きさの制限は幾何学的制約から当然予想される2階までの微分評価でよくなり、また、l1,l’1なども(簡単な式で書き表せる)より小さな整数にとれることがわかった。従来、多重積を計算するのには相関数の部分だけを先に抜き出して計算し、残りの振幅部分をいわゆる擬微分作用素の多重積として計算していたのであるが、そうすると各相関数に対して振幅が1である場合のフーリエ積分作用素の逆作用素を途中に使わなければならず、その分、全体としてのノルム評価が悪くなっていた。本論文提出者はいくつかの重要なアイデアでフーリエ積分作用素の多重積をより直接的に評価する方法を編み出し、上記の結果を得るに至った。同様のアイデアは既に藤原-熊ノ郷(直人)-谷口らによるシュレジンガー方程式の解の構成に見られるが今の問題に適用できるまでにはさらに大きな発展が必要であった。この意味で本論文提出者の業績は高く評価でき、今後この種の評価を伴う問題を解析する際の良き手本となると思われる。よって、論文提出者 熊ノ郷 直人は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/54599 |
 jと表象
jと表象 をもつRn上のFourier積分作用素を、I(
をもつRn上のFourier積分作用素を、I( jがすべて、十分恒等写像に近ければ、正準写像の合成
jがすべて、十分恒等写像に近ければ、正準写像の合成 をもつFourier積分作用素I(
をもつFourier積分作用素I(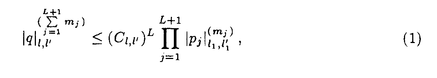
 は、
は、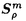 のsemi-normである。
のsemi-normである。 とする。
とする。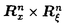 上のC∞-関数p(x,
上のC∞-関数p(x,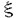 )が表象の族
)が表象の族 ,
, に対し、ある定数
に対し、ある定数 が存在し、
が存在し、
 とする。
とする。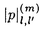 ,l,l’=0,1,2,...を、
,l,l’=0,1,2,...を、
 ).
). を正定数の増加列とし、t>0とする。
を正定数の増加列とし、t>0とする。 上の実数値C∞-関数
上の実数値C∞-関数 に属するとは、
に属するとは、

 をもつFourier積分作用素I(
をもつFourier積分作用素I(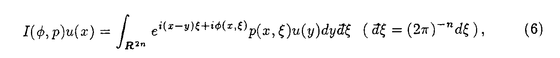
 *).
*). は正定数の増加列とし、j=1,2,…,L+1に対し、
は正定数の増加列とし、j=1,2,…,L+1に対し、 とする。
とする。 を仮定する。
を仮定する。
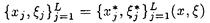 をもつ。
をもつ。 :
:
 =x,
=x, =
= 0とする。
0とする。 とおく。
とおく。 に対し、ある表象
に対し、ある表象 が存在し、
が存在し、

 とする。ここで、l1=n+1+l+l’,l’1=[2M+2
とする。ここで、l1=n+1+l+l’,l’1=[2M+2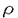 l+2(1+
l+2(1+ に注意してほしい。この論文の主定理では、この条件式の右辺のTは、T=min{1/(
に注意してほしい。この論文の主定理では、この条件式の右辺のTは、T=min{1/( ),1/(4n
),1/(4n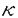 2)}であり、
2)}であり、 をどれだけ小さくとれば良いかは、次元nと相関数の2階までの微分だけで決めることができる。しかしながら、もとのH.Kumano-go-Taniguchiの証明では、表象1のFourier積分作用素の逆元が存在しなければならないため、この条件式の右辺のTは、
をどれだけ小さくとれば良いかは、次元nと相関数の2階までの微分だけで決めることができる。しかしながら、もとのH.Kumano-go-Taniguchiの証明では、表象1のFourier積分作用素の逆元が存在しなければならないため、この条件式の右辺のTは、 上の緩増加超関数f(x)に対して定義される特異積分作用素
上の緩増加超関数f(x)に対して定義される特異積分作用素