| 1Introduction (M,g)を、リーマン多様体とする。(M,g)上の閉2次形式Bを磁場とみなすと、M上の荷電粒子の運動方程式が次の様に定義される。  ここで、 :TM→TMは :TM→TMは  によって定まる交代作用素である。この運動方程式から、M上の力学系magnetic flow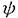 t:TM→TMが次の様に定義される。 t:TM→TMが次の様に定義される。  : : ここで、 は初期条件 は初期条件 (0)= (0)= ∈TMを満たす方程式(1)の解曲線である。B≡0、つまり ∈TMを満たす方程式(1)の解曲線である。B≡0、つまり ≡0の時はgeodesic flowになることに注意すると、magnetic flowはgeodesic flowの摂動であるといえる。この事実から、magnetic flowを幾何に応用する際に、geodesic flowによる幾何学の研究([3]等)が参考になると考えられる。実際、magnetic flowを使うと測地線の幾何の結果が一般化され、その過程で測地線の幾何では隠れていた概念が現れる。例えば、測地線上ではJacobi場の零点としての共役点とexponential mapの特異値としての共役点は同値なものであるが、磁場が存在するとこの同値関係は成立しない.そこで、これらを別々に扱うためにJacobi field conjugationとexponential map conjugationという概念を導入し、それぞれの概念に対応するを道具を作り出す必要が生じる。この様に、磁場が存在すると測地線の幾何では見えなかった構造が明らかになる。また、磁場Bが閉である必要性も見えてくる。magnetic flowはBが閉でなくても定義できるが、応用の際にはこの条件が重要な役割を果たす。では、以下で主な結果を述べる。 ≡0の時はgeodesic flowになることに注意すると、magnetic flowはgeodesic flowの摂動であるといえる。この事実から、magnetic flowを幾何に応用する際に、geodesic flowによる幾何学の研究([3]等)が参考になると考えられる。実際、magnetic flowを使うと測地線の幾何の結果が一般化され、その過程で測地線の幾何では隠れていた概念が現れる。例えば、測地線上ではJacobi場の零点としての共役点とexponential mapの特異値としての共役点は同値なものであるが、磁場が存在するとこの同値関係は成立しない.そこで、これらを別々に扱うためにJacobi field conjugationとexponential map conjugationという概念を導入し、それぞれの概念に対応するを道具を作り出す必要が生じる。この様に、磁場が存在すると測地線の幾何では見えなかった構造が明らかになる。また、磁場Bが閉である必要性も見えてくる。magnetic flowはBが閉でなくても定義できるが、応用の際にはこの条件が重要な役割を果たす。では、以下で主な結果を述べる。 2Magnetic flows of Anosov type コンパクト負曲率多様体上の接球面束UMに制限されたgeodesic flowはAnosov flowの例として知られている([2])。一般に、Anosov flowは構造安定性という性質を持つ。そこで、磁場が十分弱ければコンパクト負曲率多様体上のmagnetic flowもAnosov flowであると予想される。この予想に関しては、[1],[6]の結果が知られているが、これらを含む磁場Bに対する十分条件を最も理想的な形で求めることができた。定性的には次の様に書ける。 定義1 :TM→Mは標準射影であるとし、▽は(M,g)のLevi-Civita接続を表すとする。また、 :TM→Mは標準射影であるとし、▽は(M,g)のLevi-Civita接続を表すとする。また、 +によって +によって の転置作用素を表す。各々の の転置作用素を表す。各々の ∈TMに対して、 ∈TMに対して、 の自己準同型 の自己準同型 を次の様に定義する。 を次の様に定義する。  ここで、Rは曲率テンソルであり、(▽ )( )( ; ;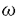 )は( )は(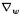 ) ) ( ( )を表す。 )を表す。 補題2全ての ∈TMに対して ∈TMに対して が対称作用素になるのは、Bが閉の時に限る。 が対称作用素になるのは、Bが閉の時に限る。 定理3(M,g)は磁場Bを持つコンパクトリーマン多様体とする。 は は における における の直交補空間への射影を表すとする。全ての の直交補空間への射影を表すとする。全ての ∈UMに対して ∈UMに対して が負定値ならば、Bによって定まるmagnetic flow が負定値ならば、Bによって定まるmagnetic flow 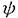 t:UM→UMはAnosov flowである。 t:UM→UMはAnosov flowである。 この結果を定量的に書くと次の様になる。 定理4(M,g)は磁場Bを持つコンパクトリーマン多様体とする。 max(M)は(M,g)の断面曲率の最大値を表すとする。Bが次の条件を満たせば、Bによって定まるmagnetic flow max(M)は(M,g)の断面曲率の最大値を表すとする。Bが次の条件を満たせば、Bによって定まるmagnetic flow 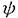 t:UM→UMはAnosov flowである。 t:UM→UMはAnosov flowである。  補題2から条件dB=0が本質的であることがわかる。 3The theorem of E.Hopf under magnetic fields E.Hopfはgeodesic flowを使って、共役点を持たないコンパクト曲面の全曲率は0以下で、等号が成り立つのは曲面が平坦のときに限ることを証明した([5])。更に、L.W.Greenはこの結果を一般次元の場合に拡張した([4])。magnetic flowを使うと、これらの結果を、磁場を持つコンパクトリーマン多様体の場合に一般化できる。ただし、この場合には、introductionで述べたようにJacobi field non-conjugationとexponential map non-conjugationの2つの概念が存在するので、それぞれに対してE.Hopfの定理が拡張される。特に興味深いのは、exponential map non-conjugationに対するものである. 定義5磁場Bの下でのexponential maps  :TM→Mはそれぞれ次の様に定義される。 :TM→Mはそれぞれ次の様に定義される。  ここで、 ( (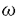 )≡ )≡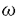 /g( /g(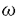 , ,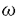 )1/2∈UMである。 )1/2∈UMである。 定義6d はそれぞれ はそれぞれ の微分を表すとする。 の微分を表すとする。 あるいは あるいは が退化する様な が退化する様な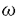 ∈TMが存在するならば、p= ∈TMが存在するならば、p= ( (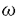 )と )と は は に沿ってBの下でexponential map conjugateであると呼ばれる。 に沿ってBの下でexponential map conjugateであると呼ばれる。 定理7(M,g)は磁場Bを持つコンパクトリーマン多様体とする。dVgはgによって定まるM上のリーマン測度を表すとする。方程式(1)の速度1の任意の解曲線上にBの下でのexponential map conjugate pointsが存在しなければ、次の幾何学的不等式が成り立つ。  ここで、S(p)はp∈Mにおけるスカラー曲率である。等号が成り立つのは、Bが一様で、(M,g)の普遍被覆多様体がユークリッド空間と正則断面曲率一定のケーラー計量を持つ開単位円達の直積である時に限る。正則断面曲率の値は 2の固有値に等しい。 2の固有値に等しい。 [1]T.Adachi,Kahler magnetic flows for a manifold of constant holomorphic sectional curvature,Tokyo J.Math.18(1995)473-483.[2]D.Anosov,Geodesic flows on compact Riemannian manifolds of negative curvature,Proc.Steklov Math.Inst.90(1967).[3]M.Berger,Lectures on geodesics in Riemannian geometry,Tata Inst. of Fund.Research,Bombay(1965).[4]L.W.Green,A theorem of E.Hopf,Michigan Math.J.5(1958)31-34.[5]E.Hopf,Closed surfaces without conjugate points,Pros.Nat.Acad.Sci.U.S.A.34(1948)47-51.[6]T.Sunada,Magnetic flows of a Riemannian surface,Proc.of KAIST Math.Workshop8,Analysis and Geometry,Korea(1993)93-108. |