| 内容要旨 | | ReshetikhinとTuraevは、向きの付いた閉3次元多様体Mの,量子SU(2)不変量 (M)を定義した。KirbyとMelvinは、この不変量が (M)を定義した。KirbyとMelvinは、この不変量が  3(M)と 3(M)と の積に分解されることを示した。ここで、 の積に分解されることを示した。ここで、 は3以上の素数であり、 は3以上の素数であり、 は量子SO(3)不変量と呼ばれている。Lickorish[3]はlinear skein theoryとTemperley-Lieb代数という概念を使って は量子SO(3)不変量と呼ばれている。Lickorish[3]はlinear skein theoryとTemperley-Lieb代数という概念を使って (M)を再定義した。 (M)を再定義した。 Seifertによれば、向きづけ可能な底空間を持つ、向きづけ可能なSeifert3次元多様体は次のパラメーターのシステムよって記述できる。 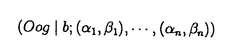 これらの記号の意味は本論文を参考にしてもらいたい。S2上のSeifert fibered有理ホモロジー球面を = = (Oo0|b;( (Oo0|b;(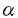 1, 1, 1),…,( 1),…,(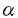 n, n, n))と表わす。HをH1(M;Z)の位数とし。 n))と表わす。HをH1(M;Z)の位数とし。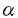 1,…, 1,…,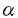 nを2以上の互いに素である整数とすると、 nを2以上の互いに素である整数とすると、 は次の関係式を満たす。 は次の関係式を満たす。 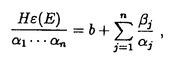 ここで (E)=E/|E|である。EはSeifert fibrationの有理Euler数E=b+ (E)=E/|E|である。EはSeifert fibrationの有理Euler数E=b+  j/ j/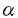 jである。 jである。 我々は、Lickorishの定義に基づいて、S2上のSeifert fibered有理ホモロジー球面の量子SO(3)不変量の公式を与える。量子SO(3)不変量は3次元多様体のblackboard framringから得られる。Singular fiberのsurgery表現をblackboard framingの表記法に変える際に連分数展開を行ったため、定義より得られる公式の の個数は多くなっている。多数の の個数は多くなっている。多数の を消すために、Gauss和やDedekind和などのいくつかの関係式を使った。pをある整数としたときに、 を消すために、Gauss和やDedekind和などのいくつかの関係式を使った。pをある整数としたときに、 はp はp ≡1(mod ≡1(mod  )を満たす整数である。E=H )を満たす整数である。E=H (E)/( (E)/(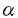 1… 1…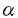 n)=b+ n)=b+ ( ( j/ j/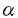 j)、 j)、 (E)=E/|E|、 (E)=E/|E|、 とする。s( とする。s( j, j,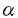 j)はDedekind和である。また、 j)はDedekind和である。また、 である。Uの元u=(u3,u4,…,un)に対して、|u|をその成分の和u3+u4+…+unとする。 である。Uの元u=(u3,u4,…,un)に対して、|u|をその成分の和u3+u4+…+unとする。 定理1[8] = = (Oo0|b;( (Oo0|b;(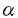 1, 1, 1),…,( 1),…,(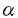 n, n, n))をS2上のSeifert fibered有理ホモロジー球面とする。 n))をS2上のSeifert fibered有理ホモロジー球面とする。 の量子SO(3)不変量は以下のようになる。 の量子SO(3)不変量は以下のようになる。 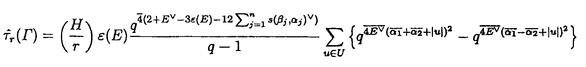 : : ここで、HはH1( ;Z)の位数、 ;Z)の位数、 は奇素数、( は奇素数、( )はLegendre符号、 )はLegendre符号、 である。 である。 他方、Cassonは、整数ホモロジー3次元球面のある不変量を提唱した。この不変量はCasson不変量と呼ばれている。Walkerは、Casson不変量の定義を、有理ホモロジー3次元球面にまで拡張した。この不変量はCasson-Walker不変量と呼ばれている。Seifert fibered整数ホモロジー球面のCasson不変量の公式は、福原氏、松本氏、坂本氏[1]とNeumann,Wahl[6]らによって与えられている。また、Lescop[2]はSeifet fibered有理ホモロジー球面のCasson-Walker不変量を計算した。村上斉氏[5]は、有理ホモロジー3次元球面Mと奇素数 に対して、 に対して、 は は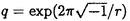 の整数係数多項式になることを示した。 の整数係数多項式になることを示した。 ∈Z[q]は以下のように整数係数のq-1にベキ級数展開できる。 ∈Z[q]は以下のように整数係数のq-1にベキ級数展開できる。  ただし、  が0であることに注意すると、0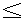 m m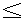  -2のとき( -2のとき( mod mod )∈Z/ )∈Z/ Zは、 Zは、 より決まるから、したがってMの位相不変量となる。大槻氏[7]は、Mの位相不変量の列 より決まるから、したがってMの位相不変量となる。大槻氏[7]は、Mの位相不変量の列 m(M),m=0,1,2,…が存在してmax(2m+2,H)より大きい任意の奇素数 m(M),m=0,1,2,…が存在してmax(2m+2,H)より大きい任意の奇素数 について について  m(M)と m(M)と は は を法にして合同であることを示した。{ を法にして合同であることを示した。{ m(M)}はOhtsuki不変量と呼ばれている。また、村上斉氏[5]は以下のことを示した。 m(M)}はOhtsuki不変量と呼ばれている。また、村上斉氏[5]は以下のことを示した。  ここで、 CW(M)はCasson-Walker不変量である。この結果は、定理1より、MがSeifert fibered有理ホモロジー球面 CW(M)はCasson-Walker不変量である。この結果は、定理1より、MがSeifert fibered有理ホモロジー球面 の場合にも成り立つ。また、計算の応用として、我々は2次のOhtsuki不変量の公式 の場合にも成り立つ。また、計算の応用として、我々は2次のOhtsuki不変量の公式 2( 2( )を求めた。 )を求めた。 定理 2 [8] = = (Oo0|b;( (Oo0|b;(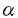 1, 1, 1),…,( 1),…,(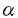 n, n, n))をS2上のSeifert fibered有理ホモロジー球面とする。 n))をS2上のSeifert fibered有理ホモロジー球面とする。 の2次のOhtsuki不変量は以下のようになる。 の2次のOhtsuki不変量は以下のようになる。 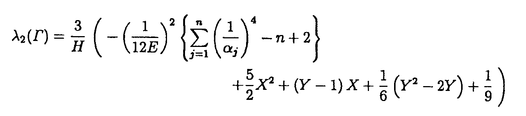 ここで、HはH1( ;Z)の位数を表し、E=H ;Z)の位数を表し、E=H (E)/( (E)/(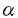 1… 1…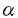 n)=b+ n)=b+ ( ( j/ j/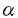 j)、 j)、 (E)=E/|E|である。XとYは次の関係式を満たす。 (E)=E/|E|である。XとYは次の関係式を満たす。  s(,)はDedekind和である。 公式は一見すると複雑な形をしているが、1次元ホモロジー群の位数、有理Euler数、特異ファイバー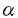 jとDedekind和の、これまで知られているいくつかの位相不変量の演算によって構成されている。LinとWang[4]は、整数ホモロジー3次元球面の2次のOhtsuki不変量 jとDedekind和の、これまで知られているいくつかの位相不変量の演算によって構成されている。LinとWang[4]は、整数ホモロジー3次元球面の2次のOhtsuki不変量 2が3の整数倍に成ることを示した。我々も、定理2より、整数ホモロジー3次元球面であるいくつかのBrieskorn多様体( 2が3の整数倍に成ることを示した。我々も、定理2より、整数ホモロジー3次元球面であるいくつかのBrieskorn多様体( (2,3,5), (2,3,5), (2,3,7), (2,3,7), (2,7,13), (2,7,13), (2,11,17), (2,11,17), (2,11,19), (2,11,19), (2,11,21), (2,11,21), (2,13,21), (2,13,21), (2,15,29), (2,15,29), (2,19,29), (2,19,29), (2,19,37), (2,19,37), (3,4,7), (3,4,7), (3,5,13), (3,5,13), (4,5,19), (4,5,19), (4,7,9), (4,7,9), (4,7,27))について (4,7,27))について 2( 2( )∈3Zを確かめた。その際、コンピューターの数式演算処理ソフトであるMathematicaを利用して計算をおこなった。またLinとWang[4]は、整数ホモロジー3次元球面のm次のOhtsuki不変量 )∈3Zを確かめた。その際、コンピューターの数式演算処理ソフトであるMathematicaを利用して計算をおこなった。またLinとWang[4]は、整数ホモロジー3次元球面のm次のOhtsuki不変量 mが6/m!の整数倍であることを予想した。我々も、mが1から10までのとき、いくつかのBrieskorn多様体( mが6/m!の整数倍であることを予想した。我々も、mが1から10までのとき、いくつかのBrieskorn多様体( (2,3,5), (2,3,5), (2,3,7), (2,3,7), (2,7,13), (2,7,13), (2,11,17), (2,11,17), (3,4,7))について (3,4,7))について m( m( )∈(6/m!)Zを導くことができた。 )∈(6/m!)Zを導くことができた。 参考文献[1]S.Fukuhara,Y.Matsumoto,K.Sakamoto:Casson’s invariant of Seifert homology 3-spheres,Math.Ann.287(1990),275-285.[2]C.Lescop:Invariant de Casson-Walker des spheres d’homologie rationnelle fibrees de Seifert,C.R.Acad.Sci.Paris,t.310 Serie I(1990),727-730.[3]W.B.R.Lickorish:The skein method for three-manifold invariants,J.Knot Theory and Its Ramifications No.2,2(1993),171-194.[4]X.-S.Lin,Z.Wang:On Ohtsuki’s invariants of integral homology 3-spheres,I,preprint.[5]H.Murakami:Quantum SO(3)-invariants dominate the SU(2)-invariant of Csaaon and Walker,to appear in Math.Proc.Cam.Phil.Soc.[6]W.D.Neumann,J.Wahl:Casson invariant of links of singularities,Comment.Math.Helvetici 65(1990),58-78.[7]T.Ohtsuki:A polynomial invariant of rational homology 3-spheres,to appear in Invent.Math.[8]C.Sato:Casson-Walker invariant of Seifert fibered rational homology spheres as quantum SO(3)-invariant,to appear in J.Knot Theory and Its Ramifications. |