{Xk;k 1}を独立同分布な確率変数列としてランダムウォーク{Sn;n 1}を独立同分布な確率変数列としてランダムウォーク{Sn;n 0}を次のように構成する。S0=0,Sn=X1+…+Xn,n 0}を次のように構成する。S0=0,Sn=X1+…+Xn,n 1.このランダムウォークに対して 1.このランダムウォークに対して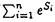 ,n ,n 1の形の確率変数を考える。この確率変数は一見特殊な形に見えるが実は確率過程の研究においてさまざまな場所で現れる。例えば、ランダムな差分方程式において、マルコフ過程のある状態への到達確率、分枝過程および出生死滅過程の生存確率やある世代の期待される生存者の総数などが挙げられる。 1の形の確率変数を考える。この確率変数は一見特殊な形に見えるが実は確率過程の研究においてさまざまな場所で現れる。例えば、ランダムな差分方程式において、マルコフ過程のある状態への到達確率、分枝過程および出生死滅過程の生存確率やある世代の期待される生存者の総数などが挙げられる。 Afanase’vはランダム媒質中を動くtransientなランダムウォークの最大値の末尾部分の確率の漸近挙動を調べる為に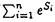 の形の確率変数のある汎関数の期待値を解析した。この問題を一般化しさらに彼の証明を明快なものにする為私は前の論文で彼の結果を含む形でランダムウォークの指数型汎関数の期待値の漸近挙動と共にある条件下での極限の正値性を調べた。そして、この結果をもともとの問題に適用する事によりAfanae’vの結果を若干ながら拡張することに成功した。しかし、私の論文では問題となったいる漸近極限の確率論的な表現は与えられなっかた。この様な漸近性を調べる問題では通常極限が正であることを言えば十分でありしかもランダムウォークの平均が0でない場合その極限を表現することは不可能なことが多いからである。 の形の確率変数のある汎関数の期待値を解析した。この問題を一般化しさらに彼の証明を明快なものにする為私は前の論文で彼の結果を含む形でランダムウォークの指数型汎関数の期待値の漸近挙動と共にある条件下での極限の正値性を調べた。そして、この結果をもともとの問題に適用する事によりAfanae’vの結果を若干ながら拡張することに成功した。しかし、私の論文では問題となったいる漸近極限の確率論的な表現は与えられなっかた。この様な漸近性を調べる問題では通常極限が正であることを言えば十分でありしかもランダムウォークの平均が0でない場合その極限を表現することは不可能なことが多いからである。 一方Afanase’vの問題の連続版である問題即ちドリフトをもつブラウン環境の中を移動する拡散過程の最大値の末尾部分の確率の漸近挙動が河津-田中両氏によって考えられた。一番困難な箇所の結果を得るにあたって彼らはYorによって得られたexp(Bt)と の同時分布に関する公式を使っている。そのYorの公式により彼らは次のことを示した。(彼らの証明を見ると彼らはこの様な一般的なかたちにはきずいていなかったようである。この形で示したのは筆者の修士論文であった。) の同時分布に関する公式を使っている。そのYorの公式により彼らは次のことを示した。(彼らの証明を見ると彼らはこの様な一般的なかたちにはきずいていなかったようである。この形で示したのは筆者の修士論文であった。) > > >0,としてf(x)=O( >0,としてf(x)=O( )とすると )とすると 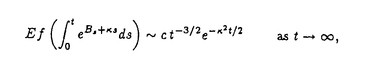 ここで 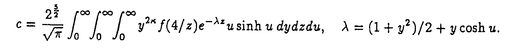 Afanase’vの問題の連続版であったにも関わらずその極限がcの様に明示される訳である。しかし、この極限cの確率論的ないみあいがどのようなものであるか知る為には非常にこみいったYorの公式の証明に立ち戻らなければならない。しかし、そうしたところでその確率論的な意味が得られるかどうかは難しいとおもわれる。最近上の漸近性に対して小谷氏は以下のの漸近性をYorの公式によらない方法で示した。  ここで、gやV 0はかなり広いクラスの関数でfは(0,∞)上の非負有界な測度 0はかなり広いクラスの関数でfは(0,∞)上の非負有界な測度 のラプラス変換とする。すなわち のラプラス変換とする。すなわち  ここで特にV(x)=ex,g(x)= とすることが可能でありCameron-Martin transfromとを併せて考えればfが上の形のときcは以下のように表される。 とすることが可能でありCameron-Martin transfromとを併せて考えればfが上の形のときcは以下のように表される。  ここでg (x,y)は全直線上の (x,y)は全直線上の のグリーン関数である。いいかればg のグリーン関数である。いいかればg (x,y)は (x,y)は を生成作用素にもつ拡散過程の(2exdxに関する)推移確率密度の時間パラメーターにかんするラプラス変換である。これでかなりはっきりした確率論的な表現がえられた訳である。この論文ではやはりfが上のような形を持つときの河津-田中両氏の結果のランダムウォーク版を考え、さらにcに相当する値を確率論的に表現する。これは筆者の前の論文ではえられなかった部分である。すこし詳しくいえばEX1>0でX1のmoment generating functionがある負の開区間で存在してfが(0,∞)上の非負有界な測度 を生成作用素にもつ拡散過程の(2exdxに関する)推移確率密度の時間パラメーターにかんするラプラス変換である。これでかなりはっきりした確率論的な表現がえられた訳である。この論文ではやはりfが上のような形を持つときの河津-田中両氏の結果のランダムウォーク版を考え、さらにcに相当する値を確率論的に表現する。これは筆者の前の論文ではえられなかった部分である。すこし詳しくいえばEX1>0でX1のmoment generating functionがある負の開区間で存在してfが(0,∞)上の非負有界な測度 のラプラス変換とすると のラプラス変換とすると 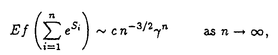 ここで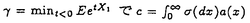 の形となる。a(x)は{Sn;n の形となる。a(x)は{Sn;n 0}のexcurtionが起こる時間とその高さから成るprocess(ascending ladder processと呼ばれる)とSnを平均0に変換したランダムウォーク(これはCameron-Martin formulaを使ってブラウン運動のドリフトを0にすることに相当する)のharmonic transformとで構成される。 0}のexcurtionが起こる時間とその高さから成るprocess(ascending ladder processと呼ばれる)とSnを平均0に変換したランダムウォーク(これはCameron-Martin formulaを使ってブラウン運動のドリフトを0にすることに相当する)のharmonic transformとで構成される。 この結果を得るにあたってランダムウォークに対する様々な条件付き極限定理を必要とした。特にSnが常に負の半区間にとどまるしたときの極限的な法則を調べた。このことはharmonic transformがそのように解釈されることを考えると自然な帰結とも言える。主要な補題のひとつとして次の結果を得た。ki1としてはしめのk次元分布(S1,…,Sk)末尾部のk次元分布(Sn,Sn-1,…,Sn-k-1)の同時分布を∧n=(S1 0,…,Sn 0,…,Sn 0)で条件付けてn→∞とするとこの分布は二つのk次元分布の積に弱収束する。すなわち漸近的に独立であり極限分布のひとつは先に述べたa(x)を構成するharmonic transform processの分布でありもうひとつは初期分布付きのharmonic transform processの分布である。この初期分布はSnの条件付き収束にともない現れるものである。ここで重要なことは末尾部k次元をSn,Sn-1,…,Sn-k-1と時間を逆にとることである。このように考えないと上の弱収束は得られないであろう。 0)で条件付けてn→∞とするとこの分布は二つのk次元分布の積に弱収束する。すなわち漸近的に独立であり極限分布のひとつは先に述べたa(x)を構成するharmonic transform processの分布でありもうひとつは初期分布付きのharmonic transform processの分布である。この初期分布はSnの条件付き収束にともない現れるものである。ここで重要なことは末尾部k次元をSn,Sn-1,…,Sn-k-1と時間を逆にとることである。このように考えないと上の弱収束は得られないであろう。 このような条件付き極限定理は古くはIglehart(1974)による(Sn|∧n)の収束がある。最近の結果としてはKeener(1992)による(S1,…,Sk|∧n)の収束が整数値のみを動くランダムウォークに対して、より一般の場合にはBertoin and Doney(1994)によって示された。我々の補題はその全ての結果を含みさらに拡張している。しかもその補題こそ定理の証明に必要なのである。 このほかに簡単だが重要な補題として本文中のLemma1とLemma9が挙げられる。Lemma1ではrenewal functionが最初のexcurtionがおこる位置の分布を決定するということをのべている。(x<0での結果)Lemma9はFubiniの定理の応用であるが初期分布をもつランダムウォークをtime reversalして考えるとき有効である。実際先に述べた主要な補題の証明に使われる。またside resultsとしてSection5の5)と7)がある。5)はよく知られているWiener-Hopf factorization identityの実軸上の類似でありある条件下ではWiener-Hopf factorization identityの形を保ったまま解析接続されることを示している。これは解析接続の理論では明かというわけでわない。ここでもLemma1と9が使われる。7)は先に述べた主要な補題の一次元ドリフト付きブラウン運動の類似であり三次元ベッセル過程が密接な関係にあることがわかる一つの例となっている。 |