| 内容要旨 | | キルヒホッフ方程式と呼ばれる次の準線型波動方程式 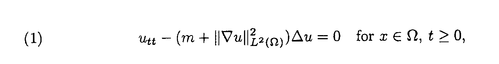 はKirchhoff(1883)により弦の非線形振動を記述する方程式として提唱された.ここで,mは非負の定数とする.他に弦の振動を記述する方程式としては,  が有名であるが,(2)は弦にかかる張力が弦の伸びによらず一定であるとの仮定の下で導出されるの対し,(1)は弦の伸長による張力の増大を反映させたモデルとなっている. (1)はBernstein(1940)の研究を発端にして可解性を中心に研究されてきた.近年,Yamazaki(preprint)などにより, = = ,m>0で,初期値が小さく無限遠方で減衰している場合,(1)の解は時間大域的に存在し,t→±∞で適当な波速の古典的な線型波動方程式の解に収束することが示された.またDickey(1980)は, ,m>0で,初期値が小さく無限遠方で減衰している場合,(1)の解は時間大域的に存在し,t→±∞で適当な波速の古典的な線型波動方程式の解に収束することが示された.またDickey(1980)は, が一次元有界区間の場合に,(1)の単一モードからなる解の安定性を研究している. が一次元有界区間の場合に,(1)の単一モードからなる解の安定性を研究している. 長時間の物理現象を観測する際には摩擦や粘性などエネルギーを散逸する効果が現れることが多い.我々は(1)に粘性項- utや摩擦項utを加えて得られる utや摩擦項utを加えて得られる 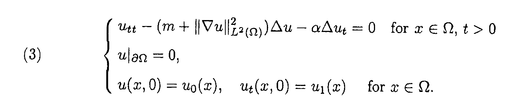 および 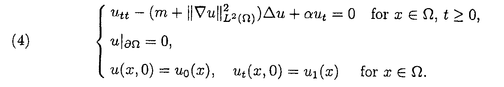 の解の長時間的挙動を解析した.ここで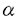 は正の定数, は正の定数, ⊂ ⊂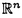 とする.(3),(4)の解のエネルギーは時間とともに単調に減少し,もし解が時間大域的に存在すればt→∞で(3),(4)の唯一の定常解である0に収束する. とする.(3),(4)の解のエネルギーは時間とともに単調に減少し,もし解が時間大域的に存在すればt→∞で(3),(4)の唯一の定常解である0に収束する. (3)の場合,粘性項の効果によりエネルギー解が時間大域的に存在する.また(4)は初期値のサイズが小さいことなどを仮定した場合,解が時間大域的に存在することが知られている. 定常解に収束する解の様子を調べるため,(3),(4)をu≡0の周りで線型化すると 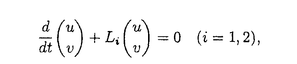 となる.ここで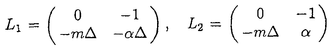 とする.いま, とする.いま, を を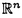 の有界領域とする.このとき,m>0の場合には,L1,L2のスペクトルは右半平面に含まれ,解の漸近展開の第一項は,線型化方程式の解で表される.しかしm=0の場合,L1,L2のスペクトルは0固有値と正の固有値からなるため,解のasymptoticsを求めるには,より高次の近似を行うことが必要になる.我々はm=0の場合に,t→∞における(3),(4)の解の挙動を記述する近似方程式を求めることを目標にした.以後m=0を仮定する場合,方程式(3),(4)を特に(3)0,(4)0と記すことにする. の有界領域とする.このとき,m>0の場合には,L1,L2のスペクトルは右半平面に含まれ,解の漸近展開の第一項は,線型化方程式の解で表される.しかしm=0の場合,L1,L2のスペクトルは0固有値と正の固有値からなるため,解のasymptoticsを求めるには,より高次の近似を行うことが必要になる.我々はm=0の場合に,t→∞における(3),(4)の解の挙動を記述する近似方程式を求めることを目標にした.以後m=0を仮定する場合,方程式(3),(4)を特に(3)0,(4)0と記すことにする. このような場合に,解の性質を解析する方法の一つとして無限次元力学系における中心多様体の理論がある.Part1では,Pego(1987)によって発見された変数変換を応用することで,(3)0を反応拡散方程式系に変換し,Chow-Lu(1988)の中心多様体の存在定理を適用した.中心多様体の理論を用いることで,(3)0は減衰する速さの異なる解ごとに,より単純な方程式に帰着させることができ,我々は以下の結果を得ることができた. ここで,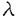 1< 1<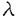 2< 2<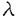 3<…をDirichlet0の境界条件の下での- 3<…をDirichlet0の境界条件の下での- の固有値のうち,値の相異なるものを小さい順に並べたものとし, の固有値のうち,値の相異なるものを小さい順に並べたものとし,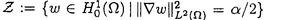 とする. とする. 定理1(本論Part1 Theorem A1). を を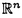 の有界領域とし,u(t)を(3)0の解とする.このとき, の有界領域とし,u(t)を(3)0の解とする.このとき,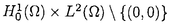 は以下の性質を満たす2つの集合A1,A2の直和に分解される. は以下の性質を満たす2つの集合A1,A2の直和に分解される. (i)A1は稠密な開集合,A2は内点をもたない閉集合である. (ii)(u0,u1)∈A1とする.このとき任意の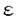 >0に対してt→∞で >0に対してt→∞で 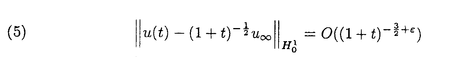 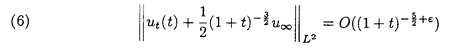 をみたすZの元u∞が存在する. (iii)(u0,u1)∈A2とする.このときk∈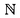 および および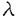 kに属する固有関数 kに属する固有関数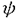 が存在し, が存在し,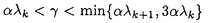 を満たす任意の を満たす任意の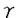 に対し に対し 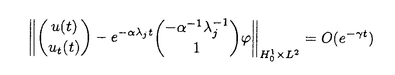 が成立する. 注意.(5),(6)は(3)0の解がt→∞で 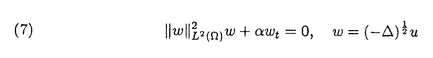 の解に収束することを主張している. 逆に,方程式(3)0は以下の性質をみたす. 定理2(本論Part1 Theorem A2). を有界領域とする.このとき,任意のu∞∈Zに対して,(5),(6)をみたす(3)0の解が存在する. を有界領域とする.このとき,任意のu∞∈Zに対して,(5),(6)をみたす(3)0の解が存在する. (3)0の解の減衰するオーダーは,Nishihara(1984,1993)などにより解析されていたが,中心多様体の理論を適用することで,t→∞での解の挙動を特徴づける近似方程式や解のasymptotic profileなどのより詳しい性質を明らかにすることができた.中心多様体の理論の偏微分方程式への応用例のほとんどは,中心多様体の次元が有限となる場合であるが,この問題は次元と余次元がともに無限大の例になっている. Part2では(4)0を解析した.(4)0のstrong solutionは以下の条件(H1),(H2)を満たす場合に解が時間大域的に存在することが知られている. 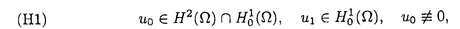 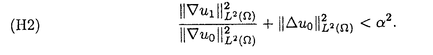 (4)0は,定常解が0のみであり,解のエネルギーが時間に関して単調に減少するという点は(3)0と同じである.初期値が有限個の固有関数で張られる場合,(4)0は有限次元の常微分方程式系に帰着するので,中心多様体の理論が適用できる.その結果,有限個の固有関数で張られる特別な場合には,ほとんどの解はt-1/2のオーダーで減少し 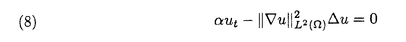 と同じasymptotic profileを持つこと,例外的に指数的に減衰する解が存在することがわかった.これらの性質は,より一般の初期値に対しても成立すると予想される.我々は,以下の結果を得た. 定理3(本論Part2 Theorem A).uを(4)0の解とし,初期値u0,u1が(H1),(H2)をみたすとする.このときk∈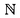 および および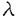 kに属する- kに属する- の固有関数 の固有関数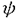 が存在し, が存在し,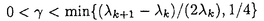 を満たす任意の を満たす任意の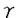 に対し に対し 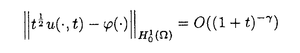 が成立する.ただし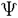 は は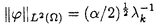 をみたすものとする. をみたすものとする. (H1),(H2)は,解が時間大域的に存在することを示すのに用いられている条件であり,定理3は,そのようなクラスに属するすべての解が(8)と同じasymptoticsをもつということを主張している.この結果は中心多様体の理論から予想される結果であるが,t→∞での近似方程式が常微分方程式ではなく放物型方程式であるなど,既成の中心多様体の理論の枠組みでは取り扱えない問題である. この問題で,解のdecay rateの上からの評価は標準的なエネルギー法の議論で得られる.しかし解のdecay rateの下からの評価は,単純な部分積分からは得られない.定理3を示す上では,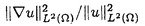 が適当な- が適当な- の固有値に多項式のオーダーで収束することを示すことが重要であった. の固有値に多項式のオーダーで収束することを示すことが重要であった. 参考論文では,方程式(4)0を = =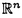 の場合に扱い,解のasymptoticsの第一項はやはり放物型方程式(8)の自己相似解で表されることを示した.全空間では- の場合に扱い,解のasymptoticsの第一項はやはり放物型方程式(8)の自己相似解で表されることを示した.全空間では- のスペクトルは0まで連続的にあることを反映し,仮定(H1),(H2)の下で解はt-1/2より遅い様々なオーダーで減衰することが示された.(参考論文Theorems2.2,2.3). のスペクトルは0まで連続的にあることを反映し,仮定(H1),(H2)の下で解はt-1/2より遅い様々なオーダーで減衰することが示された.(参考論文Theorems2.2,2.3). |
| 審査要旨 | | 論文提出者 水町徹は,弦の振動のモデルとしてよく知られるキルヒホッフ方程式を高次元に拡張した準線型波動方程式を考察し,これに摩擦や粘性項を付加した際に見られる解の減衰の様子を詳細に解明することに成功した. キルヒホッフ方程式と呼ばれる次の準線型波動方程式 はKirchhoff(1883)により弦の非線形振動を記述する方程式として提唱された方程式である.ここでmは非負の定数とする.弦の振動を記述する方程式としては,線形の波動方程式 が有名であるが,(2)は弦にかかる張力が弦の伸びによらず一定であるとの仮定の下で導出されるの対し,(1)は弦の伸長による張力の増大を反映させた,より精緻なモデルとなっている.論文提出者は(1)に粘性項- utや摩擦項utを加えて得られる以下のような2種類の方程式を考察した. utや摩擦項utを加えて得られる以下のような2種類の方程式を考察した. ここで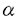 は正の定数, は正の定数, ⊂ ⊂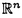 は有界領域である. は有界領域である. 方程式(3)については,エネルギー有限な初期値から出発した解は必ず時間大域的に存在することが知られている.いっぽう方程式(4)の場合は,時間大域解が常に存在するかどうかは不明であるが,初期値に実解析性やサイズの小ささなどを仮定すると解が時間大域的に存在することが知られている.ともあれ,いずれの方程式においても解のエネルギーは時間とともに単調に減少するので,時間大域的な解はすべてt→∞のとき0に減衰することが比較的容易に示される.しかしながら,減衰のオーダーをはじめ,減衰解の詳しい様子については,きわめて限られた結果しか得られていなかった. 論文提出者は,この方面の研究では過去に試みられたことのない斬新な手法を導入し,従来の結果を著しく改良することに成功した.その内容について,以下簡潔に説明する.なお,論文提出者はm=0およびm>0の両方の場合を扱っているが,以下では解析のより難しいm=0の場合に焦点を絞ることにする. 解の減衰の様子を調べるには,方程式をu≡0の周りで線型化して得られる作用素のスペクトルが重要な情報を与える.しかし方程式(3)および(4)の場合,線形化作用素のスペクトルは,多重度無限大の固有値0と安定固有値からなる.このような場合,解の減衰の様子を知るには1次近似に相当する線形化作用素の情報だけではまったく不十分であり,方程式の非線形性に本質的に根ざした解析が必要となる. 論文提出者は,方程式(3)に力学系の中心多様体の理論を適用することで,(3)の"ほとんどすべて"の解は多項式のオーダーで減衰し,t→∞のとき常微分方程式 の解と同じ漸近形をもつことを示すとともに.指数的に減少する例外的な解は熱方程式 と同じ漸近形をもつことを示した.解の漸近挙動についてのこのような詳しい解析は,無限次元力学系の視点を用いることで初めて可能になった.中心多様体の理論の偏微分方程式への応用例は,これまで全くなかったわけではないが,中心多様体の次元が有限となる場合に限られていた.これに対し,方程式(3)は,中心多様体の次元と余次元がともに無限大の例になっている. 論文提出者は,提出論文の後半で方程式(4)を考察し,強解が時間大域的に存在することが知られているクラスの初期値に対して,(4)の解の漸近形が の解と同じになることを示した.この結果は(3)に対して得られた結論と類似しているが,t→∞における近似方程式が常微分方程式ではなく放物型偏微分方程式である点などが異なっており,興味深い.この問題では,技術的理由から中心多様体の理論を直接適用することはできなかったものの,エネルギー法に無限次元力学系の視点を巧妙に組み合わせることで,解が特定の形状に近づきながら減衰することを証明した.(4)の解の漸近形を標準的なエネルギー法だけで求めることは困難であり,無限次元力学系の視点を用いたことで,計算が非常に見通しよく実行されている. これまでこの方面の研究においては,研究の手法は部分積分に基づくエネルギー法が主であったが,上記の研究結果は,無限次元力学系の理論がしばしば非常に強力な解析手段を提供しうること,また,たとえ無限次元力学系の理論が直接適用できない場合においても,指導原理として重要な役割を果たしうることを示唆している.この点において,論文提出者の仕事は,この方面の研究に新しい展開を与えたものとして高く評価できる. 以上の諸点を考慮した結果,論文提出者 水町 徹は,博士(数理科学)の学位を受けるにふさわしい十分な資格があると認める. |