| 内容要旨 | | この論文では区間置換写像(interval exchange transformation)の力学系を考察する.区間置換写像という概念は最初Keaneより導入された.この写像の性質は非常に興味深く,しかも他の力学系に多くの応用がある.例えば,閉曲面上の面積を保つ流れの研究,多角形のbilliard問題などである.与えられた一つの区間置換写像の性質については多くの研究がなされている.特筆すべきものとしてMasurとVeechによるKeane予想の解決がある.この論文では区間置換写像の全体IEを群と見て,その群の構造を考察した. 第1節では与えられた区間置換写像TがIEの中で無理数回転(irrational rotation)と共役かどうかの判定法をTの十分大きいiterationによる不連続点の個数を使って与えた.第2節はKatokとSataevの曲面上の面積を保つ流れの研究の復習である.第3節では可換な二つの区間置換写像T1,T2が与えられたときに,われわれは,あるコンパクト3次元多様体上の特異点を持つ余次元1のfoliationを構成した.このコンパクト3次元多様体はTi(i=1,2)から決まる二つのコンパクト曲面 iを含み,このfoliationを iを含み,このfoliationを iに制限したものは,ちょうど,区間置換Tiから定まるfoliationになっている.可換な二つの区間置換写像を与えることはトーラスの基本群からIEへの準同型を与えることと同値であることに注意すると,われわれは,このような準同型の幾何的実現を得たことになる. iに制限したものは,ちょうど,区間置換Tiから定まるfoliationになっている.可換な二つの区間置換写像を与えることはトーラスの基本群からIEへの準同型を与えることと同値であることに注意すると,われわれは,このような準同型の幾何的実現を得たことになる. 第1節. 区間置換写像というのは[0,1)あるいはS1上の方向を保つ,不連続点を高々有限個のみ持つような等長写像である.区間置換写像Tが無理数回転と共役であるとは,ある区間置換写像Sと無理数 が存在して,T= が存在して,T= S-1になることである.MasurとVeechの定理により,ほとんどすべての区間置換写像がuniquely ergodicである.しかし,実際に与えられた区間置換写像はuniquely ergodicであるかどうかという問題はそれほど簡単ではない.無理数回転は最も簡単なuniquely ergodicな例である.お互いに共役な区間置換写像は同じ力学系の性質を持っているので,与えられた区間置換写像が無理数回転と共役であるかどうかの判定方法が見つかれば面白いと思う.われわれが発見したのは,もしTの十分大きいiterationの不連続点の数が変わらないとすると,Tが無理数回転に共役であるという事実である.正確に述べるために,まずいくつかの記号を定義する.Tの不連続点を S-1になることである.MasurとVeechの定理により,ほとんどすべての区間置換写像がuniquely ergodicである.しかし,実際に与えられた区間置換写像はuniquely ergodicであるかどうかという問題はそれほど簡単ではない.無理数回転は最も簡単なuniquely ergodicな例である.お互いに共役な区間置換写像は同じ力学系の性質を持っているので,与えられた区間置換写像が無理数回転と共役であるかどうかの判定方法が見つかれば面白いと思う.われわれが発見したのは,もしTの十分大きいiterationの不連続点の数が変わらないとすると,Tが無理数回転に共役であるという事実である.正確に述べるために,まずいくつかの記号を定義する.Tの不連続点を 1,…, 1,…, m-1とし,d(T)をその数とする. m-1とし,d(T)をその数とする.  ∧(T)はD(T)の部分集合と見ることもある.(A,x,B)∈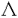 (T)のときにx∈ (T)のときにx∈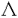 (T)と書く.xとBが1対1に対応するので,混乱は起こらない.次の定理は第1節の主定理である. (T)と書く.xとBが1対1に対応するので,混乱は起こらない.次の定理は第1節の主定理である. 定理1.3.m個の区間を持つ区間置換写像Tが無理数回転と共役であるための必要十分条件は次である:任意のn∈Nに対してTnが極小で,かつ自然数kと大きい自然数M(例えば より大きい)があって, より大きい)があって, を満たす.ただし, を満たす.ただし, . . 定理1.3を証明する前にまず次の定理を証明する. 定理1.4.区間置換写像Tが極小で,d(T)=d(T2),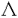 (T)∩ (T)∩ (T)= (T)= , ,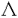 (T-1)∩ (T-1)∩ (T-1)= (T-1)= ならば,Tは無理数回転と共役である. ならば,Tは無理数回転と共役である. 定理1.4の証明は次の補題からでる. 定義1.5.(A,x,B)∈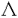 (T)とする.ただしA≠0,B≠1とする.xがremovableというのは次のいずれかを満たすときをいう. (T)とする.ただしA≠0,B≠1とする.xがremovableというのは次のいずれかを満たすときをいう. (1)A<B (2)A>B,かつC∈ (T)が存在して,A>C>B. (T)が存在して,A>C>B. 補題1.4.区間置換写像Tが極小かつd(T)=d(T2),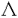 (T)∩ (T)∩ (T)= (T)= , ,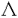 (T-1)∩ (T-1)∩ (T-1)= (T-1)= を満たすとする.x∈ を満たすとする.x∈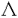 (T)がremovableならば,区間置換写像Sが存在して,d(STS-1)<d(T)であり,かつSTS-1も補題の条件を満たす. (T)がremovableならば,区間置換写像Sが存在して,d(STS-1)<d(T)であり,かつSTS-1も補題の条件を満たす. 第2節. 区間置換写像は曲面上の面積を保つ流れの研究と深い関連がある.流れがLebesgue測度を保つとき,曲面上にある閉じた曲線が存在して,それに対するPoincare写像は区間置換写像になる.逆に,ひとつの区間置換写像が与えられたとき,ある閉曲面およびその上の流れが作られて,ある曲線に対してのPoincare写像は元の区間置換写像と一致する.われわれは流れの回転集合(あるいはasymptotic cycle集合)に興味をもつ.トーラスの任意の連続の流れに対して,Franksはその流れの回転集合の次元は1に過ぎないことを証明した.しかも次元が1になる非自明な例も作った.種数がgの曲面に対して,Katokはその上の面積を保つ流れの回転集合はg次元に過ぎないことを証明した.Sataevによるその流れについての不変なergodic測度の数の評価を用いて,次のことは容易に分かる. 系2.1.任意のgに対して,種数gの曲面上位相推移的な面積を保つ流れが存在して,その流れの回転集合の次元はgである. 第3節. 第2節の議論からわかるように区間置換が与えられたとき,それを幾何的に実現すると曲面とその上の流れが作られる.このアイデアを一般化して,次のことが分かる.トーラスの基本群からIEへの準同型が与えられたときに,あるコンパクト3次元多様体と余次元1の特異点を持つfoliationがあって,そのfoliationのholonomy群は準同型の像と一致する.正確には, 定理3.1.T1,T2は区間置換写像でT1oT2=T2oT1を満たすとするとき,コンパクト3次元多様体Mと閉曲面 1, 1, 2かつ埋め込みi1: 2かつ埋め込みi1: 1→M,i2: 1→M,i2: 2→Mがあって,i1( 2→Mがあって,i1( 1)∩i2( 1)∩i2( 2)はS1になる.しかもM上の余次元1の特異点を持つfoliation 2)はS1になる.しかもM上の余次元1の特異点を持つfoliation があって, があって, はTjにより定まるfoliationである.j=1,2. はTjにより定まるfoliationである.j=1,2. 定理3.1に作られたfoliationの構造とその多様体の位相の関係を考えると,よく知られているPlanteの定理を使って次の定理が分かる. 定理3.3.(M, )は定理3.1のものとする.Lは )は定理3.1のものとする.Lは の中のleafとする.Lは多項式の増大度を持ち,その指数はmax{0,b1(M)-1}で抑えられる、ただし,b1(M)はMの第1betti数である. の中のleafとする.Lは多項式の増大度を持ち,その指数はmax{0,b1(M)-1}で抑えられる、ただし,b1(M)はMの第1betti数である. |
| 審査要旨 | | 区間置換写像は、重要な具体的な力学系として、その極小性、不変測度の個数などについて、多くの研究がなされ、ほとんどすべての区間置換写像は極小であり、ルベーグ測度をただ一つの不変測度として持つこと、極小ではあるが複数の不変測度を持つ区間置換写像は存在すること、などが知られていた。 本論文で、論文提出者は区間置換写像のなす群の構造についての研究を行っている。 無理数回転およびその区間置換写像による共役は、極小でありルベーグ測度をただ一つの不変測度として持つ簡単かつ重要な例である。論文提出者は本論文の第一部で、このような無理数回転に共役な区間置換写像の特徴付けに取り組み、区間置換写像の累乗の不連続点の個数により特徴付けた。 すなわち、Tが無理数回転と共役であることと任意の自然数nに対し、Tnが極小であり、ある自然数kとTの不連続点の個数と比べて十分大きな自然数Mに対し、Tk,T2k,…,TMkの不連続点の個数が一定であることは同値である。 これは、ほとんどすべての極小かつルベーグ測度をただ一つの不変測度として持つ区間置換写像は、無理数回転と共役ではないことを意味する重要な結果である。 本論文の第二部では、区間置換写像と曲面上の測度を保つ流れの対応について、知られている結果をまとめ、漸近サイクルの次元の評価とその評価が最良であることを考察した。 第一部の研究では区間置換写像のなす群を考えることが重要であった。区間置換写像のなす群の研究は始まったばかりであり、そのアーベル化の不変量として、分解合同不変量が知られているだけであった。第二部の区間置換写像の曲面上の流れとしての実現は、円周の基本群から区間置換写像のなす群への準同型の幾何的実現とみることができる。本論文の第三部では、さらに生成元を定めた曲面の基本群から区間置換写像のなす群への準同型を幾何的に3次元多様体上の横断的不変測度を持つ(ある種の特異点を許した)葉層構造として実現することができることを示した。さらに、この葉層の葉の成長度は多項式的であり、その次数を評価できることも示した。また、無理数回転と共役な可換な2つの区間置換写像の定める葉層を具体的に構成している。これらは3次元多様体論との関係において、今後の研究の基礎となるものであり、重要な構成である。 このように、本論文では多くの結果が得られており、これは1次元力学系理論に新しい知見を与え、寄与するところ大である。よって本論文提出者李思敏は博士(数理科学)の学位を授与されるに十分な資格があるものと認める。 |