数論幾何においてはベッチ、エタール、ド・ラーム、クリスタルなどの種々のコホモロジー理論が研究され、比較定理が証明されている。グロタンディークは、このことよりコホモロジー理論はモチヴィックであるという哲学をうちたてており、それは多くの数学者の信ずる事となっている。 この哲学は、ドリーニュにより、有理基本群(の副巾単商)もまたモチヴィックであるという哲学に拡張された。歴史的には、通常の有理基本群はクィレンによる考察がある。エタール基本群はグロタンディークにより定義された。また、ド・ラーム基本群はサリヴァンとシェンにより独立に構成された。サリヴァンは微分次数付代数の極小モデルを考えることにより、またシェンは反復積分を考えることにより、それを定義した。有理基本群上の混合ホッヂ構造はモーガンとハインにより構成された。そしてドリーニュは淡中圏とファイバー関手を用いた統一的な(ベッチ、エタール、ド・ラームの)有理基本群の構成を行い、種々の比較定理を示したのであった。 ドリーニュの哲学に従えば、標数p>0の体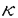 上の平滑な多様体Xに対しそのクリスタル基本群が定義され、Xが標数0の体上に平滑に持ち上がるとき、持ち上げのド・ラーム基本群との間に比較定理が成り立つべきである。しかし、ドリーニュは、標数0に持ち上がる多様体に対してのみクリスタル基本群を考えるに留まっており、またこの場合は、持ち上げのド・ラーム基本群にクリスタルフロベニウス写像を定義することによりクリスタル基本群を定義したのであった。クリスタル基本群は多様体Xが持ち上げをもたなくても定義されるべきものであり、また持ち上げに依らずに定義されるべきものであるから、彼の考察は最良のものとは言えない。 上の平滑な多様体Xに対しそのクリスタル基本群が定義され、Xが標数0の体上に平滑に持ち上がるとき、持ち上げのド・ラーム基本群との間に比較定理が成り立つべきである。しかし、ドリーニュは、標数0に持ち上がる多様体に対してのみクリスタル基本群を考えるに留まっており、またこの場合は、持ち上げのド・ラーム基本群にクリスタルフロベニウス写像を定義することによりクリスタル基本群を定義したのであった。クリスタル基本群は多様体Xが持ち上げをもたなくても定義されるべきものであり、また持ち上げに依らずに定義されるべきものであるから、彼の考察は最良のものとは言えない。 そこで、本論文では、クリスタル基本群の理論をドリーニュの哲学に従った方法により定義する。多様体のl進基本群の副巾単完備化を考えるときには、淡中圏として、「巾零な」(定義は本文を参照のこと)平滑 層の圏を考え、また、多様体のド・ラーム基本群を考える時は、淡中圏として、巾零で縁に沿って確定特異点型の可積分接続付連接層の圏を考える。では、クリスタル基本群を考える時は、どのような淡中圏を考えるべきであろうか?それはl進理論での平滑 層の圏を考え、また、多様体のド・ラーム基本群を考える時は、淡中圏として、巾零で縁に沿って確定特異点型の可積分接続付連接層の圏を考える。では、クリスタル基本群を考える時は、どのような淡中圏を考えるべきであろうか?それはl進理論での平滑 l層に対応するようなp進的なものの圏であるべきである。このような圏の候補はいくつか考えられる。対数的クリスタル景における巾零アイソクリスタルの圏、対数的収束景における巾零アイソクリスタルの圏、そして巾零過収束アイソクリスタルの圏である。我々は上の圏全てを考察し、クリスタル基本群を三通りの仕方で定義する。そして、それ等が矛盾なく定義されていることを示す。三つの定義にはそれぞれ利点があり、そのため我々はクリスタル基本群が満たすべき性質を証明することが出来る。また、我々はサリヴァンによる微分次数付代数の極小モデルの理論を用いて、クリスタル基本群の四つ目の定義を与える。これにより、クリスタル予想の基本群に対する類似を証明することが出来る。 l層に対応するようなp進的なものの圏であるべきである。このような圏の候補はいくつか考えられる。対数的クリスタル景における巾零アイソクリスタルの圏、対数的収束景における巾零アイソクリスタルの圏、そして巾零過収束アイソクリスタルの圏である。我々は上の圏全てを考察し、クリスタル基本群を三通りの仕方で定義する。そして、それ等が矛盾なく定義されていることを示す。三つの定義にはそれぞれ利点があり、そのため我々はクリスタル基本群が満たすべき性質を証明することが出来る。また、我々はサリヴァンによる微分次数付代数の極小モデルの理論を用いて、クリスタル基本群の四つ目の定義を与える。これにより、クリスタル予想の基本群に対する類似を証明することが出来る。 各部の内容を説明する。第一部(第1節及び第2節)は序文及び記法の説明である。第二部では本論文で用いられる圏論的事項を述べる。第3節ではテンソル圏及び淡中圏について復習する。またアーベルテンソル圏Cに対してその巾零部分NCを定義する。このNCは必ずしもアーベル圏にはならない。第4節ではこれがアーベル圏になるためのある充分条件を与える。これにより、後に考える種々の圏が淡中圏になることが確かめられる。 第三部では、加藤が定義した対数的クリスタル景における巾零アイソクリスタルの圏を用いてクリスタル基本群の第一の定義を与える。第5節では、対数的クリスタル景の定義や、その上のクリスタルの定義などの基本的事項を復習する。第6節ではクリスタル基本群の第一の定義を与える。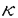 を標数p>0の完全体とし、良い対数的概型の固有、平滑、整な射(X,M)→(Spec を標数p>0の完全体とし、良い対数的概型の固有、平滑、整な射(X,M)→(Spec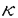 ,N)である種の条件を満たすもの及び良い対数的形式概型(SpfW,N)への完全閉埋入射(Spec ,N)である種の条件を満たすもの及び良い対数的形式概型(SpfW,N)への完全閉埋入射(Spec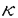 ,N)→(SpfW,N)が与えられたとする。但し、Wは ,N)→(SpfW,N)が与えられたとする。但し、Wは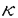 のヴィット環とする。 のヴィット環とする。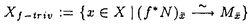 の の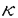 有理点xに対して、(X,M)の(SpfW,N)上のxを基点とするクリスタル基本群 有理点xに対して、(X,M)の(SpfW,N)上のxを基点とするクリスタル基本群 ((X,M)/(SpfW,N),x)を対数的クリスタル景((X,M)/(W,N))crys上の巾零アイソクリスタルの圏を用いて定義する。この群はWの分数体上の副巾単代数群の構造をもつ。定義より、標準的同型 ((X,M)/(SpfW,N),x)を対数的クリスタル景((X,M)/(W,N))crys上の巾零アイソクリスタルの圏を用いて定義する。この群はWの分数体上の副巾単代数群の構造をもつ。定義より、標準的同型  があることがわかる。但し、右辺の は加藤の定義した対数的クリスタルコホモロジーである。更に良い条件の下で、クリスタルフロベニウスと呼ばれるフロベニウス線形な自己準同型の存在と、それが自己同型であることが示される。 は加藤の定義した対数的クリスタルコホモロジーである。更に良い条件の下で、クリスタルフロベニウスと呼ばれるフロベニウス線形な自己準同型の存在と、それが自己同型であることが示される。 第四部では、対数的収束景上のアイソクリスタルの圏を用いて、クリスタル基本群の第二の定義を与える。第7節では、対数的概型に対し収束景を定義し、クリスタル基本群の第二の定義を与える。Vを剰余体が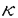 となるような混標数の完備離散付置環とし、Kをその分数体とする。そして上のような(X,M)→(Spec となるような混標数の完備離散付置環とし、Kをその分数体とする。そして上のような(X,M)→(Spec ,N)と、良い対数的形式概型(SpfV,N)への完全閉埋入射(Spec ,N)と、良い対数的形式概型(SpfV,N)への完全閉埋入射(Spec ,N)→(SpfV,N)が与えられたとする。このとき、Xf-trivの ,N)→(SpfV,N)が与えられたとする。このとき、Xf-trivの 有理点xに対して、(X,M)の(SpfV,N)上のxを基点とするクリスタル基本群 有理点xに対して、(X,M)の(SpfV,N)上のxを基点とするクリスタル基本群 ((X,M)/(SpfV,N),x)を対数的収束景((X,M)/(V,N))conv上の巾零アイソクリスタルの圏を用いて定義する。この群はK上の副巾単代数群の構造をもつ。第8節では、ド・ラーム基本群との比較定理を証明する。つまり、(X,M)が(SpecV,N)上固有、平滑、整な概型に持ち上がる時にクリスタル基本群 ((X,M)/(SpfV,N),x)を対数的収束景((X,M)/(V,N))conv上の巾零アイソクリスタルの圏を用いて定義する。この群はK上の副巾単代数群の構造をもつ。第8節では、ド・ラーム基本群との比較定理を証明する。つまり、(X,M)が(SpecV,N)上固有、平滑、整な概型に持ち上がる時にクリスタル基本群 ((X,M)/(SpfV,N),x)が持ち上げの一般ファイバーのド・ラーム基本群と同型であることを示す。第9節では、V=Wの時に、二つのクリスタル基本群の定義が一致することを示す。 ((X,M)/(SpfV,N),x)が持ち上げの一般ファイバーのド・ラーム基本群と同型であることを示す。第9節では、V=Wの時に、二つのクリスタル基本群の定義が一致することを示す。 第五部では、クリスタル基本群の第三の定義を与える。第10節では、リジッド解析幾何の基本事項を復習して、クリスタル基本群の第三の定義を与える。 ,V,Kを上の通りとする。 ,V,Kを上の通りとする。 上平滑な多様体XとXの 上平滑な多様体XとXの 有理点xに対して、XのSpfV上の、xを基点とするクリスタル基本群 有理点xに対して、XのSpfV上の、xを基点とするクリスタル基本群 (X/SpfV,x)を、XのV上の巾零過収束アイソクリスタルの圏を用いて定義する。第11節では、クリスタル基本群の第二の定義と第三の定義が次の意味で矛盾なく定義されていることを示す。即ち、(X,M)をXが (X/SpfV,x)を、XのV上の巾零過収束アイソクリスタルの圏を用いて定義する。第11節では、クリスタル基本群の第二の定義と第三の定義が次の意味で矛盾なく定義されていることを示す。即ち、(X,M)をXが 上固有であるような対数的正則な対数的概型とし、 上固有であるような対数的正則な対数的概型とし、 とおく。この時、Uの とおく。この時、Uの 有理点xに対して第二の定義によるクリスタル基本群 有理点xに対して第二の定義によるクリスタル基本群 ((X,M)/SpfV,x)が第三の定義によるクリスタル基本群 ((X,M)/SpfV,x)が第三の定義によるクリスタル基本群 (U/SpfV,x)に標準的に同型になることを示す。 (U/SpfV,x)に標準的に同型になることを示す。 第六部では、サリヴァンの微分次数付代数の極小モデルの理論を用いてクリスタル基本群の第四の定義を与える。第12節では、微分次数付代数についての基本事項を復習して、ド・ラーム=ヴィット複体を用いて、クリスタル基本群の第四の定義を与える。ここでは、第一の定義において、対数的構造Nが自明な時のみを考える。第13節では、クリスタル基本群の第一の定義と第四の定義が一致することをシンプソンによる微分次数付圏の理論を用いて示す。第14節では、p進ホッヂ理論において重要なクリスタル予想(フォンテーヌとメッシングにより部分的に、そしてファルティングスにより完全に解決された)の、基本群に対する類似を、この第四の定義を利用して証明する。証明のポイントは、多様体が固有なときには、基本群がコホモロジー環の第一極小モデルで書けることで、これにより、通常の(コホモロジーに対する)クリスタル予想に帰着できる。 第七部(第15節)では、接空間的基点及び接空間的写像の理論を、クリスタル基本群(ここでは第二の定義を用いる)に対して構成する。これも、クリスタル以外の基本群に対しては、ドリーニュが構成しているものである。クリスタル基本群の場合、この理論の構成には対数的構造が重要な役割を果たす。 |