この論文の目的は、CassonとWalkerによって定義された(整係数)ホモロジー3球面(整係数のホモロジー群がS³のそれに一致する3次元多様体)の中の結び目に対する不変量と、その結び目に沿ったホモロジー球面の0/1Dehn手術のFloerホモロジー群との関係を明らかにすることである。

　周知のように、任意の3次元多様体はS³のフレーム付きリンクに沿ったDehn手術により得られる。従って、3次元多様体の位相不変量の計算には、Dehn手術に対する振る舞いが決定的に重要である。ホモロジー球面の位相不変量としては、Casson不変量とFloerホモロジー群が知られている。

　ホモロジー球面のCasson不変量のDehn手術に対する振る舞いは、いわゆるCassonの結び目不変量を用いて記述されることが知られている。ホモロジー球面に対するCasson不変量の場合と違い、結び目不変量の定式化には結び目に付随したHeegard分解M＝W₁W₂をとる必要がある(ここでW₁とW₂は互いに同相なハンドル体、は2つのハンドル体の共通の境界となる曲面で結び目をBounding simple closed curveとしてもつもの)。一方、ホモロジー球面のFloerホモロジー群のDehn手術に対する振る舞いは、Floerの三角形とよばれる完全系列により記述されることが知られている。具体的には、Mをホモロジー球面、KをM内の結び目、M’,M"をそれぞれMのKに沿った1/0,0/1Dehn手術として、次のように書ける(M’はホモロジー球面、M"はホモロジーS¹×S²になる)。まずCasson不変量については、をホモロジー球面のCasson不変量、’を結び目のCasson不変量として、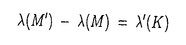

　がなたつ。Floerホモロジーについては、Dehn手術から標準的にきまる同境によって誘導される系列

　が完全系列になる。これがFloerの三角形とよばれるものである。

　いずれの結果についても、多様体にはホモロジー球面という制限がつくが、Casson不変量に対する結果はWalkerにより、有理ホモロジー球面(有理係数のホモロジー群がS³のそれに一致する3次元多様体)に対するDehn手術公式に一般化されている。この論文の結果は、Floerの三角形の有理ホモロジー球面への一般化、及びそのFloerホモロジーの具体的な計算への応用の第一歩を与えるものである。

　ホモロジー球面のCasson不変量とFloerホモロジー群の間には、つぎのような関係

　のある事がTaubesにより示されている。ここで右辺はMのFloerホモロジー、HF_*(M)のEuler数と見るべき量で、M上のSU(2)束の接続全体のなす無限次元空間を使い、Atiyah-Hitchin-Singer複体の指数を計算して得られる。一方、左辺は₁()のSU(2)表現全体のなす有限次元空間を使い、交点数の計算をして得られる。

　この論文ではTaubesの方法を変形して、結び目のCasson不変量の場合に適用する。結果を定理の形に書くと、

　金子真隆の論文「Casson’s knot invariant and Gauge theory」は、3次元多様体のゲージ理論を用いて得られる不変量に関するものである。

　1985年キャッソンはホモロジー3球面Mの重要な不変量を発見したが、それは基本群のSU(2)への表現の「符号付きで数えた」個数である。タウベスは1990年このキャッソンの不変量がM×R上のゲージ理論を用いて再構成できることを証明した。このタウベスの仕事は、フレアーによる3次元多様体のフレアーホモロジーの発見にいたる中心的なステップをなしている。(フレアーホモロジーのオイラー数の半分がキャッソンの不変量である。)

　キャッソンは彼の発見した不変量を計算する方法を同時に与えているが、それは、結び目についてのデーン手術で不変量がどう変わるかを決定したことに基づいている。ここで登場するのがキャッソンの結び目不変量である。

　フレアーは、結び目についてのデーン手術でフレアーホモロジーがどう変わるかを記述する完全系列を示している。この完全系列を用いると、キャッソンの結び目不変量は、その結び目に沿ってホモロジー3球面をデーン手術して得られる(S²×S¹と同じホモロジーを持つ)多様体のフレアーホモロジーのオイラー数であることがわかる。

　フレアーの完全系列は、結び目がホモロジ-3球面である場合にだけ証明されていて、より一般の3次元多様体に対してそれに当たるものが何かはよく分かっていない。深谷等によれば、おそらく、全く同じ完全系列は成り立たないだろうと言われている。

　一方で、キャッソンの不変量はウォーカーによって、有理ホモロジー球面に対して一般化され、デーン手術との関係も明らかになった。他方は、深谷等によってフレアーホモロジーはより一般の3次元多様体にも(いろいろなやり方で)一般化されている。

　従って、フレアーの完全系列をより一般の3次元多様体に対して、証明しようとしたとき、どのような理由でどのような場合に破綻が起こるかを知ることは3次元多様体のゲージ理論の中心的な問題の一つである。

　金子真隆の論文はこの問題にアタックするための最初の手がかりを与えるものである。

　金子は、まずキャッソンの結び目不変量とホモロジーS²×S¹のフレアーホモロジーに対する上記の事実の、フレアーの完全系列によらない証明を与えた。フレアーの完全系列は非線形偏微分方程式に基づいて証明されているのに対して、金子の証明は線形偏微分方程式の族の指数を用いて成されており、より簡明である。また、この証明は、上記のタウベスによるキャッソンの不変量のM×R上のゲージ理論を用いた再構成の自然な一般化である。

　次に、金子はこの結果をウォーカーの有理ホモロジー球面の中の結び目の不変量とホモロジーS²×S¹のフレアーホモロジーに対するものに一般化した。金子は結び目の表すホモロジー類が0であると仮定している。(この仮定がないと結果そのものが成り立たないと考えられる。)この結果は、例えば、フレアーの完全系列の類似がホモロジー類が0である結び目までは成り立つのではないかということを強く示唆しているように思われる。

　このように金子の結果はデーン手術とフレアーホモロジーの関係を研究する確実な第一歩を与えるもので、より進んだ重要な研究への出発点を与えるものである。

　金子の研究している問題は、ドナルドソン、フレアーを含む、多くの著名なゲージ理論の研究者が、研究していた問題である。サイバーグ・ウィッテン理論の副産物としてモノポール方程式が4次元トポロジーにもたらされて以来、ヤンミルズ理論に基づくゲージ理論を研究している研究者はあまり多くない。しかし、特に3次元ゲージ理論についてはヤンミルズ理論に基づくフレアーホモロジーは(サイバーグ・ウィッテン理論に比べて)平坦接続との関係が自然につくなど、明白な利点を持っている。従って、流行にとらわれず重要な問題を研究し、着実な一歩を与えた金子の研究は高く評価される。

　よって本論文提出者金子真隆は博士(数理科学)の学位を授与されるに十分な資格があるものと認める。