| 内容要旨 | | リーマン面からコンパクトリー群への調和写像全体のなす空間へのループ群の作用が、M.A.GuestとY.Ohnitaにより定義された。のちに、J.Dorfmeister,F.Pedit,H.Wuらにより、リーマン面からコンパクト対称空間への調和写像全体のなす空間へのループ群の作用の存在が示された。さらにこれは、F.E.BurstallとF.Peditにより、リーマン面からk-対称空間への特別な調和写像のクラスすなわち原始的調和写像全体へのループ群の作用に一般化された。k-対称空間とは、リー群Gの位数kの自己同型 の固定点集合HでGを割った等質空間G/Hである。k=2のときが対称空間である。この論文では、リーマン面から簡約可能な等質空間への特別な調和写像のクラスを定義し、それら全体のなす空間へのループ群の作用の存在を示す。 の固定点集合HでGを割った等質空間G/Hである。k=2のときが対称空間である。この論文では、リーマン面から簡約可能な等質空間への特別な調和写像のクラスを定義し、それら全体のなす空間へのループ群の作用の存在を示す。 リーマン多様体からリーマン多様体への調和写像の一般化として、リーマン多様体(M,h)からアファイン多様体(N,▽)への滑らかな写像 に対して、アファイン調和写像を に対して、アファイン調和写像を  により定義することができる。ただしここで{ei}i=1,…,nは、リーマン多様体Mの接バンドルTMの局所的な正規直交フレームで、上の定義は正規直交フレームのとり方によらない。特別な場合として、リーマン面からアファイン多様体(N,▽)への滑らかな写像 に対して、 に対して、  により、▽-調和写像を定義することができる。ただしここで(z)はリーマン面の等温座標で、上の定義は座標のとり方によらない。この論文では、とくに像空間が簡約可能な等質空間G/Hのときを考え、アファイン接続は、リー群Gのリー環gの簡約可能な分解  により、自然に定まる標準的接続▽Canを考える。これはK.Nomizuの意味での第二種標準的接続に他ならない。▽Can-調和写像は、g上のAd(G)-不変な正定値2次形式から誘導されるG/Hの不変リーマン計量に関して調和写像であることがわかる。 ここで、特別な▽Can-調和写像である -写像を次のようにして定義する。まず -写像を次のようにして定義する。まず :G→Gをコンパクトリー群Gの自己同型とし、Hを :G→Gをコンパクトリー群Gの自己同型とし、Hを の固定点集合とする。さらにgをGのリー環、hをHのリー環とする。リー群の自己同型 の固定点集合とする。さらにgをGのリー環、hをHのリー環とする。リー群の自己同型 の微分を原点において考えると、リー環gの自己同型が得られるが、これも同じ記号 の微分を原点において考えると、リー環gの自己同型が得られるが、これも同じ記号 でかくことにする。すると でかくことにする。すると の固有値 の固有値 によりリー環gの複素化gCの直和分解 によりリー環gの複素化gCの直和分解  が得られる。ただしここで は固有値 は固有値 の固有空間である。このとき の固有空間である。このとき 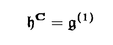 であり、  とおくことにより、簡約可能な分解  が得られる。すなわち簡約可能な等質空間G/Hが得られる。可縮なリーマン面 からG/Hへの滑らかな写像 からG/Hへの滑らかな写像 に対し、ファイブレーション に対し、ファイブレーション  への持ち上げF、すなわちF: →Gなる写像で、 →Gなる写像で、  となるものを のフレーミングという。ここで のフレーミングという。ここで のフレーミングFに対し、 のフレーミングFに対し、  とおくと、 は は 上のg-値1-形式となる。 上のg-値1-形式となる。 をリー環gの分解 をリー環gの分解  に従って、  と分解し、さらにリーマン面 の複素構造により、 の複素構造により、 mを mを  と分解する。ここで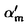 は(1,0)-形式、 は(1,0)-形式、 は(0,1)-形式である。 は(0,1)-形式である。 2が 2が -値となるとき -値となるとき を を -写像という。この定義はフレーミングFのとり方によらない。 -写像という。この定義はフレーミングFのとり方によらない。 -写像は▽Can-調和写像であることがわかる。 -写像は▽Can-調和写像であることがわかる。 リーマン面 上の1-形式 上の1-形式 は、可積分条件であるMaurer-Cartanの方程式 は、可積分条件であるMaurer-Cartanの方程式 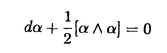 を満たすが、各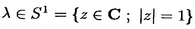 に対して、 に対して、  とおくと、 が が -写像であることより、 -写像であることより、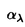 は各 は各 ごとに ごとに  をみたす。従って各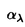 は積分できて、 は積分できて、 となる写像 となる写像  が存在する。このような を拡張フレーミングという。逆にこのような拡張フレーミングがあると、F1を自然射影 を拡張フレーミングという。逆にこのような拡張フレーミングがあると、F1を自然射影 :G→G/Hで下におとすことにより、 :G→G/Hで下におとすことにより、 oF1: oF1: →G/Hは →G/Hは -写像となる。 -写像となる。 -写像に対して、フレーミングののとり方に自由度があることを考慮すると、基点p0∈ -写像に対して、フレーミングののとり方に自由度があることを考慮すると、基点p0∈ を固定する を固定する -写像全体の空間 -写像全体の空間  は、  とおくとき、  と同一視される。 そこで拡張フレーミングの空間 にループ群を次のようにして作用させる。まず始めにループ群 にループ群を次のようにして作用させる。まず始めにループ群 を を  により定義する。ただしここで、0< <1を固定し、半径 <1を固定し、半径 の円周を の円周を ,半径1/ ,半径1/ の円周を の円周を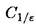 とするとき、 とするとき、  である。さらにループ群 の適当な部分群 の適当な部分群 , , を定めると、ループ群 を定めると、ループ群 の元gは、 の元gは、 の元gEと の元gEと の元gIの積 の元gIの積  と一意的に分解されることがわかる。拡張フレーミング はパラメータ はパラメータ をループパラメータとみなすことにより、リーマン面 をループパラメータとみなすことにより、リーマン面 からループ群 からループ群 への写像 への写像 と思えるが、 と思えるが、 ∋gに対し、 ∋gに対し、 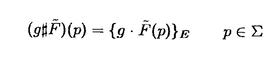 とおくと は再び拡張フレーミングとなることがわかる。ただしここで{ は再び拡張フレーミングとなることがわかる。ただしここで{ }Eとは、ループ群の元 }Eとは、ループ群の元 を上のように2つの部分群の積に分解したときの前者の部分である。このようにして、ループ群 を上のように2つの部分群の積に分解したときの前者の部分である。このようにして、ループ群 が拡張フレーミングの空間 が拡張フレーミングの空間 に作用することがわかったが、この作用は に作用することがわかったが、この作用は / / への作用を誘導することもわかる。従ってループ群 への作用を誘導することもわかる。従ってループ群 を を -写像の空間 -写像の空間 に作用させることができる。 に作用させることができる。 |
| 審査要旨 | | 近年リーマン多様体の間の調和写像(harmonic map)の研究が活発にされており大きな成果を納めている.この調和写像の重要な例としてはリーマン幾何学で基本的な測地線,極小曲面あるいは調和関数がある. リーマン多様体(M,h),(N,g)が与えられたとする.MからNへの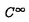 写像の全体を 写像の全体を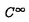 (M,N)で表す.汎関数を (M,N)で表す.汎関数を で定義する.fがこの汎関数Eの危点(critical point)であるとき(M,h)から(N,g)への調和写像と呼ぶ.(N,g)のLevi-Civita接続を▽gで表すときfが調和写像であるための必要十分条件はfが2階の準線形楕円型偏微分方程式系 を満たすことである(ただし,e1,...,emは正規直交基底である). さて調和写像の特別な例である調和関数,測地線の場合上記方程式はそれぞれラプラシアン,常微分方程式系となるので微分方程式の立場からそれぞれ調和積分論,モース理論として非常に詳しく研究がなされている.Mの次元が2次元のときの調和写像を便宜上調和曲面と呼ぶことにする.これは古典的極小曲面論に重要な手段を提供することから1970年以来非常に多くの興味ある研究がなされてきた.とくに(N,g)がコンパクト対称空間の場合には可積分系理論からの手法が使えることが最近になって発見され研究の一層の推進をもたらしている. 論文提出者が博士論文のテーマとして選んだのは調和曲面論で上記の研究環境のもとに研究を進めてきた.出発点は上記の方程式(1)をよく考察すると(N,g)はリーマン多様体である必要はなく,アフィン多様(N,▽)であれば意味があるということである.リーマン面(M,h)とアフィン多様(N,▽)が与えられたときf∈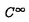 (M,N)が方程式系 (M,N)が方程式系 を満たすとき(M,h)からアフィン多様(N,▽)へのアフィン調和曲面と呼ぶ.論文提出者は学位論文で上述した(N,g)がコンパクト対称空間の場合に可積分系理論の手法で得られた調和曲面の諸結果を,(N,g)がもっと一般的にアフィン多様(G/K,▽can)にして拡張できることを明らかにした.ただしここでG/K簡約可能な等質空間で▽canはその上のK.Nomizuの意味で第2種標準的不変アフィン接続である.もう少し詳しく述べまよう.g, をリー群G,Kのリー環として をリー群G,Kのリー環として をG/Kに付随した簡約可能な分解とする.さて任意のf∈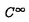 (M,G/K)に対してファイブレーション (M,G/K)に対してファイブレーション への持ち上げ があるとする.さらにgに値をもつ一次微分形式 f=F-1dFを考える.上記(2)の分解に従ってと分解し,さらにリーマン面(M,h)の複素構造により f=F-1dFを考える.上記(2)の分解に従ってと分解し,さらにリーマン面(M,h)の複素構造により m= m= (1,0)m+ (1,0)m+ (0,1)mと(1,0)-形式,(0,1)-形式に分解する.さてGのループ群 (0,1)mと(1,0)-形式,(0,1)-形式に分解する.さてGのループ群 (G)のリー環を (G)のリー環を (g)で表す.ここで (g)で表す.ここで (g)の元 (g)の元 を を で定義する.申請者が発見したことはfがアファイン調和曲面であるための必要十分条件は大まかに言って なる完全積分条件を満たすことである.もし(3)が成り立てばよく知られた事実によりループ群 (G)の元が存在してとなる.以上によりアフィン調和曲面に対応してループ群 (G)の元が存在してとなる.以上によりアフィン調和曲面に対応してループ群 (G)の元が存在してがなりたつことになる.さらに論部提出者は{アフィン調和曲面}で生成されるループ群 (G)の元が存在してがなりたつことになる.さらに論部提出者は{アフィン調和曲面}で生成されるループ群 (G)の部分群を大まかに言って決定した. (G)の部分群を大まかに言って決定した. 論文提出者の博士論文は現在活発に研究がなされている調和写像の分野に新しい知見を与えるものである.よって,論文提出者檜垣優徳は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. |