Lozi familyとは

　で与えられる二次元平面上の区分的線形同相写像の族である。ここで、a、bは実パラメータで、b≠0とする。この族は、Lorenz方程式のPoincare断面の単純化として得られたHenon familyが持つ性質(安定、不安定多様体の大域的配置、分岐現象など)の幾つかを共有していると考えられている。実際この族に対しても、適当なパラメータの選び方に対してstrange attractorの存在がMisiurewiczによって示されているなど、その表示の単純さにも拘わらず力学系としては複雑な挙動を示しうることが知られている。また例えば、パラメータbを固定してaを動かした時、aの値が十分小さければ非遊走集合は空、十分大きければ力学系はhorseshoeと同値になる。このように、Lozi familyを一次元単峰写像族の二次元における対応物の典型例と捉えることも出来るであろう。

　本論文の目標は、このようなLozi familyに対してkneading理論のアナロジーを構成することにある。このkneading理論とは、MilnorとThurstonによって創始された、一次元力学系(特に単峰写像)に対する解析の基本的な手法の一つである。ラフに言ってこの理論は、「写像のcritical pointの挙動を示す記号列が力学系の位相的性質を決定する」ということを主張している。しかしLozi写像は同相写像のため通常の意味でのcritical pointを持たず、また一次元理論で重要であった区間の持つintrinsicな順序構造が二次元では明らかではない等、その理論の高次元化には幾つかの困難が存在する。そこで筆者は、数理物理学者Cvitanovicらのアイデアに基づき、以下のようなkneading理論をLozi familyに対して構成した。基本的なアイデアは、Lozi写像を"不完全な"horseshoeと見なしてその"不完全さ"をpruning frontと呼ばれるものを用いて測る、ということである。

　以下では常にを仮定する。このとき、の殆ど全ての点でhyperbolic cone fieldが存在する。まずLのK集合(前方軌道も後方軌道も有界に留まる初期点全体;strange attractorやすべての周期点を含み、位相的エントロピーもこの上の力学系だけで決定される)に注目し、相空間をy-軸(Lがsingularな部分)で分割することにより記号空間への対応:K{+1,-1}^Z

　を構成する。筆者は、対応の"逆写像"(これはJ.Milnorからのsuggestionをもとにして構成した)を用いることにより、Lozi写像に対するkneading列として以下のDefinition 1.1にあるような記号空間内の二つの部分集合のペアpruning pair(P,D)を定義した。

　このpruning pairには、以下のような幾何学的解釈も可能である。いま一点X∈Kを取り、その軌道がy-軸に集積していないとする。この時Xにおける局所不安定(resp.局所安定)多様体が存在するが、これはLozi写像の区分線形性より線分になる。そこでこの線分を含むような直線を考えよう。この直線とx-軸との交点p(resp.q)はhyperbolic cone fieldを用いて具体的に計算が可能で、実際a、b、＝(X)のみを用いた連分数を使って表現される。更に重要なことは、の仮定の下では、これらの値p、qの形式的表示は全ての記号列に対して((K)の元であるかないかにかかわらず)well-definedであるということである。

　Definition 1.1.

　をL_a,bのpruning frontと呼び、

　をL_a,bのprimary pruned regionと呼ぶ。(P_a,b,D_a,b)をL_a,bのpruning pairと呼ぶ。

　第一に問題となるのは記号空間内の部分集合(K)を特徴付けることにある。

　Theorem 1.2.集合(K)はDによって特徴付けられる。すなわち

　ここにはshift map:(…_-1・₀₁…)≡…_-10・₁….

　この定理は一次元のGuckenheimerの結果に対応しているばかりでなく、Cvitanovicらが提唱している"pruning front conjecture"の解答をLozi写像の場合に与えている。また前述のように、集合P、Dはパラメータa、bを用いた連分数展開を使って表現できるため、具体的に与えられたLozi写像の位相的エントロピーの数値的評価も可能である。

　Theorem 1.2を出発点として、筆者はpruning pair(P,D)のみを用いることによってLの力学系のtopological modelを構成した。より正確には、集合

　をP_a,bのみから定まる同値関係で割ったとき、その商空間上のshiftのfactorが元のK上の力学系Lと位相共役になる、ということが示せる(本文Theorem5.5参照)。この主張は、pruning pairがLの力学系のトポロジカルな情報を全て含んでいることを意味している。更に次のようなfirst tangency problemに対する肯定的解決を与えることができる。

　Theorem 1.3.H≡{(a,b)|L_a,bはfull shiftとtopologically conjugate}とする。このとき任意の(a,b)∈∂Hに対し、b>0(resp.b<0)ならL_a,bはheteroclinic(resp.homoclinic)tangencyを持つ。更にその時のL_a,bのcombinatricsはbの符号のみに依る。

　この定理の系として、

　Corollary 1.4.∂Hは代数的。

　実際∂Hはより具体的にわかり、例えばb>0ではで与えられ、またb<0では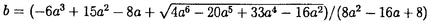となる。更にh(L_a,b)をL_a,bの位相的エントロピーとしたとき、

　Corollary 1.5.集合{(a,b)|h(L_a,b)がmaximal、i.e.log2}はHの閉包と一致する。

　現時点では、位相的エントロピーのパラメータ(a,b)に対する連続性の問題は未解決である事を注意しておく。

　また別の方向性の応用として、Lozi familyの分岐現象(パラメータに対する軌道の依存性)が解析可能である。

　Theorem 1.6&1.7.任意の固定されたbに対して＝(b)が存在してah(L_a,b)はa>で単調増加、非定数。更にこの族について、L_a,bの分岐も単調増加(すなわち各軌道はaを増やしたときに消滅しない)。

　実際、Hの外側からHの内側に入り∂Hに横断的な如何なる方向に対しても上の結論は成立する。また、いつ分岐が起こるか、その分岐のタイプとしてはどのようなものに限られるか、も決定した。特にこの単調性の成り立つ領域では、区分線形"saddle-node"タイプの分岐しか起こらず、"period-doubling"は起こらない。なお上述のような分岐現象の単調性は、Kan-Kocak-YorkeによるC³-diffeomorphismsの1-パラメータ族に対する反単調性定理(Ann.Math.1992)がLozi familyのような区分線形写像のカテゴリーでは必ずしも成立しないことを示している(b<0、(a,b)∈∂Hの時、L_a,bはhomoclinic tangencyを持つことに注意)。

　更に第九章ではp、qの具体的表示を応用してLozi写像のstrange attractorのHausdorff次元をパラメータのみ用いて評価し(Corollary1.8)、第十章ではpruning frontPがどのような幾何的性質を持つかを考察した。一般に、pruning frontの形は非常に複雑になりうる。そこで以下のようにpruning frontの"essential part"を取り出すことを考える。集合K∩{x＝0}をCとおき、Lozi写像のcritical setと呼ぶことにする。各点X∈L(C)に対して、Xを通る局所不安定多様体と、Xに収束するその上の点列{X_n}で、各X_nの軌道がy-軸と共通部分を持たないものを考える。この時(X_n)は唯一つの記号列からなり、{(X_n)}は記号空間内でwell-definedな極限を持つ。各Xを通る局所不安定多様体を全て考え、更にXがL(C)全体を走るときに得られる上述のような極限記号列全体をと書き、Lのunstably essential pruning frontと呼ぶことにする。一方、記号空間は二つのCantor集合の直積{+1,-1}^Z＝C^u×C^sとして表され、各Cantor集合に適当な順序を定義すると、記号空間上のshift mapの作用はいわゆるSmaleの標準的horseshoe写像になる。この時、

　Corollary 1.9.は、C^uからC^sへのある対称的単峰写像のグラフに含まれる。

　この描像はP.Cvitanovicによって予想されていたものである。とP∩Aの関連については本文を参照のこと。

　最終章ではK集合の構造について解析し、特に(Misiurewiczが扱ったパラメータの場合に)strange attractorの一意性の証明が得られた。

　論文提出者、石井豊は、提出論文において平面の上の区分線型な写像であるLozi写像

　$113115f11.gif$

　(ただし、a,b∈,b≠0.)の族についてそれが接空間のある種の双曲的分解をもつ場合に不変集合の記号力学系的表示を与え、それを応用して位相的エントロピーの性質やそのパラメータ依存性に関する結果を得た。この記号表現は、Henon写像(Lozi写像の定義においてをx²で置き換えたもの)に関するCvitanovicによるPruning Front Conjectureをある意味で実現、証明したものになっている。

　力学系理論の研究においては、相空間の軌道の構造が複雑であり、初期値のわずかなずれがその後の軌道に大きな影響を与えてしまうようないわゆるカオス的な力学系が一つの興味の中心となってきた。カオス的な力学系の研究はこれまで主に二つの方向に沿って進められてきた。一つは、双曲性をもつ力学系について研究するもので、かなり詳しい軌道構造の性質や構造安定性など、一般次元で理論が展開されている。もう一つの方向は、双曲性を仮定せず、その代わり、低次元で具体的でしかもある意味でカオス的力学系の典型となりうるような力学系(の族)について研究していくものである。

　双曲的な力学系とは、主な興味の対象となる不変集合(非遊走集合)上で接空間が二つの不変部分空間に分解され、力学系の作用によって一方の部分空間(不安定方向)のベクトルは引き伸ばされ、もう一方の部分空間(安定方向)のベクトルは縮められるようになっているもので、このような力学系は1960年代以降非常によく研究されている。特に、Sinai、Bowenにより導入されたMarkov分割の方法は非遊走集合をいくつかの部分集合に分割し、軌道がそのどれを通過するかによって記号力学系(記号列の空間上のずらし(shift)写像による力学系)と対応をつけ、それを通じて位相的エントロピーやエルゴード理論的性質などについての結果を得るというもので、非常に強力で豊富な道具を提供している。

　一方、双曲性をもたない力学系については、Markov分割あるいは記号力学系による表現の方法は一般に通用せず、それに代わる一般的な手法はまだ存在しない。そこで、現在では、カオス的で非双曲的な力学系を研究する方向としては、かなり具体的な力学系(の族)についての研究が主流となっている。この方向での主な研究としては、時間が離散的な場合(写像)については、実および複素1次元写像についてはかなり研究が進み、実および複素2次元の(微分)同相写像については集中的な研究が始まったばかりであり、時間が連続的な場合(微分方程式、流れ)については3次元までが主な研究の対象である。

　上でふれたHenon写像は、物理学等との関連で、そして平面の写像の中でシンプルな形でありながら複雑な力学系的世道をもつものとして、幅広く興味を持たれている。数値実験ではカオス的なStrange Attractorの存在が知られている。これに関する顕著な結果としてはBenedicks-Carlesonによる、非自明ではあるが、双曲的でもないStrange Attractorの存在証明があるが、詳細な軌道構造やパラメータ依存性についてまだよくわかっていない。それ以前に物理学者Cvitanovicは、1次元単峰写像系に対するMilnor-Thurstonによるkneading theoryの類似から、Henon写像の相空間を大雑把に2つに分けそれによって軌道を記号列で表現し、さらにこの記号列をSmaleの馬蹄型力学系(Horseshoe)の軌道とみなすことにより、Henon写像を「不完全な馬蹄型力学系」とみなすことを提案した。そして、馬蹄型力学系の軌道がいつHenon写像の軌道として実現されるかは非常にシンプルな形をした禁止領域(Primary Pruned Region、その境界がPruning Front)によって特徴づけられるのではないかというPruning Front Conjectureを提案した。これはいまだにその定式化の正当性も含めて未解決の問題である。

　この論文で取り扱われたLozi写像はHenon写像をもっと簡略化したモデルとしてLoziによって1978年に提案された。数値実験ではやはりStrange Attractorの存在が知られていたが、1980年Misiurewiczにより、パラメータに関する条件$113115f12.gif$の下で、接空間が双曲的分解をもつことが発見され、それを用いてStrange Attractorの存在が数学的に証明された。ただし、Lozi写像はこの場合、接空間が双曲的分解をもっていても、微分の不連続性から、上に述べたようなMarkov分割の方法が適用できず、普通の双曲的力学系の理論の枠組みでは取り扱いができなかった。

　論文提出者は条件$113115f13.gif$の下でLozi写像L_a,b:→に対して軌道が有界にとどまるような点の集合Kを考え、平面をy軸によってx座標が正の部分と負の部分に分け、Kの各点Xに対し、各時刻にその軌道がy軸のどちら側にいるかによって+1,-1からなる記号列を対応させてそれをitineraryと呼び、と書いた。ただし、y軸を通る軌道には+1,-1両方を対応させ、_LはKから{+1,-1}^Zへの多価写像となる。これがL|_Kの軌道の記号列表現であり、実は、位相的エントロピーなどの情報は_Lの像によって決定されることがわかる。しかし、一般にはすべての{+1,-1}^Zの元(記号列)が_Lの像として実現されるわけではなくこれを特徴づけるのが重要な課題となる。

　そのために論文提出者は{+1,-1}^Zの各元に対してLの「仮想軌道」を対応させ、それがいつ本物の軌道として実現されるかを考えた。(これは、J.Milnorにより提案されたものである。)実際には$113115f14.gif$に対して「仮想軌道」を定義し、その「仮想不安定多様体」、「仮想安定多様体」とx軸の交点としてを定義し、さらに、pruning front

　$113115f15.gif$

　とprimary pruned region

　$113115f16.gif$

　を定義した。これら定義の下、論文提出者は_Lの像が

　$113115f17.gif$

　(はずらし写像)と特徴づけられ、さらにP_Lのみによる同値関係〜pにより、K上のLとA_L/〜p上のとが位相共役になることを示した。さらに、は連分数型展開で表示することが可能であり、そのパラメータ依存性をある場合に明示的に評価することができた。その応用として論文提出者は以下のような結果を得た。

　馬蹄型領域の境界の特徴付け:_Lが全単射になるときL_a,bは馬蹄型(Horseshoe)であるといい、そのようなパラメータ(a,b)の集合をHと書く。このとき、その境界∂Hは実代数的曲線である(具体的表示が可能)。また、∂Hでの同値関係〜pはbの符号にのみ依存し境界点によらず決まり、それらは互いに共役な力学系を与える。(この〜pも具体的な表示が与えられた。)

　位相的エントロピーおよび周期点の分岐の単調性:∂Hの充分近くで、bを固定し、aを増加させたとき、の位相的エントロピーは単調非減少、また、一度発生した周期点がaの増加とともに消滅することはない。

　K_a,bのハウスドルフ次元:あるパラメータ領域でのK_a,bのハウスドルフ次元の上からの評価を与えた。

　これらの結果は、双曲性をもちながら微分の不連続性によって従来の双曲型力学系のような取り扱いができない場合にも、記号表現によるアプローチが可能であることを示しており、またエントロピーの部分的単調性は平面の可微分力学系の族におけるKan,Kocak,Yorkらによる反単調性(Antimonotonicity)の結果が区分的可微分系では成立せず、それと対照的な結果が得られることを示した。以上の理由により、これらの結果は今後の力学系研究において重要な意義をもつものと思われる。

　よって論文提出者、石井豊は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。