| 内容要旨 | | 組合せ最適化問題は,有限個の要素の組合せの集合上で定義された関数の,最大値ないし最小値を求める問題である.(以下,最大値に限定する.)組合せの数は有限であるが,構成要素数に対し"組合せ数"的に増大するため,全ての組合せを調べるという素朴で確実な方法は,実用的でない. 汎用ではないが実用的な方法に,次のような多面体的アプローチがある[3].組合せの有限個の構成要素の集合をSとしよう.Sの要素の一つの組合せは,Sの要素の各々に整数を割り当てる関数 (すなわち, (すなわち, )で表現できる.したがって,可能な組合せの全体を,|S|-次元ユークリッド空間RSの全整数格子点の,ある部分集合 )で表現できる.したがって,可能な組合せの全体を,|S|-次元ユークリッド空間RSの全整数格子点の,ある部分集合 で与えることができる.また,最大化する関数は,多くの場合,構成要素それぞれに実数を与える重み関数 で与えることができる.また,最大化する関数は,多くの場合,構成要素それぞれに実数を与える重み関数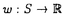 をもとに,組合せ をもとに,組合せ に対し, に対し, とxの内積 とxの内積 Txを割り当てるものである.このような関数は, Txを割り当てるものである.このような関数は, 上の線形関数になる.(この関数を 上の線形関数になる.(この関数を と書くことにする.)このような線形関数 と書くことにする.)このような線形関数 を,組合せ全体の凸包 を,組合せ全体の凸包 の上で最大化すれば,その値はもとの最適化問題の解と一致する.したがって,凸包を記述する不等式系が得られれば,組合せ最適化問題は,線形計画法に帰着する. の上で最大化すれば,その値はもとの最適化問題の解と一致する.したがって,凸包を記述する不等式系が得られれば,組合せ最適化問題は,線形計画法に帰着する. このアプローチには,凸包conv( )を記述する不等式系が必要であるが,そのような不等式系が元の組合せ構造から,容易には得られない場合もある.いくつかのケースでは, )を記述する不等式系が必要であるが,そのような不等式系が元の組合せ構造から,容易には得られない場合もある.いくつかのケースでは, が,組合せ構造から簡単に得られる不等式系を満たす,整数格子点の集合と一致する.このような場合の線形関数 が,組合せ構造から簡単に得られる不等式系を満たす,整数格子点の集合と一致する.このような場合の線形関数 の最大化問題は,整数計画法と呼ばれ,一般に解くのは,組合せ最適化問題と同程度に難しいことが知られている.ところで,組合せ構造から導かれる不等式系の実行可能解の集合の各頂点が,整数格子点であることが保証されていれば(このような不等式系はtotally primal intgralという),それが凸包と一致することが分かる.EdmondsとGilesは不等式系のtotal dual integralityという性質を導入し,線形計画法の双対定理を使って,totally dual integralである不等式系は,totally primal integralであることを証明した[1].Total dual integralityは組合せ構造と多面体を結びつけるという,重要な不等式系の性質として知られている. の最大化問題は,整数計画法と呼ばれ,一般に解くのは,組合せ最適化問題と同程度に難しいことが知られている.ところで,組合せ構造から導かれる不等式系の実行可能解の集合の各頂点が,整数格子点であることが保証されていれば(このような不等式系はtotally primal intgralという),それが凸包と一致することが分かる.EdmondsとGilesは不等式系のtotal dual integralityという性質を導入し,線形計画法の双対定理を使って,totally dual integralである不等式系は,totally primal integralであることを証明した[1].Total dual integralityは組合せ構造と多面体を結びつけるという,重要な不等式系の性質として知られている. 凸包conv( )を記述する不等式系を,容易に得ることができる組合せ構造の一つに,マトロイドがある.マトロイドの場合,ランク関数と呼ばれる{0,1}S(Sの部分集合全体)で定義される関数 )を記述する不等式系を,容易に得ることができる組合せ構造の一つに,マトロイドがある.マトロイドの場合,ランク関数と呼ばれる{0,1}S(Sの部分集合全体)で定義される関数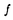 をもとに作られる不等式系 をもとに作られる不等式系  がtotally dual integralであり,したがって,凸包を記述する.この関数の満たす劣モジュラ性  をもとにしたマトロイドの拡張である,ポリマトロイド,劣モジュラシステム等は,マッチング,ネットワーク流,その他の構造を同時に扱える枠組となっている. マトロイドや,その拡張である,デルタマトロイド等の組合せ構造上の,線形関数の最適化は、多面体アプローチ以外にも,欲張り算法と総称される非常に単純で効率のよいアルゴリズムで,組合せ的に解けることが知られている.そればかりでなく,マトロイドやデルタマトロイドは,"最適化問題が欲張り算法で解ける,あるクラスの組合せ構造"として定義することもできる.また,劣モジュラ関数で作られる,不等式系(1)の実行可能解集合上での線形関数の最大化も,ある種の欲張り算法で解決できることが知られている.これは,欲張り算法の有効性を保証する,1対1交換可能性,およびその言い替えである関数の劣モジュラ性が,既知のマトロイド的構造に共通して存在するからである.なお,ここでいう1対1交換可能性とは, 二つの可能な組合せx,y∈ について,xの任意の構成要素u∈Sの数x(u)を,yのそれに1だけ近づけても,ある別の構成要素 について,xの任意の構成要素u∈Sの数x(u)を,yのそれに1だけ近づけても,ある別の構成要素 ∈Sの数x( ∈Sの数x( )も,同時にyの方に1だけ近づけて,可能な組合せにすることができる. )も,同時にyの方に1だけ近づけて,可能な組合せにすることができる. という性質のことである. この論文の目的は,劣モジュラ関数およびデルタマトロイドの1対1交換可能性を仮定しない拡張と,それに関連する最適化間題を解くアルゴリズムについて論じることである. まず,劣モジュラ関数の一般化が紹介される.マトロイドの1対1交換可能性は,劣モジュラ関数では,二つの面で反映される.一つは,不等式系(1)の各不等式の定める半空間が,01-ベクトルを法線とすることで,これは関数の定義域が{0,1}Sであることの帰結である.もう一つは,これらの半空間の交わり方が(2)から導かれる,良い交わり方をしているということである.本論文では,012-ベクトルで定義される関数の、良い交わり方をもたらす関数の性質  を提示している.(ここで,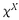 は,Xの特徴ベクトルを表す.)(3)は,ある種の増幅器付きネットワークから導かれる性質を,抽象化したものであることが明らかにされる.劣モジュラ関数の整数格子点への拡張としては,劣モジュラ関数のLovasz拡張[2]や,L-凸関数[4]が知られているが,(3)は,それらとは異なる拡張を与える性質である. は,Xの特徴ベクトルを表す.)(3)は,ある種の増幅器付きネットワークから導かれる性質を,抽象化したものであることが明らかにされる.劣モジュラ関数の整数格子点への拡張としては,劣モジュラ関数のLovasz拡張[2]や,L-凸関数[4]が知られているが,(3)は,それらとは異なる拡張を与える性質である. さらに,012-ベクトルの間にある半順序を定義し,"良い交わり方"を,この半順序の最大鎖を使って記述している.逆に,この"交わり方"をする不等式系を定めるならば,012-ベクトルで定義される関数は,(3)を満たすことも証明される. その後,最大鎖による特徴付けをもとに,この関数の定める不等式系上での線形計画法を,双対問題の側から解くアルゴリズムを提案する.このアルゴリズムを通じて,この関数から作られる不等式系がtotally dual integralであることが明らかにされる. 最後に,"分離定理"と呼ばれる,劣モジュラ関数やL-凸関数について知られている定理が,このような関数に対しても成立することを示す.この分離定理により,増幅器付きネットワークの可能な出力の集合が作る多面体が,{0,1,2}Sで定義された,(3)を満たす関数により,記述できることも示される. 続いて,マトロイド,デルタマトロイドを含むクラスである,2対2交換可能性が成立する組合せ構造の,最適化問題が論じられる. 欲張り算法は, に属する各組合せの間に,重み関数 に属する各組合せの間に,重み関数 から導かれる,ある辞書的順序の下で,最初になる組合せを解とするアルゴリズムということができる.ここで提案される弱欲張り算法は,少しアレンジした順序の下で,最初になる組合せを求めるアルゴリズムである.この順序は,辞書的順序とは異なり,全順序にならないため,複数の最適解の候補を扱う必要があるが,この解の候補間の辞書的順序を用いることにより計算のオーダーを落せることを示す. から導かれる,ある辞書的順序の下で,最初になる組合せを解とするアルゴリズムということができる.ここで提案される弱欲張り算法は,少しアレンジした順序の下で,最初になる組合せを求めるアルゴリズムである.この順序は,辞書的順序とは異なり,全順序にならないため,複数の最適解の候補を扱う必要があるが,この解の候補間の辞書的順序を用いることにより計算のオーダーを落せることを示す. さらに,このアルゴリズムが適用できる,2対2交換可能性を満たす組合せ構造の,ランク関数と,禁止マイナーによる特徴付けが,それぞれ述べられる. 参考文献[1]J.Edmonds and R.Giles.A min-max relation for submodular funcitons on graphs.In Annals of Disrete Mathematics 1,pages 185-204.North-Holland,1977.[2]L.Lovasz.Submodular functions and convexity.In Mathematical Programming-The State of the Art,pages 235-257.Springer-Verlag,1983.[3]M.Grotschel L.Lovasz and A.Schrijver. Geometric Algorithms and Combinatorial Optimization.Springer-Verlag,second corrected edition,1993.[4]Kazuo Murota.Discrete covex analysis.RIMS Preprint,No.1065,Kyoto University,1996. |