『大成算経』の編集意図については、建部賢明が記した『建部氏伝記』(1715)の中に記されている。すなわち、関と建部兄弟は当時の数学書に不備が多いことを嘆き、自らの数学的業績を集大成し、規範を示そうと図ったのである。当時和算家の間では、自著に解答を伏せた問題を読者に提示して解答を求めるという、一種の遊戯的な「遺題継承」という習慣が流行していたが、この習慣は殆ど無秩序な状態で行われていた。すなわち、解答が存在しない問題を提示したり、根拠も無しに他の和算書の問題・解答を誹謗するなどということが横行していたのである。(関孝和自身も、自著『発微算法』(1674)を佐治一平という者から誹謗されている。)このような状況の改善を目指し、『大成算経』は和算家が遵守すべき出題と解答の仕方をその内容に取り入れたのである。本論ではその証拠として、従来分析にかけられることの無かった「算数論」、「三要」、「題術弁」といった箇所をこの観点から読み解く作業を行い、『大成算経』と遺題継承の関連を明らかにした。

　本書の内容は大きく三つの部分に分けられる。すなわち、数学の基礎的計算技法を説明した「前集」(巻一より巻三)と、数学が扱うべき対象を説明した「中集」(巻四より巻十五)、そして、数学者が遵守すべき出題・解答の方法を述べた「後集」(巻十六より巻二十)である。この三部構成の中でも「後集」の内容は、『大成算経』独自のものであり、先に見た遺題継承の影響が濃厚に反映されていることが分かる。

　関、建部兄弟以後の世代の和算家は、『大成算経』が提示した「問題と解答の規範」を彼等の数学の基準として受け入れた。しかし、本書のその他の内容については、完璧に伝承されたわけではない。特に、角術の中の「定乗」という分野は理論の難解さもあり、早い時期に計算そのものが忘却されている。その復元を試みる作業が、本論の一つの主題である。

　和算における角術とは、正多角形を扱う理論のことであるが、具体的には以下の三つの要素の数値を求める計算である。

　(1)正n角形の内接円の半径(平径と呼ぶ)r

　(2)正n角形の外接円の半径(角径と呼ぶ)R

　(3)正n角形の面積S

　(3)のSについては、(1)のrを求めることによって簡単に算出できるので、角術の内容は実質的に(1)と(2)が主題となる。そこで、平径と角径の数値解を求めるために、種々の補助未知数(下図参照)を導入して高次方程式(開方式)を立て、Ruffini-Horner法と類似の算法を用いたのである。

[図]

　関と建部兄弟はrとRを求める算法の他に、『大成算経』において別種の問題を提起する。すなわち、正n角形において、そのrとRが満たすべき既約方程式の次数はどのような値となるか、という問題である。(この次数は「定乗数」と呼ばれ、現代的な次数の数え方よりも1だけ小さい値となる。)この問題に対して、『大成算経』は次のような結果のみを提示する。以下、平径の開方式の定乗数をJ_h、角径の開方式の定乗数をJ_kとする。

　i)nが奇数のとき:J_h＝J_k＝(n)-1.(但し(n)はnのオイラー関数)

　ii)nが4の倍数ではない偶数のとき:

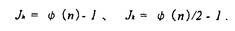
　iii)nが4の倍数のとき:

　関と建部兄弟がこれらの結果に到達した経緯は、和算史上の未解決問題であった。本論では以下のような仮説を構成し、この計算法を説明する。

　仮説は、二つの部分より成る。

　仮説I)正多角形の角数nに奇数の約数が無い場合、定乗数の値は素朴な帰納法に基づいて算出された。

　仮説II)角数nに奇数の約数が有る場合の定乗数の値は、可約な方程式を既知の既約方程式によって割る操作、「約式」に基づいて算出された。

　上で場合分けしたi),ii),iii)について仮説を適用すると、次のようになる。

　i)奇数nが素数の場合、一般に次の式が成立する。

　(但し、数列{k(i)}(1≦i≦s)は、k(1)＝(n-1)/2,

　k(i+1)＝k(i)/2[k(i)が偶数の場合]、

　k(i+1)＝(n-k(i))/2[k(i)が奇数の場合]、

　k(s)＝1によって定義する。)

　この式の補助未知数r_k(1),r_k(2),……,r_k(s)を消去することにより、rまたはRのみの方程式を構成する。その際、『大成算経』の編者らは各r₁にR^i-1を掛けて式変形するという操作を行っていた。(必要に応じてa₁を導入する場合があるが、それにはR^i-2を掛けて消去する。)この一連の式変形において不完全ながら、帰納法が用いられている。この式変形の結果より、最終的に得られる方程式の次数を計算することが可能となる。

　例として正11角形を挙げる。

　正11角形において、R⁵＝32r₅r₃r₄r₂rが成り立つ。これに式変形を施し、R¹⁰＝4r₅R⁴・r₃R²・a₃R＝(R⁴-3a²R²+a⁴)(4R²-a²)(3R²-a²)(R²-a²)というRの方程式を得る。(同様にしてrの方程式も得られる。)ここでr₅,r₃,a₃の三つの文字を消去するためにR⁵が最初の式に掛けられ、全体が10次の方程式となる。(J_h＝J_k＝9.)

　nが奇数の合成数の場合は、a_nR^n-1を式変形して得られるRのみの多項式(汎式N_n(R))をnの約数の汎式によって割り、最終的なRの方程式を得る。(この操作を「約式」と呼ぶ。rの方程式についても同様の操作を行う。)正15角形の場合は次のようにして定乗数を計算する。

　ここで、N₁₅(R)＝N₃(R)・N₅(R)・(R⁸-8a²R⁶+14a⁴R⁴-7a⁶R²+a⁸)＝(3R²-a²)(5R⁴-5a²R²+a⁴)(R⁸-8a²R⁶+14a⁴R⁴-7a⁶R²+a⁸)である。

　R⁸-8a²R⁶+14a⁴R⁴-7a⁶R²+a⁸＝0としたものが、正15角形の角径の方程式である。この定乗数は約式を行う過程で、14-2-4-1＝7＝(15)-1として求められる。このように約式の操作を前提とすることにより、定乗数が計算可能となる。

　ii)n＝2(2i+1)の場合、結果のみ述べれば次のようになる。この角数の正多角形に関して、次の関係式が成立する。

　これらの式に含まれている補助未知数を消去することにより、rまたはRの方程式を得る。その式変形の過程で仮説I)または仮説II)を適用し、所期の定乗数が得られる。

　iii)n＝4iの場合、やはり結果のみを述べると次のようになる。この角数の正多角形に関して、次の関係式が成立する。

　前者の式からrの方程式を、後者の式からRの方程式を導くが、その式変形の過程で仮説I)または仮説II)を適用することにより、所期の定乗数が得られる。

　以上が、本論の仮説に基づく定乗の計算法の概略である。

　『大成算経』の本文には、流伝の過程で様々な変更が加えられてきた。特に巻十一の「角法」の後半部分は、殆ど原形を留めないほどの改変が為された写本も存在する。関と建部兄弟が最初に記した内容を知るためには、諸写本間の校合作業が不可欠である。本論ではこの作業を実行し、ほぼ完全な形の本文を決定することができた。さらにこの調査の過程で、東京大学総合図書館に従来知られていなかった『大成算経』の写本が存在することが判明し、その内容を検討した結果、最も『大成算経』の原型に近いものであることが明らかとなった。

　本論は『大成算経』が有する数学史上の未解決問題の幾つかに解答を与える事により、斯学の発展に些かの寄与を為し得たものと信ずる。