| 内容要旨 | | 近年の結晶成長技術と微細加工技術の発展により、様々な人工低次元系が実現されるようになった。アンチドット格子とは、周期的なドット状の斥力ポテンシャル(アンチドット)により変調を受けた2次元電子系である。GaAs/AlGaAsヘテロ構造に作られる典型的なものでは、フェルミ波長が500Å程度、アンチドットの直径は1000Å程度、ポテンシャル周期は2000Å〜1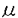 m程度であるため、短周期の系は半古典的な領域にあり量子効果が現れる。 m程度であるため、短周期の系は半古典的な領域にあり量子効果が現れる。 一様な磁場中での現象に興味が持たれており、磁気輸送現象では、アンチドット格子とサイクロトロン軌道の整合性に起因した磁気抵抗のピーク構造("整合ピーク")や、そこに現れる振動現象("アハラノフ-ボーム(AB)効果型振動")、アルトシュラー-アロノフ-スピバーク(AAS)振動などが観測されている。また、この系は古典的にはカオス系であり半古典領域での量子効果は量子カオスの観点からも興味が持たれている。 本論文では、磁場中のアンチドット格子の輸送現象に関する数値的な研究を行った。 我々はアンチドット格子を量子交差点の2次元配列でモデル化し、交差点での散乱を表す散乱(S)行列を用いた定式化を行った。この方法により大幅な計算時間の削減ができる。 サイクロトロン軌道の直径とポテンシャル周期が一致する整合条件(2Rc=a,Rc:サイクロトロン半径、a:ポテンシャル周期)が成立する磁場では、アンチドットの周りを回る軌道が輸送現象に影響を与えているのではないかと考えられている。 図1(a)は、その磁場での量子力学的状態密度(実線)と半古典論による結果(破線)を比較したものである。半古典論では、状態密度への寄与は各周期軌道(図1(b)参照)からの寄与の重ね合わせである。この結果、フェルミ面付近の構造はアンチドット格子の周りを回る周期軌道(図1(b)中の軌道(b))の寄与によって主に決められていることが確認された。この理由として、この軌道が他の軌道に比べて安定性が高いからであることが分かった。  図1(a)(左図a)量子力学的状態密度と半古典論との比較。実線は量子論、破線は半古典論の結果。右側の線は各軌道((b)図参照)の量子化準位を示す。(左図b)各軌道のリヤプノフ指数u。u=0で安定軌道を示す。(b)(右図)アンチドット格子における周期軌道。磁場2Rc=aでは、軌道(b)が安定であり電子状態に大きく寄与する。 図1(a)(左図a)量子力学的状態密度と半古典論との比較。実線は量子論、破線は半古典論の結果。右側の線は各軌道((b)図参照)の量子化準位を示す。(左図b)各軌道のリヤプノフ指数u。u=0で安定軌道を示す。(b)(右図)アンチドット格子における周期軌道。磁場2Rc=aでは、軌道(b)が安定であり電子状態に大きく寄与する。 図2は縦抵抗の磁場依存性の結果で、(a)は不純物散乱、(b)はアンチドットポテンシャルのゆらぎによる散乱の場合の結果である。(a)では、整合条件の磁場でピーク構造に非常に大きな振動が長い平均自由行程(le/ a=4)の結果にあらわれている。現実では平均自由行程はもっと長いにもかかわらず、大きな振動があらわれないことから、アンチドットのゆらぎによる散乱のモデルがより現実的であることが分かる。 a=4)の結果にあらわれている。現実では平均自由行程はもっと長いにもかかわらず、大きな振動があらわれないことから、アンチドットのゆらぎによる散乱のモデルがより現実的であることが分かる。  図2アンチドット正方格子の縦磁気抵抗の磁場依存性(a)(左図)は不純物散乱のモデル、(b)(右図)はアンチドットポテンシャルのゆらぎによる散乱のモデルである。縦線は周期軌道の量子化の位置を示す。実線は安定軌道を、破線は不安定軌道を示す。 図2アンチドット正方格子の縦磁気抵抗の磁場依存性(a)(左図)は不純物散乱のモデル、(b)(右図)はアンチドットポテンシャルのゆらぎによる散乱のモデルである。縦線は周期軌道の量子化の位置を示す。実線は安定軌道を、破線は不安定軌道を示す。 図中の縦線はアンチドットの周りを回る軌道の量子化準位がフェルミ準位をよぎる磁場を示したものである。縦抵抗にあらわれる振動と、周期軌道の量子化準位とはよく対応しているように見える。しかし、低磁場では振動の山が、整合条件付近の磁場では振動の谷が量子化準位と対応するなど、複雑な振る舞いを示しており、その機構はよく分かっていない。 現実のアンチドット格子は必ずドットの不規則さを伴うために、電子のアンダーソン局在が観測される。アンチドット三角格子におけるアンダーソン局在をサウレス数の方法を用いて調べた。 図3(a)はサウレス数の系の大きさ依存性のゼロ磁場付近での計算結果である。各系の大きさに対してサウレス数がAAS振動と同周期で振動する結果が得られた。この結果から見積もられた局在長の逆数を示したものが(b)図である。  図3(a)(左図)サウレス数の磁場依存性。いくつかの系の大きさ(4×2,8×4,12×6,16×8)に対して示してある。例えば、ゼロ磁場の結果は-0.0625< 図3(a)(左図)サウレス数の磁場依存性。いくつかの系の大きさ(4×2,8×4,12×6,16×8)に対して示してある。例えば、ゼロ磁場の結果は-0.0625< / / 0<0.0625の範囲に示される。(b)(右図)局在長の逆数の磁場依存性 0<0.0625の範囲に示される。(b)(右図)局在長の逆数の磁場依存性 サウレス数の振動を反映して局在長も同様の振動をする結果が得られた。 数値計算で得られた結果は実験結果と定性的に一致しているが、実験で見積もられた局在長はポテンシャル周期a程度であり、数値計算結果8a〜30aと比べると大きな差があり、今後の課題である。 |
| 審査要旨 | | 最近の半導体における微細加工技術の進歩に伴い,ミクロとマクロの中間のメソスコピック領域で様々な構造が実現できるようになった.このような系において電子がいかに振る舞い,量子効果がどのように現れるかを調べるための実験的,理論的研究が盛んに行なわれている.本研究はそのような系のうちでもアンチドット系と呼ばれるものを対象にしている.これは周期的なドット状の斥力ポテンシャルを2次元電子系に加えた系であり,斥力ポテンシャルの広がりは0.1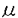 m程度であり,周期は0.2 m程度であり,周期は0.2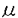 mから,l mから,l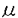 m程度のものが,本研究の対象である.磁場中でのこの系における様々な実験結果を,電子状態に対する数値計算の結果より理解しようと試みたのが本論文であり,英文で6章からなる. m程度のものが,本研究の対象である.磁場中でのこの系における様々な実験結果を,電子状態に対する数値計算の結果より理解しようと試みたのが本論文であり,英文で6章からなる. 序論の第1章に続く第2章において,本研究の対象となるアンチドット系におけるいくつかの実験結果が,本研究以前の理論的な解釈を含めて述べられている.即ち,電気抵抗における整合ピークとこれに重なって観測されるAharonov-Bohm型の振動現象,より低磁場で観測されるAl’tshuler-Aronov-Spivak振動,Anderson局在領域における電子の局在長の振動,がこれらの実験結果である.これらのうち,整合ピークの原因は既に磁気収束の効果であることが明らかにされており,Al’tshuler-Aronov-Spivak振動についても数値計算で再現されているが,Aharonov-Bohm型振動の原因は未解明であり,局在長の振動現象についても理論的な解明がなされていないという本研究以前の現状の紹介が行なわれた. 第3章以下では本研究の結果が述べられるが,先ず,本研究における独創的な点である数値計算の手法が記述されている.即ち,アンチドット格子を交差点が周期的に配置されたものと見做し,一つの交差点に対するS行列を用いて,系全体の電子状態を求めるという手法が紹介される.この方法の利点は計算時間の大幅な削減をもたらすことで,この結果大きな系や,特に磁場とアンチドット格子が簡単な整合関係にない系での計算が可能となった.第3章の残りの部分では,この方法で得られる電子の状態密度が厳密対角化の結果と良い一致を示すことが明らかにされ,更に結果の半古典論による解釈が行なわれている.また,Boltzmann方程式の緩和時間近似による伝導率の計算が行なわれ,伝導率のFermiエネルギー依存性と状態密度のエネルギー依存性には明確な対応関係は存在せず,状態密度により抵抗の振動現象を理解することはできないことが明らかにされた. 第4章ではS行列の方法でのLandauer公式による電気抵抗の計算結果が述べられている.ここでは不純物散乱の強さや,アンチドットポテンシャルの揺らぎの大きさを変えた場合に整合ピークの大きさがどのように変化するか,Aharonov-Bohm型の振動がいかに現れるかについての議論が行なわれている.アスペクト比と呼ばれるドットの直径dとドットの周期aの比を変化させた計算も行ない,d/a>0.7では整合ピークとAharonov-Bohm型の振動が共に消失することから,これらの現象の原因として,それぞれ拡散型の軌道の存在と周期的軌道の存在を推測した.しかし,Aharonov-Bohm型の振動については振動の起こる機構を特定するには至っていない. 第5章ではThouless数の計算が行なわれ,これを用いて電子の局在長が計算された.これらは,アンチドット格子の単位胞中の磁束と共に振動し,周期は量子磁束の半分であることが示された.この結果は本研究においてはじめて得られたものであり,本論文の重要な成果として評価できる.但し,振動の周期は実験結果と一致しているが,局在長の絶対値は実験とは1桁以上の違いがあり,この違いの解明は今後の課題として残されていることが述べられている. 以上述べてきたように,本研究で論文提出者が開発したアンチドット格子に対する効率的な計算方法とその結果得られた多くの新たな知見は今後この分野の研究の進展に大いに貢献するものと審査員全員により認められた.なお,本論文第3,4章および第5章は,指導教官安藤恒也教授他との共同研究であるが,論文提出者が主体となって計算及び解析を行ったもので,論文提出者の寄与が十分であると判断する.従って本論文は博士(理学)の学位論文として合格であると判断する. |