一次元、及び擬一次元の反強磁性ハイゼンベルグ模型は古くから研究されているが、最近の実験技術の発達や、理論的に厳密な、もしくはかなりしっかりした理論が構成できることなどから、現在でも広く研究されている対象のひとつである。これらの模型は、以下の点において非常に興味深く、物理的に面白い。

　・低次元のため、非常に強い量子効果が期待される。

　・共形場理論により臨界現象の構造がきれいに表現され、ユニバーサリティーの議論ができる。

　・ベーテ仮設法による厳密解や、Valence-Bond-Solid模型に代表されるmatrix product ground stateを持つ模型など、厳密に解ける模型があり、それらについて様々なことを厳密に知ることができる。

　この学位論文では、一次元、及び擬一次元の反強磁性ハイゼンベルグ模型(AFH)の基底状態における、いくつかの理論的な側面について考察する。考えるハミルトニアンは、最近接相互作用をもつAFH梯子模型で、

　である。但し、であり、相互作用は反強磁性的(J₁,>0)とする。S_n,iはSU(2)の3つの生成子で、その大きさはSである。つまり、S_n,i・S_n,i＝S(S+1)。添え字のi,jとn,mはそれぞれ鎖方向と、桁方向のサイト番号を表わす。ここでNを梯子模型の足の数とし、N’は桁方向の境界条件によりN’＝N-1(自由境界、この場合をopen ladderと呼ぶことにする。)またはN’＝N(周期境界、但し、N≡N+1、cylindrical ladder)とする。さらに議論の展開上、次近接相互作用も導入する。

　つまり、全体のハミルトニアンは＝₁+₂である。

　まず、擬一次元の時にも重要な手法となる場の理論をレビューしながら、一次元鎖の場合(N＝1)について考察する(第2章)。一次元のAFH模型においてみられる興味深い現象の一つがHaldane conjectureである。それによれば、基底状態において、S＝半奇整数の時は励起にギャップレスのモードがあり、スピン相関関数は冪的に減衰する。それに対して、S＝整数の時は励起にギャップがあり、スピン相関関数は指数的に減衰する。S＝半奇整数の臨界的な場合には、その最小の量子数S＝1/2の場合に、ベーテ仮設による厳密解があり、また、ボゾン化法と共形場理論によりかなり精密な議論が為されている。S＝1/2AFH鎖には様々な物理量に対数補正項が現れることが知られているが、この項の存在は重要な意味を持つことも多い。低エネルギーの極限で本質的にS＝1/2AFH鎖はスケール不変のレベル1SU(2)WZW模型により表現されることが分かっているが、実際にはそれに加えて重要な項であるmarginally irrelevant operatorも存在し、この項が対数補正項を導き出す。この章では、自由境界と周期境界条件双方について、対数補正項のベーテ仮設による導出、及び、より一般的にボゾン化法を用いてレベル1SU(2)WZW模型+marginally irrelevant operatorで表わされる模型のエネルギーレベルスペクトルを詳しく解説する。この議論は、第3章でopen ladderを考察する時に重要である。さらにこの章では一次元の模型の中で上に書いたものとはまた別のクラスに入る模型である、Majumdar-Ghosh model、但し、S＝1/2)を紹介する。次近接相互作用が入ったことによりフラストレーションが入る。これにより相互作用が最近接だけの時とは状況が劇的に変わり、基底状態は厳密に2重に縮退して並進対称性が破れ、励起にギャップが存在する。Affleck-Liebの定理(基本的に、Lieb-Schultz-Mattisの定理)のいうところの"対称性が破れてギャップがある"という選択肢をとるよい例である。

　続いてこの論文のメインテーマである梯子模型を考える(第3章)。以下では特にS＝1/2の場合に焦点を絞って考える。現在まで、梯子格子上のAFH模型、特にopen ladderの研究は広く為されてきている。J₂＝0でopen ladderの時はS→∞の古典極限で、Neel orderが仮定できるので、一次元の場合と同様にNLMを用いた解析が行われている。それによれば、(S＝1/2の時も正しいとすれば)、N＝奇数の時は、励起にギャップがなく、N＝偶数の時はギャップがある。N＝奇数の時はAffleck-Liebの定理のいうところの"基底状態は縮退せず、励起にギャップがない"という選択肢をとり本質的にS＝1/2AFH模型と同じユニバーサリティーに属する。しかし、梯子模型の場合は桁方向の自由度があり、周期境界条件をとった場合、特にN＝奇数の時には、フラストレーションができるので状況が変わる、つまり強い量子揺らぎが状況を変えることが期待される。実際にN＝奇数の時は、open ladderの場合と違い、cylindrical ladderの基底状態は2重に縮退して並進対称性が破れ、励起にギャップが存在することを示すことができた。つまり、Majumdar-Ghosh modelと同じくcylindrical ladderの基底状態はフラストレーションによりダイマー化したもので、Affleck-Liebの定理の"対称性が破れてギャップがある"という選択肢をとる一つの例となるのである。

　この結論を導くために以下のような議論をした。

　J_⊥が小さいときには、これを摂動と考えることができると期待されるが、この摂動は繰り込み群の意味でrelevantな相互作用である。つまり、繰り込み群の流れはJ_⊥→∞に向っている。よって、まずは繰り込み群の固定点であると期待されるJ_⊥→∞の極限での系の性質を考えることにする。この極限では、まず各リング(周期境界を持つN-site S＝1/2AFH鎖)が独立の場合が出発点となる。奇数サイトのS＝1/2AFH鎖の基底状態は二つのダブレットが縮退(4重に縮退)している。(この事実には厳密な証明はないが、N＝3,5の手計算、N＝23までの数値厳密対角化による計算、およびNが充分大きいところでの場の理論による結果から任意のNについて成り立っていると考えられる。)その二つのダブレットのlattice momentumは0ではなく,かつお互いに逆の符号を持つ。(これら4状態を│↑L〉、│↓L〉、│↑R〉、│↓R〉と書く事にする。但し、L,Rは各々のmomentumの添字。)以下に見るようにこの4重の縮退がopen ladder(2重縮退)とcylindrical ladderの重要な相違点で本質的である。この4重に縮退した状態以外はO(J_⊥)だけエネルギーが高いので無視することができて、各リングに対し、4重に縮退した状態に作用する有効ハミルトニアンが構成できる。そのハミルトニアンは

　但し、で、⁺、^-はL,Rを入れ換える演算子。ここではNに依存した数で、例えばN＝3の時、＝4、N＝5の時、＝64/9である。

　この有効ハミルトニアンはJ₂＝J₁/2の時に、Majumdar-Ghosh modelの場合と同様の手法により厳密な基底状態を構成できて、基底状態はダイマー化したものとなる。この厳密に構成できた基底状態の波動関数は、site-localで最近接のサイトとしか相関を持たない(相関距離1)。このことから励起ギャップの存在が示唆される。J_⊥による摂動は非常に強く(スケール次元1)、J₂による摂動はmarginalであるので、一次元の場合と違って小さなJ₂の導入は系の本質的な性質を変えないと考えられ、J₂＝0の場合も基底状態はダイマー化したもので、励起にギャップがあると予想できる。この予想をDensity Matrix Renomalization Gruop algorithmによる数値計算を用いて、以下の点を調べることにより確かめた。但し、鎖方向には自由境界条件を使った。

　・基底状態の上に励起ギャップが存在すること

　・スピン相関関数が指数的に減衰すること(図1左)

　・波動関数がダイマー化していること(図1右)

　波動関数がダイマー化していることは、各々のボンドにあるエネルギー期待値を計るlocal-Hamiltonian operator H^r,r+1を定義して、この期待値が2重周期で、かつ減衰しないことを見ることによって調べた。open ladderの有効ハミルトニアンであるS＝1/2AFH鎖では、この期待値は冪的に減衰することが分かっている。上記の3点に対して、N＝3の時はこの事実をJ_⊥→∞の極限、及びJ_⊥が有限の場合について、Nが5以上の時にはJ_⊥→∞の極限について確認することができた。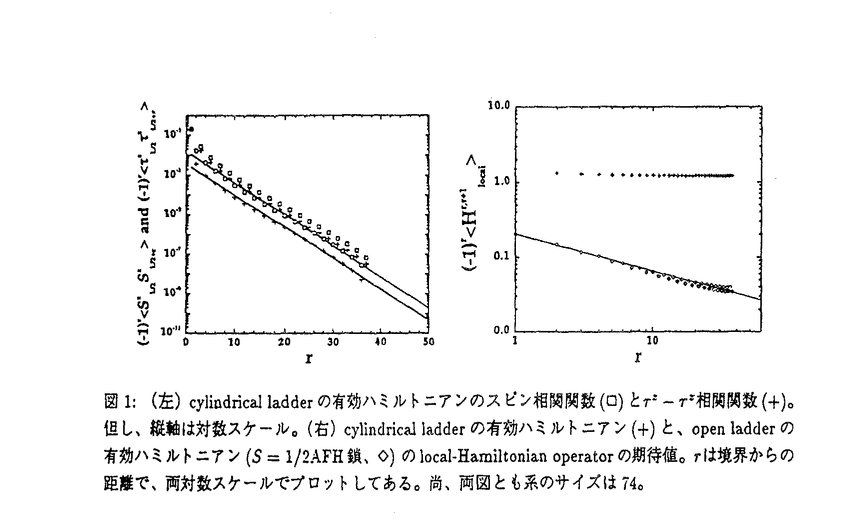

図表図1:(左)cylindrical ladderの有効ハミルトニアンのスピン相関関数(□)と^z-^z相関関数(+)。但し、縦軸は対数スケール。(右)cylindrical ladderの有効ハミルトニアン(+)と、open ladderの有効ハミルトニアン(S＝1/2AFH鎖、◇)のlocal-Hamiltonian operatorの期待値。rは境界からの距離で、両対数スケールでプロットしてある。尚、両図とも系のサイズは74。

　まとめると以下のようになる。桁方向に周期境界を持つN＝3の反強磁性ハイゼンベルグ梯子模型の基底状態は、ダイマー化していてthermodynamic limitでは並進対称性が自発的に破られる。基底状態と第一励起状態にエネルギーギャップがある。また、N>3でNが奇数の場合も、少なくとも強結合極限においてはダイマー化した状態が基底状態となる。この結果は桁方向に自由境界を持つ場合(本質的にレベル1SU(2)WZW模型)と対照的である。

図表

　スピン系の問題は昔から調べられているが、最近になって特にスピン・ギャップに関する問題が様々な局面で重要な問題になってきている。通常スピンに関して等方的なモデルでは、スピン波的な励起が生じてスピン励起にギャップは生じないと思われてきた。ところが最近、現実の物質においてギャップが生じる場合が数多く見つかってきており、この現象が自然界でしばしば現れるものであることを示している。更に、スピン・ギャップが開く場合は、ハルディン・ギャップ、梯子型ハイゼンベルグモデル、スピン・パイエルスの問題など、いずれも非常に面白い問題につながっている。

　とくに梯子型をした格子上のスピン系は、銅酸化物の1種として合成できることが示され、非常に興味が持たれている。理論と実験の解析の結果、梯子の脚が2本であるような普通の梯子型の場合、励起状態にギャップが開くということがわかってきている。以下、梯子の脚の数が偶数(N＝2,4,6,8…)のときは必ずギャップが開くのであるが、一方、脚の数が奇数のとき(N＝1,3,5…)はギャップが無く、ハイゼンベルグモデルと同様のスピン波励起があることが明らかになった。このような梯子の脚の数によってギャップのある無しが決まっているという現象は驚くべきことであった。

　以上が現在まで理解されていることであるが、本論文では奇数本脚の梯子の場合に梯子の桁方向について周期的境界条件を用いると、状況が一変してギャップが開くようになるという事を示した。これは、今まで全く予想されていなかった結果であり、大変興味深い。このギャップは桁方向のフラストレーションによって発生する新しい型のスピン・ギャップであると言える。第1章が序、第2章は一次元のスピン系のモデルについて、今までわかっていることをまとめた章である。第3章が本論文の主な部分で、桁方向が周期的な3本脚の梯子モデルについて調べている。第4章はまとめにあてられている。

　まず本論文では、くりこみ群によって桁方向の相互作用が強結合にくりこまれていくことを示し、その結果得られる強結合極限の場合を調べている。桁方向に周期境界条件を持つ場合、強結合の極限では桁方向の状態が4重縮退する。一方桁方向に開いた境界条件を用いた場合、縮退は$113198f08.gif$の2重のみである。この違いが本質的に重要で、スピン・ギャップのある無しを決めている。本論文では、この強結合極限の状態を用いて有効モデルを導出した。さらにある特殊な結合定数の場合に、基底状態がMajundar-Ghoshモデルと同じ手法で厳密に求まることを示した。Majundar-Ghoshモデルとは、フラストレーションのあるスピン1/2の1次元鎖のモデルであるが、基底状態は隣り合った2つのスピンが作るシングレット対の並んだもので表現され、スピン・ギャップが存在することが分かっている。従って、今の梯子型スピン系の有効モデルにおいても同様のスピン・ギャップが形成されていることが示されたことになる。

　さらに一般の結合定数の場合には、密度行列実空間くりこみ群という数値計算による手法を用い、やはりギャップが開いているということを示す事に成功した。具体的には、(1)無限系でのギャップの大きさの評価、(2)スピン相関関数が指数関数的に減衰すること、(3)基底状態の波動関数がシングレット対からなっていること、の3点について詳しく解析して確かめた。さらに桁方向が5本、7本など、一般に奇数の脚の数の場合にも同様のメカニズムによるスピン・ギャップが形成されるということを議論した。

　以上のように本研究では、梯子型スピンモデルにおける新しい形のスピンギャップ発現のメカニズムを理解するという目的のために、厳密に解ける場合と、それ以外の場合については数値的な手法を用いて詳しく調べた。このモデルに対応する実際の物質が存在するかどうかはわかっていないが、いくつかの重要な知見が本論文によって得られた。とくにスピン・ギャップの形成が境界条件の違いによるフラストレーションの効果によっても生じるということが示されたことは大いに評価される。

　本研究は高橋實教授との共同研究であるが、論文提出者は精密な数値くりこみ群の計算、結果の解釈、厳密に解ける場合との比較など本質的な寄与をしていると認められる。よって審査員一同は本論文が博士(理学)の学位を授与するのにふさわしいものであると認定した。