可解格子模型における解析的ベーテ仮説法や函数関係式は統計物理学のみならず差分方程式系の理論や数学の表現論にも影響を与えている。この論文では「ベーテ仮説法は統計物理学に応用するもの」といった固定観念に囚われず、可解格子模型から派生した差分方程式系の解や超リー代数sl(r+1|s+1)に対する解析的ベーテ仮説法の一般論を数理物理学的観点から研究した成果を発表する。 1994年に、国場、中西、鈴木は、可解格子模型における転送行列の満たす函数関係式系であるT-システムを提案した。T-システムは連続極限をとると、最も代表的な非線型可積分方程式の一つである、戸田場方程式に帰着することが知られている。一方、Reshetikhinによって提案された解析的ベーテ仮説法は、Bazhanov、Reshetihin、国場、鈴木らによってヤンギアンY(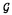 )(または量子アフィン代数Uq( )(または量子アフィン代数Uq(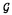 (1)))の基本表現に対して、組織的に研究されている。此処で、 (1)))の基本表現に対して、組織的に研究されている。此処で、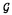 =複素単純リー代数Ar,Br,Cr,Dr,G2である。更に、 =複素単純リー代数Ar,Br,Cr,Dr,G2である。更に、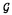 =Brの場合、一般の歪ヤング図形によってラベルされる表現に対しても解析的ベーテ仮説法の一般論が与えられている。 =Brの場合、一般の歪ヤング図形によってラベルされる表現に対しても解析的ベーテ仮説法の一般論が与えられている。 矩形のヤング図形によってラベルされる転送行列の包真空形式はT-システムの解を与えることが知られている。このことを手がかりにして、第二章では、解析的ベーテ仮説法の観点からD型の場合のT-システム(D型離散戸田場方程式)  の新しい解を求めた。B,C及びD型の古典単純リー代数に付随する離散戸田場方程式の解としては、国場、中村、広田による、行列要素が疎である行列式またはパフィアンによる解が知られている。B型の場合、国場、大田、鈴木による、其らとは異なる解もあり、行列要素が密であるという特徴がある。此処で我々が求めた解は、D型の場合の行列要素が密な解に相当する。其らが実際に関数方程式を満たしていることの証明はすべて、行列式に関するヤコビの恒等式に帰着するが、これはソリトン理論においては、よくあることである。実際に、国場、太田、鈴木は、量子アフィン代数Uq(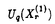 )に付随するT-システムが、離散戸田場方程式と看做せることを初めて指摘した。このことは、数学的には、離散ソリトン方程式の解と、ヤンギアンまたは量子アフィン代数の有限次元表現の指標との共通の構造を示唆している、と思われる。我々がここに提示した新しい解は、そのような共通の構造を例証していると考えられる。 )に付随するT-システムが、離散戸田場方程式と看做せることを初めて指摘した。このことは、数学的には、離散ソリトン方程式の解と、ヤンギアンまたは量子アフィン代数の有限次元表現の指標との共通の構造を示唆している、と思われる。我々がここに提示した新しい解は、そのような共通の構造を例証していると考えられる。 T-システムは複素単純リー代数のカルタン行列を用いて表現できることが知られている。このことに着目し第三章では、T-システムに於いて、複素単純リー代数のカルタン行列をアフィンリー代数のカルタン行列に置き換えることにより得られる、次の函数方程式について考察する。  此処で,   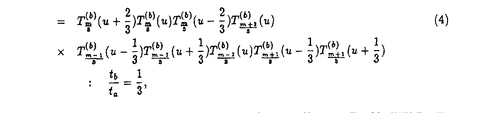 a∈{0,1,2,…,r}; (u)=1; (u)=1; (u)=1(m (u)=1(m Zの時);Iab=2 Zの時);Iab=2 ab-Bab(Iab=1,Dynkin図形のa番目のノードがb番目のノードと繋がっている場合;Iab=0,Dynkin図形のa番目のノードがb番目のノードと繋がっていない場合); ab-Bab(Iab=1,Dynkin図形のa番目のノードがb番目のノードと繋がっている場合;Iab=0,Dynkin図形のa番目のノードがb番目のノードと繋がっていない場合);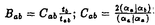 Cab:アフィンリー代数のカルタン行列; Cab:アフィンリー代数のカルタン行列; a:単純ルート); a:単純ルート); .この函数方程式は、連続極限をとると最も代表的な非線型可積分方程式の一つであるアフィン戸田場方程式に帰着する。通常のT-システムを漸化的に解くことにより得られる解は、(1)初期条件に関する多項式となる(2)行列式またはパフィアンを用いて表示することが出来るという二つの性質を持っているが、これら二つの性質は、此処で考察する函数方程式に対しても成り立っていることが判明した。我々は .この函数方程式は、連続極限をとると最も代表的な非線型可積分方程式の一つであるアフィン戸田場方程式に帰着する。通常のT-システムを漸化的に解くことにより得られる解は、(1)初期条件に関する多項式となる(2)行列式またはパフィアンを用いて表示することが出来るという二つの性質を持っているが、これら二つの性質は、此処で考察する函数方程式に対しても成り立っていることが判明した。我々は , ,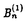 , , , ,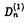 , , 及び 及び 型のアフィンリー代数に対するこれらの函数方程式の解を求めたが、その際、第二章で提示した解の表示式が重要な役割を果たす。 型のアフィンリー代数に対するこれらの函数方程式の解を求めたが、その際、第二章で提示した解の表示式が重要な役割を果たす。 前述のように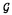 =リー代数に対しては、解析的ベーテ仮説法の系統的な一般論が存在したが、 =リー代数に対しては、解析的ベーテ仮説法の系統的な一般論が存在したが、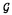 =超リー代数の場合、解析的ベーテ仮説法を個々の模型に対して個別に適用した例はあるものの、系統的に扱った研究はない。そこで第四、五章では、カルタン行列を用いて表現されたベーテ仮説方程式 =超リー代数の場合、解析的ベーテ仮説法を個々の模型に対して個別に適用した例はあるものの、系統的に扱った研究はない。そこで第四、五章では、カルタン行列を用いて表現されたベーテ仮説方程式  に基づいて、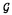 =超リー代数sl(r+1|s+1)に対する解析的ベーテ仮説法の一般論を系統的に展開する。超リー代数はリー代数の単なる一般化ではない。従って、「代数を取り替えただけで新しいものはない」という批判は当らない。実際に此処で扱う超リー代数は、(1)単純ルート系の取り方が一意的ではない、(2)非整数のKac-Dynkinラベルを持つ有限次元表現を構成できる、といった通常のリー代数とは異なる著しい特徴を持つ。 =超リー代数sl(r+1|s+1)に対する解析的ベーテ仮説法の一般論を系統的に展開する。超リー代数はリー代数の単なる一般化ではない。従って、「代数を取り替えただけで新しいものはない」という批判は当らない。実際に此処で扱う超リー代数は、(1)単純ルート系の取り方が一意的ではない、(2)非整数のKac-Dynkinラベルを持つ有限次元表現を構成できる、といった通常のリー代数とは異なる著しい特徴を持つ。 第四章では、一番目の特徴に留意しつつ、任意の単純ルート系によって表現されたベーテ仮説方程式に基づいて理論を展開する。先ず縦一列の超ヤング図形 = = , , =(1a)によってラベルされる転送行列の包真空形式Ta(u)を定義し、盤の和が標準盤に類似したある条件を満たすときベーテ仮説方程式を仮定すれば、極を持たないことを証明した。このことはTa(u)が転送行列の固有値であるための本質的に重要な条件である。更に超歪ヤング図形 =(1a)によってラベルされる転送行列の包真空形式Ta(u)を定義し、盤の和が標準盤に類似したある条件を満たすときベーテ仮説方程式を仮定すれば、極を持たないことを証明した。このことはTa(u)が転送行列の固有値であるための本質的に重要な条件である。更に超歪ヤング図形 ⊂ ⊂ によってラベルされる転送行列の包真空形式 によってラベルされる転送行列の包真空形式 を定義した。この函数は縦一列の超ヤング図形によってラベルされる転送行列の包真空形式を行列要素として持つ行列式として表わすことができるため、ベーテ仮説方程式を仮定すれば極を持たないことが言える。この函数 を定義した。この函数は縦一列の超ヤング図形によってラベルされる転送行列の包真空形式を行列要素として持つ行列式として表わすことができるため、ベーテ仮説方程式を仮定すれば極を持たないことが言える。この函数 は、スペクトルパラメータ依存性を除くと、超リー代数の表現の超指標を与える超対称Jacobi-Trudi公式に帰着する。このことは所謂指標極限の は、スペクトルパラメータ依存性を除くと、超リー代数の表現の超指標を与える超対称Jacobi-Trudi公式に帰着する。このことは所謂指標極限の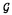 =超リー代数sl(r+1|s+1)の場合への一般化であると考えられる。超ヤング図形 =超リー代数sl(r+1|s+1)の場合への一般化であると考えられる。超ヤング図形 = = , , =(11)によってラベルされるR行列はパーク-シュルツ模型に相当するが、此処で我々が提出した新しい公式 =(11)によってラベルされるR行列はパーク-シュルツ模型に相当するが、此処で我々が提出した新しい公式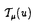 は、このR行列のフュージョンによって構成されたR行列による転送行列の固有値を与えるものと考えられる。実際に、此処でr=1,s=0, は、このR行列のフュージョンによって構成されたR行列による転送行列の固有値を与えるものと考えられる。実際に、此処でr=1,s=0, =(21)とすると、 =(21)とすると、 はPfannmullerとFrahmによる結果に(真空部分を除き)対応する。更に我々はr=1,s=0, はPfannmullerとFrahmによる結果に(真空部分を除き)対応する。更に我々はr=1,s=0, =(13),(12),(31)の場合について、 =(13),(12),(31)の場合について、 がパーク-シュルツ模型のR行列のフュージョンによって構成されたR行列による転送行列の固有値を与えることを確認した。尚、縦一列の超ヤング図形 がパーク-シュルツ模型のR行列のフュージョンによって構成されたR行列による転送行列の固有値を与えることを確認した。尚、縦一列の超ヤング図形 = = , , =(1a)によってラベルされる転送行列の包真空形式Ta(u)は、パーク-シュルツ模型の転送行列の固有値を与える公式に相当し、特にr=0,s=1及びr=s=1とすると其々、超対称t-J模型及び、Essler、KorepinとSchoutensよる超対称拡大ハバード模型の転送行列の固有値を与える公式を再現する。次に我々は、矩形の超ヤング図形 =(1a)によってラベルされる転送行列の包真空形式Ta(u)は、パーク-シュルツ模型の転送行列の固有値を与える公式に相当し、特にr=0,s=1及びr=s=1とすると其々、超対称t-J模型及び、Essler、KorepinとSchoutensよる超対称拡大ハバード模型の転送行列の固有値を与える公式を再現する。次に我々は、矩形の超ヤング図形 = = , , =(ma)に対する包真空形式の満たす函数関係式を導出した。この方程式は、s=-1とするとAr型の離散戸田場方程式に帰着する。又、相異なる単純ルート系に基づくベーテ仮説方程式の等価性について、超ワイル群との関連で議論する。其によると粒子空孔変換は長さが零の奇の単純ルートによる超ワイル鏡映に対応していることが判明した。 =(ma)に対する包真空形式の満たす函数関係式を導出した。この方程式は、s=-1とするとAr型の離散戸田場方程式に帰着する。又、相異なる単純ルート系に基づくベーテ仮説方程式の等価性について、超ワイル群との関連で議論する。其によると粒子空孔変換は長さが零の奇の単純ルートによる超ワイル鏡映に対応していることが判明した。 第五章では、超リー代数sl(r+1|s+1)の二番目の特徴に留意しつつ、連続パラメータに依存する有限次元表現に対する、解析的ベーテ仮説法の系統的一般論を与えた。頂上項仮説を考慮しながら、第四章で得られた行列式公式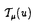 の連続パラメータcによる変形 の連続パラメータcによる変形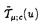 を考えた。このことは事実上、頂上項仮説の非整形式の最高ウエイトの場合への一般化を考えたことに相当する。更に連続パラメータに依存するベーテ仮説方程式を仮定すれば、 を考えた。このことは事実上、頂上項仮説の非整形式の最高ウエイトの場合への一般化を考えたことに相当する。更に連続パラメータに依存するベーテ仮説方程式を仮定すれば、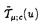 が極を持たないことを証明した。 が極を持たないことを証明した。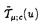 は非加法的な連続パラメータに依存する次数付きヤン-バクスター方程式を満たすR行列によって構成された転送行列の固有値を与えるものと考えられる。実際に此処でr=1,s=0, は非加法的な連続パラメータに依存する次数付きヤン-バクスター方程式を満たすR行列によって構成された転送行列の固有値を与えるものと考えられる。実際に此処でr=1,s=0, =(12)とするとPfannmullerとFrahmによる結果を再現する。 =(12)とするとPfannmullerとFrahmによる結果を再現する。 第四、五章で得られた結果は超リー代数sl(r+1|s+1)に関係する個々の模型から帰納して得られたものではなく、カルタン行列を用いて表現されたベーテ仮説方程式、頂上項仮説、指標極限などの概念を内省し、超リー代数sl(r+1|s+1)或いは其の量子変形の表現論を考慮しつつ一般化することによって構成的に得られた結果であることに注意しておく。尚、本論文は主に数理物理学的視点による論文ではあるが、第四、五章で得られた結果の特殊な場合は、高温超伝導の理論との関連で注目を集めている模型と関係している、という点でも重要であり、其らの理論の今後の発展の基礎となることが期待される。 |