組合せ論の分野で古くから考えられてきたタイリングの問題に対し、コンウェイは新しい代数的不変量"boundary invariant"を導入することで、そこから更なる発展を促した。ドミノタイリングの問題の場合、"boundary invariant"それ自体は自明な必要条件を導くのみだが、サーストンはその不変量を考える群"domino group"の構造を解析することで、必要十分条件を導くことに成功した。しかしここまでの議論は、正方格子上の単連結な領域に対するタイリングのみを対象にしたものであった。

　本論文では、サーストンの結果を向き付け可能な曲面にまで拡張する。すなわち、向き付け可能な曲面に対する、ドミノタイリングが可能であるための必要十分条件を与える。さらに、高次元における問題についてもまた、2次元の場合とほぼ同様の判定法により議論できることがわかる。

　タイリングの可否を考える曲面は、正方形をいくつか辺どうしで貼り合わせてできる向き付け可能な2次元多様体であり、チェッカーボードと同様に、辺を介して隣り合う正方形どうしは異なる色になるように2色で塗りわけられるもの(2彩色可能)とする。ドミノとは、ふたつの正方形を各々辺で貼り合わせて得られる2×1の長方形であり、タイリングとは、与えられた領域が、複数の小片(この場合はドミノ)からなる集合の元のある配置で、過不足なく覆い尽くされることである。

　定理を述べるにあたってはじめにいくつかの言葉を定義する(本論文第1節、以下同じ)。向きづけられた曲面Sは2彩色可能だから、白黒2色で塗り分けられているとする。

　定義 Sの各辺に対して、その辺の右側に白の正方形が位置する、またはその辺の左側に黒の正方形が位置するような向きをunderlying edge directionと定義する。

　定義p(₀,_n)が₀から_nへ至るedge pathであるとはp(₀,_n)がSの有向辺_ii+1を用いて、とあらわされる、S内の向きづけられたpathのことである。

　このときedge path p(₀,_n)の値〈p(₀,_n)〉を、

　によって定義する。ここに、右辺のは辺の値であり、

　によって定められたものである。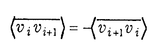に注意しよう。

　特に、edge path p(₀,_n)において始点と終点が一致する場合、すなわち_n＝₀の条件を満たすとき、p(₀,_n)はedge loopであるという。

　定義p(₀,_n)が₀から_nへ至るadmissible pathであるとはp(₀,_n)がSの内部においてはunderlying edge directionに従う、Sのedge pathのことである。

　定理4.1(主定理)向きづけられた曲面Sがドミノでタイリングできる必要十分条件は、S上のすべてのnull-homologous admissible 1-cycleに対し、その値が非負となることである。

　本論文ではこの定理の証明の前に、サーストンの与えた平面上の単連結領域に対する条件を、新しく定義した言葉("admissible"等)で言い換え(第2節)、次に一般の平面領域へ拡張する(第3節)。一般の平面領域の場合、定理は次のようになる。

　定理3.1平面領域Rがドミノでタイリングできる必要十分条件は、R上のすべてのnull-homologous admissible loopに対し、その値が非負となることである。

　証明は、十分性についてはRのhomology cover上に、その各頂点上に整数値を与える高さ関数を定義することで、被覆射像で不変なタイリングのひとつを構成的に与えることによる。必要性についてはすべてのnull-homologous admissible loopの値が非負であるn重連結な領域は、その一部を切り離して同じ条件のn-1重連結な領域へと変形できることを示す。これを繰り返せば、最終的にサーストンの示した単連結領域の場合に帰着することができる。

　勿論この場合の結果は、曲面に対する定理4.1に本質的に含まれている。

　定理4.1の証明は、タイリング可能ということが、グラフ理論における2部グラフの1-因子の存在と本質的に同値であることから、定理4.1の判定条件が、1-因子定理のそれと同値であることを示す。

　最後に第5節で、この種のタイリング問題を高次元のものへ拡張する。考える領域は、n次元立方体を、そのn-1立方体どうしを張り付けて得られる2彩色可能で向き付け可能なn次元多様体Mとし、この多様体を、ふたつのn次元立方体を、そのn-1立方体どうしを張り付けて得られるn次元ドミノによってタイルすることを考える。このとき、

　定理5.1向き付け可能なn次元多様体Mがn次元ドミノでタイリングできる必要十分条件は、M上のすべてのnull-homologous admissible n-1-cycleに対し、その値が非負となることである。

　証明は、定理4.1のものと同様である。

　最後に、3次元タイリングの問題を、2次元の問題に落とせる例を挙げておく。R³内のZ³に頂点を置く立法格子内の立方体からなる領域を考える。立方体の辺から6本をうまく選んでその頂点どうしを結ぶと、立方体の内部に正6角形が出来る。ひとつの立方体に対して正6角形の取りうる向きは4通りあり、隣り合う立方体の内部における正6角形どうしが互いに辺を共有し合うように配置することが出来る。立法格子全体にこの操作を施せば、2×2×2毎に切頭8面体が現れるような、正6角形からなる2次元多様体を得る。したがって、立法格子内の領域を3次元ドミノでタイリングする問題を、先に得られた2次元多様体の部分多様体を6角形ドミノ(ふたつの正6角形を、辺どうしで張り合わせたもの)でタイリングする問題に言い換えることができる。

　提出者は本論文において,タイル張りの構造をもつ曲面に対し,これがドミノタイルで敷き詰められるための必要十分条件を与え,かつこの結果を高次元に拡張している.

　平面上のタイル張りされた領域が与えられたとき,これがいつドミノタイルで敷き詰められるかという問題は古くから考察されてきたが,近年までの解析は初等的な段階に留まっていた.しかし1990年Conwayは,一般化したタイル張りの問題に対し,組み合わせ群論的な枠組と定式化を与え,平面領域に対して境界不変量を定義した.これは領域がタイル張り可能であるための必要条件となっている.古典的なドミノタイル張り問題の対象,すなわち白黒に塗り分けられた平面領域に対しては,この不変量は白黒のタイルの数の差を与えるものであり,旧来の研究の範囲を超えるものではなかったが,同年ThurstonはConwayの方法を発展させて,平面上の単連結領域がドミノタイル張り可能であるための必要十分条件を得ている.Thurstonの方法は,タイル張りの与えられた平面領域の各頂点に,基点から至る道を用いて高さ関数を定義し,これを利用して必要条件を記述し,かつドミノタイル張りをも構成するというものである.提出者はこの方法を解析することによって,その本質が零ホモローグな閉道に関する条件であることを見抜き,本論文ではこれを用いて,領域が多重連結の場合,さらには種数を持つ曲面の場合においても成立する正しい定式化を与えた.

　白黒のタイルで塗り分けられた平面領域あるいは向き付けられた曲面が与えられたとき,タイルの各辺の向きを黒のタイルの境界としての向きで定める.辺が白のタイルのみの境界である場合には境界としての向きの逆とする.またタイルの辺の和として表される閉道に対し,各辺の道としての向きが塗り分けから定まる向きと一致するか否かによって値±1を与え,その総和として閉道の値を定義する.この値は閉道が単連結領域の境界である場合にはConwayの境界不変量と等しい.さて道あるいは閉道が許容されるとは,道を構成する辺が曲面の境界以外にあるときその向きが常に塗り分けから定まる向きと一致するときをいう.また閉道の有限和を1-サイクルと呼ぶ.以上の定義のもとで提出者の結果は,与えられた曲面がドミノタイル張り可能である必要十分条件が,すべての許容される零ホモローグな1-サイクルが0以上の値をもつことで与えられるというものである.

　論文の前半はドミノタイル張りから条件が導かれることの証明と,多重連結な平面領域の場合に条件のもとでドミノタイル張りが存在することの証明に当てられている.ドミノタイル張りが与えられたとき,零ホモローグな閉道は,ドミノタイルの和となるような領域の境界となっているから,問題を各々のドミノタイルに帰着させることが可能で,これによって条件を導く.逆に条件が与えられたとき,領域の境界を結ぶ許容される道のうち,値の最も小さいものが存在する.このような道で与えられた領域を切断すれば,条件を保ったまま領域の連結数を減ずることが可能で,これを繰り返して単連結領域の場合に帰着する.切断に使う道は具体的に構成することが可能であるから,結局平面領域の場合にはドミノタイル張りを与えるアルゴリズムが存在することがわかる.

　後半では種数をもつ曲面および高次元化を扱う.この場合,条件のもとでタイル張りが存在することの証明は,平面領域のように単連結の場合に帰着させるのではなく,組み合わせ論でよく知られたTutteの補題,いわゆる結婚定理に帰着させる.Tutteの補題によれば,ドミノタイル張りが可能であるためには,白のタイルの任意の集合が与えられたとき,それに隣接する黒のタイルの総数が,もとの集合に属する白のタイルの数以上であればよい.ここで白のタイルの集合に隣接する黒のタイルをつけくわえた集合は曲面の領域をなし,幾何学的考察により,その境界は許容される零ホモローグな1-サイクルとなることがわかる.一方で領域の境界である1-サイクルの値は,領域内の黒のタイルと白のタイルの数の差であるから,Tutteの補題を適用することが可能となる.

　論文の最後は高次元への拡張に当てられている.Tutteの補題に帰着する方法は高次元のタイル張りの問題においても有効で,n次元の場合,1-サイクルをn-1-サイクルに置き換えるだけで結果が成立する.これは結果の単純な高次元化である.これに対し,3次元の立方体によるタイル張りが具体的に与えられた場合,各立方体に正六角形を埋め込むことによって,負曲率曲面の六角形によるタイル張りを考え,問題自体を2次元に帰着する方法もある.これは特殊な場合ではあるが,ホモロジー論における高次元のサイクルを1-サイクルに帰着する方法を示唆する可能性もある.

　以上に見てきたように,本論文は古典的なドミノタイル張りの問題に,位相幾何学的手法を導入するというまったく新しい試みであり,その美しい結果のみならず,今後の研究に新しい方向性を示唆する意味においても新しい知見を得たということができる.よって,論文提出者伊藤賢一は,博士(数理科学)の学位を受けるにふさわしい充分な資格があるものと認める.