| 内容要旨 | | 円周から円周への向きを保つ同相写像に対してPoincareはその写像による点の平均移動距離を表す位相不変量である回転数(rotation number)を定義したが、Newhouse-Palis-Takensはこの定義を拡張して円周上の写像度1の連続写像に対して回転集合(rotationset)を定義した。その後、n次元トーラス上の恒等写像にホモトピックな連続写像に対してKim,Mackey and Guckenheimer,Llible and Mackeyなどにより種々の回転集合が定義され、Misiurewicz and Ziemianは、系統的にこれらを整理した。1992年にはFranksとPollicottが独立に、種数が2以上の曲面に対して回転集合を定義したが、これら2つは定義が若干違っていた。これらすべての回転集合は恒等写像にホモトピックな写像に対して定義されたものであった。しかし回転集合は、定義によれば、多様体上の各点が写像によりどれだけ動くかをホモロジー的に計るものである。この論文では、写像のクラスを、1次元ホモロジー群へ誘導する同型写像が恒等写像となるような同相写像にまで広げて回転集合を新たに定義した。 一方、同相写像の力学系の研究を記号力学系の言葉に言い換えて、もとの写像の力学系の研究をする方法がある。記号力学系( A, A, )とは、有限個のアルファベットからなるアルファベット集合K={1,2,…,m}をとり、 )とは、有限個のアルファベットからなるアルファベット集合K={1,2,…,m}をとり、 =KZとして、 =KZとして、 の各点を各桁がKの成分からなる両側無限列で表し、 の各点を各桁がKの成分からなる両側無限列で表し、 上の写像として、シフト写像 上の写像として、シフト写像 、すなわち無限列の座標を左に1つずらすというものを考えるものである。このとき、 、すなわち無限列の座標を左に1つずらすというものを考えるものである。このとき、 不変な点列の集合 不変な点列の集合 Aを考えた( Aを考えた( A, A, )が記号力学系である。閉多様体M上の力学系(M,f)を記号力学系( )が記号力学系である。閉多様体M上の力学系(M,f)を記号力学系( A, A, )で表現するには、Mをマルコフ分割と呼ばれる有限個の長方形R1,R2,…,Rmに分割し、任意の整数nに対してfn(x)∈Riのとき )で表現するには、Mをマルコフ分割と呼ばれる有限個の長方形R1,R2,…,Rmに分割し、任意の整数nに対してfn(x)∈Riのとき n=i(ただし、ak∈{1,2,…,m})と定義して、点xのfの反復による挙動を両側無限列…, n=i(ただし、ak∈{1,2,…,m})と定義して、点xのfの反復による挙動を両側無限列…, -2, -2, -1, -1, 0, 0, 1, 1, 2,…で表現すれば良い。マルコフ分割は、Adler and Weissによって初めて2次元トーラスのアノソフ可微分同相写像に対する例が構成され、Sinaiにより一般のアノソフ可微分同相写像のマルコフ分割が系統的に定義された。また、Bowenは、Sinaiの方法を拡張し、公理A系に対して、非遊走集合を有限個の基本集合に分割し、その各基本集合上でマルコフ分割を構成した。Thurstonは擬アノソフ可微分同相写像に対するマルコフ分割を構成した。 2,…で表現すれば良い。マルコフ分割は、Adler and Weissによって初めて2次元トーラスのアノソフ可微分同相写像に対する例が構成され、Sinaiにより一般のアノソフ可微分同相写像のマルコフ分割が系統的に定義された。また、Bowenは、Sinaiの方法を拡張し、公理A系に対して、非遊走集合を有限個の基本集合に分割し、その各基本集合上でマルコフ分割を構成した。Thurstonは擬アノソフ可微分同相写像に対するマルコフ分割を構成した。 この論文では新たな回転集合の定義のもとで、多様体Mと同相写像fの対(M,f)がマルコフ分割Rを持つとき、Rと回転集合を関係づけ、回転集合を計算するアルゴリズムを与え、それを利用して1次元ホモロジー群へ誘導する同型写像が恒等写像となるような同相写像の回転集合が凸多面体になることを証明した。 Mを閉多様体、f:M→Mを同相写像で1次元ホモロジー群H1(M;Z)へ誘導する同型写像f*が恒等写像であるもの(以下ホモロジー自明という)、( ,p,M)を可換被覆空間のうち最大のものとする。この最大可換被覆空間 ,p,M)を可換被覆空間のうち最大のものとする。この最大可換被覆空間 上の被覆変換群D( 上の被覆変換群D( ,p,M)は、Mの整数係数1次元ホモロジー群H1(M;Z)と同型になり、自然に同一視できる。また、fがホモロジー自明であることから、被覆変換群D( ,p,M)は、Mの整数係数1次元ホモロジー群H1(M;Z)と同型になり、自然に同一視できる。また、fがホモロジー自明であることから、被覆変換群D( ,p,M)の任意の元hはfの ,p,M)の任意の元hはfの への任意の持ち上げFと可換になる。さらに、 への任意の持ち上げFと可換になる。さらに、 上の任意の閉曲線は、pによりM上の零ホモローグな閉曲線に写される。(M,f)の回転集合の定義は以下のようにする。 上の任意の閉曲線は、pによりM上の零ホモローグな閉曲線に写される。(M,f)の回転集合の定義は以下のようにする。 M上に基点Oをとる。fの への持ち上げの1つをF: への持ち上げの1つをF: → → とする。xの とする。xの への持ち上げの1つを への持ち上げの1つを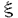 とする。 とする。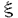 に一番近いp-1(O)の点 に一番近いp-1(O)の点 ( (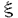 )と、Fn( )と、Fn(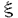 )に一番近いp-1(O)の点 )に一番近いp-1(O)の点 (Fn( (Fn(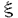 ))を結ぶ ))を結ぶ 上の曲線のpによる像はM上の閉曲線になるが、これをhn(x,f,F,O)とする。この閉曲線の1次元ホモロジー類を[hn(x,f,F,O)]とかく。( 上の曲線のpによる像はM上の閉曲線になるが、これをhn(x,f,F,O)とする。この閉曲線の1次元ホモロジー類を[hn(x,f,F,O)]とかく。( ,p,M)の性質から、[hn(x,f,F,O)]は ,p,M)の性質から、[hn(x,f,F,O)]は ( (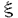 )と )と (Fn( (Fn(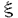 ))にのみ依存し、この2点の結び方にはよらない。このとき、 ))にのみ依存し、この2点の結び方にはよらない。このとき、 が収束する場合には、この値は基点Oの取り方によらないことが分かり、この値を が収束する場合には、この値は基点Oの取り方によらないことが分かり、この値を (x,f,F)とかき、xの回転ベクトルという。 (x,f,F)とかき、xの回転ベクトルという。 (x,f,F)はH1(M;R)の元である。回転集合Rot(f,F)を{ (x,f,F)はH1(M;R)の元である。回転集合Rot(f,F)を{ (x,f,F)|x∈M}で定義すると、これは実係数1次元ホモロジー群の部分集合になる。Fと異なるfの持ち上げF’をとったとき、 (x,f,F)|x∈M}で定義すると、これは実係数1次元ホモロジー群の部分集合になる。Fと異なるfの持ち上げF’をとったとき、 となるH1(M;Z)の元 となるH1(M;Z)の元 (F,F’)がxによらず一意に定まり、このことから、回転ベクトルおよび回転集合は、持ち上げの取り方によりH1(M;Z)の元の平行移動分の任意性がある事が分かる。この平行移動分の任意性を同一視したものの同値類{ (F,F’)がxによらず一意に定まり、このことから、回転ベクトルおよび回転集合は、持ち上げの取り方によりH1(M;Z)の元の平行移動分の任意性がある事が分かる。この平行移動分の任意性を同一視したものの同値類{ (x,f,F)|Fはfの持ち上げ}および{Rot(f,F)|Fはfの持ち上げ}をそれぞれ (x,f,F)|Fはfの持ち上げ}および{Rot(f,F)|Fはfの持ち上げ}をそれぞれ (x,f)およびRot(f)とかき、これらもそれぞれ回転ベクトルおよび回転集合とよぶ。 (x,f)およびRot(f)とかき、これらもそれぞれ回転ベクトルおよび回転集合とよぶ。 M上にf-不変な測度 が存在する場合、平均回転べクトル が存在する場合、平均回転べクトル を を で定義する。Birkhoffのエルゴード定理から、平均回転ベクトルは測度 で定義する。Birkhoffのエルゴード定理から、平均回転ベクトルは測度 に関してほとんどいたるxについて存在する。同値類 に関してほとんどいたるxについて存在する。同値類 を を とかき、この同値類も平均回転ベクトルという。平均回転ベクトルには、以下のような特徴がある。 とかき、この同値類も平均回転ベクトルという。平均回転ベクトルには、以下のような特徴がある。 命題(エルゴード定理) 平均回転ベクトルは と表される。 と表される。 つまり、平均回転ベクトルは、2点xとf(x)の への持ち上げ、 への持ち上げ、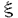 とF( とF(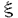 )にのみ依存する。この命題を用いると、次の定理を示すことができる。 )にのみ依存する。この命題を用いると、次の定理を示すことができる。 定理 f,gをM上のホモロジー自明な同相写像とし、共通な不変測度 を持つものとする。このときfとgの合成写像に対する平均回転ベクトル を持つものとする。このときfとgの合成写像に対する平均回転ベクトル は、 は、 と一致する。 と一致する。 この定理は、種数が2以上の閉曲面についてのFranksの定理の拡張になっている。 (M,f)がマルコフ分割R={R1,R2,…,Rm}を持つとき、任意の整数nに対してfn(x)∈Riのとき n=i(ただし、 n=i(ただし、 k∈{1,2,…,m})と定義すると、点xのfの反復による挙動は両側無限列…, k∈{1,2,…,m})と定義すると、点xのfの反復による挙動は両側無限列…, -2, -2, -1, -1, 0, 0, 1, 1, 2,…と表される。Mのマルコフ分割は 2,…と表される。Mのマルコフ分割は に持ち上げることができ、長方形Ri,Rjの持ち上げで、F( に持ち上げることができ、長方形Ri,Rjの持ち上げで、F( )∩ )∩ ≠0なる ≠0なる , , を取ることができる。この長方形 を取ることができる。この長方形 , , の内点Int の内点Int ,Int ,Int 上に代表点 上に代表点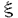 i, i,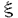 jをとり、これらの点に最も近いp-1(O)の点をそれぞれ jをとり、これらの点に最も近いp-1(O)の点をそれぞれ ( (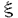 i)と i)と ( (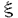 j)とする。この2点を結ぶ曲線のpによる像はM上の閉曲線となる。この閉曲線を j)とする。この2点を結ぶ曲線のpによる像はM上の閉曲線となる。この閉曲線を ijとかき、この閉曲線の1次元ホモロジー類を[ ijとかき、この閉曲線の1次元ホモロジー類を[ ij]と書く。( ij]と書く。( ,p,M)の性質から、[ ,p,M)の性質から、[ ij]は ij]は ( (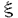 i)と i)と ( (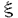 j)にのみ依存し、この2点のつなぎ方にはよらない。一方、回転ベクトルを定義したM上の閉曲線hn(x,f,F,O)は、始点を j)にのみ依存し、この2点のつなぎ方にはよらない。一方、回転ベクトルを定義したM上の閉曲線hn(x,f,F,O)は、始点を ( (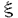 )、終点を )、終点を (Fn( (Fn(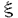 ))とする ))とする 上の曲線のpによる像であった。hn(x,f,F,O)は、 上の曲線のpによる像であった。hn(x,f,F,O)は、 と と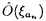 とを結ぶ曲線Anのpによる像で近似でき、p(An)のホモロジー類は、閉曲線の連結和 とを結ぶ曲線Anのpによる像で近似でき、p(An)のホモロジー類は、閉曲線の連結和 のホモロジー類と一致する。このことから、以下の定理が成り立つことがわかる。 のホモロジー類と一致する。このことから、以下の定理が成り立つことがわかる。 定理 ホモロジー自明な同相写像fの回転ベクトル (x,f)は、 (x,f)は、 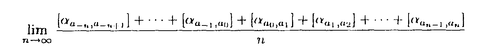 と表される。 M上の点xを記号力学系( A, A, )の点…, )の点…, -2, -2, -1, -1, 0, 0, 1, 1, 2,…で表したとき、長さ2の部分列-( 2,…で表したとき、長さ2の部分列-( i, i, i+1)を1次元ホモロジー群の元 i+1)を1次元ホモロジー群の元 に対応させる2ブロック写像をs:K×K→H1(M;Z)とする。上の定理は、回転ベクトルは、 に対応させる2ブロック写像をs:K×K→H1(M;Z)とする。上の定理は、回転ベクトルは、 A全体に対して、文字列から連続する2桁ずつとってsを施す写像S: A全体に対して、文字列から連続する2桁ずつとってsを施す写像S: A→(H1(M;Z))Zで与えられることを示している。これは、ソフィックシステムと呼ばれる系の典型例となっている。 A→(H1(M;Z))Zで与えられることを示している。これは、ソフィックシステムと呼ばれる系の典型例となっている。 一方、記号力学系( A, A, )の各点は、アルファベット集合Kの各元を頂点とする有向グラフ上の道で表現することができる。(M,f)の周期点はグラフ上の閉道に対応する。グラフ上の閉道のうち、同一の頂点を2つ以上含まないようなものを単純な閉道といい、対応する(M,f)の周期点を単純な周期点という。グラフ上のすべての頂点を通る閉道があるとき、このグラフを推移的なグラフといい、このとき(M,f)を推移的という。(M,f)が推移的なとき、(M,f)の任意の周期点に対する回転ベクトルは単純な周期点の回転ベクトルの組み合わせで作ることができ、周期点以外の点の回転ベクトルは周期点の回転ベクトルの組み合わせで近似できることから、回転集合は、単純な周期点に対応する回転ベクトルたちを頂点とした凸閉包で与えられることがわかる。グラフ上には単純な閉道は有限個しかないことから、単純な周期点も有限個しかなく、したがって、回転集合は実係数1次元ホモロジー群の凸多面体になることが分かる。この結果と記号力学系の性質から次のことが証明できる。 )の各点は、アルファベット集合Kの各元を頂点とする有向グラフ上の道で表現することができる。(M,f)の周期点はグラフ上の閉道に対応する。グラフ上の閉道のうち、同一の頂点を2つ以上含まないようなものを単純な閉道といい、対応する(M,f)の周期点を単純な周期点という。グラフ上のすべての頂点を通る閉道があるとき、このグラフを推移的なグラフといい、このとき(M,f)を推移的という。(M,f)が推移的なとき、(M,f)の任意の周期点に対する回転ベクトルは単純な周期点の回転ベクトルの組み合わせで作ることができ、周期点以外の点の回転ベクトルは周期点の回転ベクトルの組み合わせで近似できることから、回転集合は、単純な周期点に対応する回転ベクトルたちを頂点とした凸閉包で与えられることがわかる。グラフ上には単純な閉道は有限個しかないことから、単純な周期点も有限個しかなく、したがって、回転集合は実係数1次元ホモロジー群の凸多面体になることが分かる。この結果と記号力学系の性質から次のことが証明できる。 定理 ホモロジー自明な推移的同相写像(M,f)の回転集合Rot(f)は凸多面体であり、各頂点は周期点によって実現される。 Bowenは、公理A系の非遊走集合を有限個の基本集合に分割し、各基本集合上でマルコフ分割を構成した。一般に、遊走点の 極限集合は非遊走集合に含まれることを用いれば、以下の系が導かれる。 極限集合は非遊走集合に含まれることを用いれば、以下の系が導かれる。 系 ホモロジー自明な公理A系の回転集合Rot(f)は凸多面体の和集合である。 Thurstonは、擬アノソフ可微分同相写像に対してマルコフ分割を構成した。このことから、次の系が導かれる。 系 ホモロジー自明な擬アノソフ可微分同相写像の回転集合Rot(f)は凸多面体である。 |