学位論文要旨
| No | 113732 | |
| 著者(漢字) | 長山,雅晴 | |
| 著者(英字) | Nagayama,Masaharu | |
| 著者(カナ) | ナガヤマ,マサハル | |
| 標題(和) | 反応-拡散系に現れる解の衝突非消滅ダイナミクス | |
| 標題(洋) | Nonannihilation Dynamics of Solutions Arising in Reaction-Diffusion Systems | |
| 報告番号 | 113732 | |
| 報告番号 | 甲13732 | |
| 学位授与日 | 1998.03.30 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(数理科学) | |
| 学位記番号 | 博数理第98号 | |
| 研究科 | 数理科学研究科 | |
| 専攻 | ||
| 論文審査委員 | ||
| 内容要旨 | 神経繊維に見られる電位パルスの伝搬やBelousov-Zhabotinsky(BZ)化学反応に見られるリングパターンの理論的研究は反応拡散方程式系の考察から行われている.これらの基本モデルとして次の2成分系がある. fとgの典型的な例としては、神経電位の伝搬モデルとして使われるFitzHugh-Nagumo(FHN)タイプ を挙げることができる.ただし、0 これらのモデルに現れる典型的パターンとして、1次元では進行パルス、2次元ではリングパターンが挙げられる.これらのパターンの特徴は衝突消滅性である.この現象はBZ反応の実験にも観察されていたことから、2変数単安定興奮性反応拡散方程式系の進行パルスは衝突消滅することがこれまで信じられてきた. しかしながら、近年、方程式系(1),(2)とは異なった形の興奮性反応拡散方程式系において、進行パルスが必ずしも衝突消滅しないことが報告された.Petrov(1994)らは、3点平衡点を持つ自己触媒モデルに対して、また、Krisher,Mikhailov(1994)、Kawaguchi,Mimura(1997)はglobal coupling項を持つ実質3変数の方程式系(1),(2)に対して、1次元進行パルスの反射、2次元スポットパターンの反射が起こることを報告している. 以上のことから、必ずしも衝突消滅は興奮性反応拡散方程式系の進行パルスの特徴的な現象でないことがわかってきた.しかしながら、FHNモデルは衝突消滅性を持つことから、いかなるタイプの興奮性反応拡散方程式が衝突消滅するのか、あるいはしないのかは依然として問題となっていた. 本申請論文は以上の問題を考察することである.すなわち系(1)に対して (A-1)f(u, (A-2)(1)は安定進行パルス解を持つ. を満たす2成分反応拡散方程式系に対して次の問題を提起する. 仮定(A-1),(A-2)のもとで、果たして方程式系(1)は衝突非消滅現象を起こすか? この問題に対して、次の非線形項 を持つ1次発熱反応拡散方程式系(1)を考える.ここで、k(u)=exp(u/(1+u/c))である.ただし、(1)の変数u(t,x),v(t,x)はそれぞれ、時刻t場所xにおける温度と化学反応物質濃度に対応する.a,h, パラメータa,h,vc,c, (P-1)衝突非消滅現象の本質は何か? 本論文の目的は問題(P-1)に対して数値計算そして有限次元に縮約された系の解析から接近することである.論文の内容は(I)計算機支援による衝突非消滅現象の考察、(II)衝突非消滅現象の解析的考察、(III)数値実験による衝突非消滅性に起因する2次元パターンの考察、から成っている. ここでは数値実験から問題(P-1)を明らかにすることが目的である.最初に、(1),(3)に対して、衝突非消滅性を持つ進行パルス解の特徴を明らかにするために、安定進行パルス解や安定振動進行パルス解の存在範囲を調べた.その結果、安定な速度の遅い進行パルスの存在が数値計算より示唆された.何故速度の遅い進行パルス解が存在するのかを明らかにするために、定常パルス解の解構造と定常パルス解からの分岐を数値計算によって調べた.数値計算によって、定常パルス解からのsuper-critical分岐による速度の遅い進行パルス解の出現し、衝突非消滅現象が出現することが数値計算によって示唆された.この分岐によって現れた進行パルス解は、dが大きいことから、 側方抑制性とは次のことである:(1),(3)において、 そこで、この側方抑制性を持つ進行パルスが存在すれば反射するのかを考えた.(3)とは異なるタイプの非線形項を持つGray-Scottモデルにも、衝突非消滅現象が出現することが知られているので、速度の遅い進行パルスが存在するか否かを調べることにした.その結果、定常パルス解からのsuper-critical分岐よって、速度の遅い進行パルス解は出現すること、その進行パルスは反射することが数値計算によって示唆された.(図3)この進行パルスもまた、側方抑制性をもっていることがわかる. これらのことから、次を予想する. (C-1)反応拡散系のタイプによらず、もしも側方抑制性を持つ速度の遅い進行パルス解が存在するならば、衝突非消滅現象の性質を持つのではないだろうか? 以下では、側方抑制性を持つ速度の遅いパルスを単に速度の遅い進行パルスと呼ぶ. 予想(C-1)を解析的に論じるために速度の遅い進行パルス解が存在する系として、次の双安定FHN方程式を考える. ここでf(u)=u(1-u)(u-a).ただし、 系(4)において、非常に速度の遅い進行パルス解が存在し、その解は反射することが数値計算によって示された(図4).そこで、進行パルス解の反射を議論するために、パルスの位置を 次に、界面だけで記述できる方程式を導出するために、f(u)に対して区分線形f(u)=-u+H(u-a)を仮定する.ただし、H(x)=1,x>0, H(x)=0,x<0である.ここで、界面の速度が非常に遅いと仮定して、界面の時間変化を記述する4次元常微分方程式系を導出することができた.この系は、数値計算によって、図5と定性的に類似した界面の反射現象を示すことが確認された(図6).また、速度の遅い界面は幅が非常に広いことがわかる.そこで幅が非常に広い場合、すなわち こうして、この常微分方程式は速度の遅い進行パルス解の反射機構を理解するためのよい近似になっていることが示唆された.しかし、この正当化と界面反射の厳密な証明は今後に残された課題である. 最後に、衝突非消滅現象に起因して出現する2次元時間空間パターンについて考察する.ここでは、(1),(3)に現れる複雑な2次元パターンの生成機構の本質は何であるかを数値計算によって考察した.最初に、プラナー進行パルスの安定性を調べた.その結果、速度の遅い進行パルスが存在するとき、プラナー進行パルスは不安定であることが示唆された.この結果が一般に成り立つかどうかを検証するために、Gray-Scottモデルに対して、プラナー進行パルスの性質を調べた結果、予想したように速度の遅い進行パルスはプラナー不安定であることが示唆された.この事実から、一般的に速度の遅い進行パルスは、衝突非消滅性だけでなくプラナー不安定性も持っていることが示唆された.そして、(1),(3)とGray-Scottモデルでは、このような状況下でのリングパターンは衝突非消滅性とプラナー不安定性によって崩壊し、複雑なパターンを生成することが示唆された.以上の結果は、反応拡散系のタイプによらず、もし速度の遅い進行パルスが存在するならば、2次元では複雑なパターンを生成するのではないか?という期待を抱かせる. | |
| 審査要旨 | 本論文提出者は非線形散逸系の一つのとしての反応拡散方程式を取り上げ,そこに現れるパルス進行波の衝突ダイナミクスを論じている.これまで非線形散逸系に現れる進行パルス波や拡大するリング波は衝突消滅することが実験及びそのモデル系から示唆されてきたが,最近,非線形散逸系でありながら,必ずしも衝突消滅するものではないパルス進行波が存在することが報告されている.本論文ではこのような衝突非消滅現象の本質は何であるかという問題を提起している.得られた結果は,2成分反応拡散方程式においては非常に対称性が高く,速度が非常に遅いパルス進行波には衝突反射する現象が普遍的に起こることを数値シミュレーションから示唆したことである.更に,この結果を理論的に示すために,速度が非常に遅いパルス進行波が存在する2成分双安定反応拡散系を取り上げ,その1次元系に対して,パルスの運動を界面の運動として捉える界面ダイナミクス法から1次元自由境界問題を導出し、更に,この問題に対して速度が非常に遅いという仮定をおくことから,界面だけの4次元常微分方程式を導出したのである.この導出は形式的なものであるが,解析及びそれを相補する数値解析によって,速度の非常に遅いパルス進行波の相互作用を記述する最も単純な系であることが示唆された.本論文での成果は,前半は数値シミュレーションにより,パルスダイナミクスにおける一つの普遍性を見つけたことであり,後半はそれを理論的に説明するために,縮約系を導出したことである.これらの結果はパルスダイナミクスの機構解明において一つの展開を与えるものである. 以上の理由から、本論文での成果はパターンダイナミクスに対して応用解析学の視点から新たな光をあてるものであり、そこで用いられた方法は数理科学的方法論の一つの方向性を示唆するものと考えられる。 よって論文提出者長山雅晴氏は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/54664 |


 )=0は3次関数的非線形項とし,g(u,
)=0は3次関数的非線形項とし,g(u, に対して、興奮性を持つ.
に対して、興奮性を持つ.
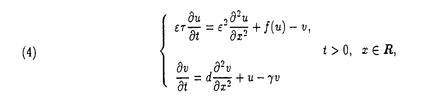
 ,d,a,
,d,a, は正定数,
は正定数, 1(t)>
1(t)>




