| 内容要旨 | | この論文ではd次元格子Zd上のspeed changeのある排他過程(exclusion process)の流体力学極限の問題を、非対称で、いわゆる勾配条件(gradient condition)を満たさない非勾配型のモデルへと拡張して考える。 d次元離散トーラス N=(Z/NZ)d上のspeed changeのある排他過程とは、配置空間 N=(Z/NZ)d上のspeed changeのある排他過程とは、配置空間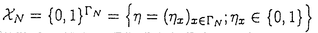 上のMarkov過程で、次の作用素LNによって生成されるものである。 上のMarkov過程で、次の作用素LNによって生成されるものである。  ここでcはZd×Zd× 上の非負関数で、jump rateを与える。但し、 上の非負関数で、jump rateを与える。但し、 で、 で、 Nの元は周期的に拡張することで Nの元は周期的に拡張することで の元とみなす。また、 の元とみなす。また、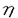 xyは xyは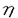 のx座標とy座標を入れ換えたものである。次に、無限粒子系であるZd上のspeed changeのある排他過程とは、 のx座標とy座標を入れ換えたものである。次に、無限粒子系であるZd上のspeed changeのある排他過程とは、 上のMarkov過程で、次の作用素Lによって生成されるものである。 上のMarkov過程で、次の作用素Lによって生成されるものである。  ここで、F0はX上の局所関数全体(有限個の座標にしか依らない関数全体)を表す。 この論文では、(1)に対応する系に対して拡散型スケール変換を施し、N→∞として得られる極限の粒子密度の特徴付けを行う事を目標とする。このような排他過程に関する流体力学極限の問題は、対称な非勾配系に対しては[1]で、非対称な場合では、speed changeのない単純排他過程(simple exclusion process)について[4]で論じられている。ここでは、非対称、非勾配なspeed changeのある場合で、しかも、対応する対称過程も非勾配であるようなものへと一般化する。 ここで扱うモデルは以下の条件を満たすものとする。 (a)c(x,y,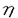 )は局所関数で、 )は局所関数で、 . . (b)cは平行移動不変、つまり  但し、 xはX上のシフト作用素で( xはX上のシフト作用素で( x x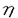 )u= )u=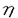 u+x. u+x. (c)Bernoulli測度 は不変測度。 は不変測度。 (d)各粒子のjumpの平均は0、つまり 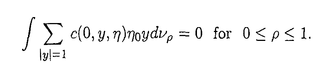 (e)Lは次のstrong sector conditionとよばれる条件を満たす:任意の に対し に対し  (f)拡散行列 は滑らか、つまりa( は滑らか、つまりa( )∈C2([0,1]). )∈C2([0,1]). 但し、a( )は次のように与えられる: )は次のように与えられる:  (K)=[-K,K]d∩Zdとし、 (K)=[-K,K]d∩Zdとし、 上の関数f=f( 上の関数f=f( )に作用する作用素 )に作用する作用素 を次で定義する。 を次で定義する。 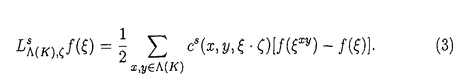 但し、cS(x,y,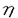 )=1/2{c(x,y, )=1/2{c(x,y,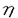 )+c(x,y, )+c(x,y,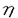 xy)}で、 xy)}で、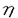 ∈Xは ∈Xは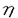 = = ・ ・ , , , , と分解されているものとする。ここで次の関数空間を考える。 と分解されているものとする。ここで次の関数空間を考える。  但し、 は は 上の一様確率測度による期待値を、s(g)はgのsupportのsizeを表す。また、| 上の一様確率測度による期待値を、s(g)はgのsupportのsizeを表す。また、| (K)|=(2K+1)dである。この関数空間 (K)|=(2K+1)dである。この関数空間 の元gに対し, の元gに対し,  とおく。このとき、 によらずに によらずに  が存在する。ここで、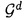 に属する次の関数を考える。 に属する次の関数を考える。  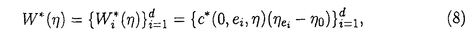  但し、eiは第i座標1の単位ベクトルを表し、c*(x,y,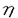 )=c(x,y, )=c(x,y, xy)である。 xy)である。 はgradient、W*はcurrentとよばれる関数である。このとき、次の補題が成立する。 はgradient、W*はcurrentとよばれる関数である。このとき、次の補題が成立する。 補題1 (a)-(e)をみたすモデルに対し、各 ごとに次の関係式をみたす唯一のd次正方行列a( ごとに次の関係式をみたす唯一のd次正方行列a( )が存在する: )が存在する: 任意のl∈Rdに対し、  但し、(,)はRdでの内積を表す。 この補題1に現れるd次正方行列a( )で拡散行列を定義する。 )で拡散行列を定義する。 さて、これら(a)-(f)を満たすモデルに対して、N2LNが生成するXN上のMarkov過程を とし、その質量分布(empirical-mass distribution)を とし、その質量分布(empirical-mass distribution)を 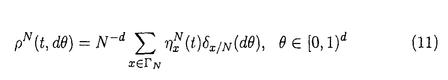 で定義する。 ここで次の非線形拡散方程式を考える:  この論文の主定理は、次の定理である。 定理1 (12)が初期値 0( 0( )∈(0,1)に対し滑らかな解 )∈(0,1)に対し滑らかな解 (t, (t, )を持ち、 )を持ち、 とする。このとき、∀t>0に対し とする。このとき、∀t>0に対し 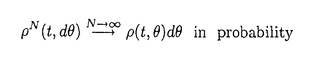 が成り立つ。 但し、 は は 0( 0( )に対応する局所平衡状態を,f0は )に対応する局所平衡状態を,f0は N(0)のXN上の分布のXN上の一様確率測度 N(0)のXN上の分布のXN上の一様確率測度 Nに対する密度を、 Nに対する密度を、 は相対エントロピーを表す。 は相対エントロピーを表す。 我々はこの定理を、Yauが[5]で用いた相対エントロピー法を使って証明する。相対エントロピー法では、局所平衡状態に対する相対エントロピーを計算するが、非勾配型のモデルに対しては、局所平衡状態の第二次近似 t( t(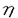 )d )d Nまで考えなくてはなるない事が知られている([1])。ここで、 Nまで考えなくてはなるない事が知られている([1])。ここで、  但し、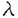 (t, (t, )=log{ )=log{ (t, (t, )/(1- )/(1- (t, (t, ))}で ))}で (t, (t, )は(12)の解、Fは )は(12)の解、Fは の元、Ztは規格化定数である。この時、考える相対エントロピーは次で表される。 の元、Ztは規格化定数である。この時、考える相対エントロピーは次で表される。  ここで、ftは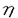 N(t)のXN上の分布の密度関数である。相対エントロピー法によれば、大偏差原理型の評価やエントロピー不等式等を用いる事で、定理1は次の補題から得られる事が分かる。 N(t)のXN上の分布の密度関数である。相対エントロピー法によれば、大偏差原理型の評価やエントロピー不等式等を用いる事で、定理1は次の補題から得られる事が分かる。 補題2 任意の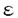 >0に対し、あるF∈ >0に対し、あるF∈ が存在して、 が存在して、  とできる。 補題2を示す時に、非対称な項の取扱いが問題になるが、strong sector condition(e)を使って、次の評価が得られる。 補題3 任意の0 と任意の局所関数fに対して、 と任意の局所関数fに対して、  ここで、Csは条件(e)で与えられた定数。 この論文では、この補題3を用いて、非対称な項を対称な項でcontrolするという議論を行う。 参考文献[1]T.Funaki,K.Uchiyama and H.T.Yau:Hydrodynamic limit for lattice gas reversible under Bernoulli measures,in:Nonlinear Stochastic PDE’s:Hydrodynamic Limit and Burger’s Turbulence(eds.Funaki and Woyczynski),IMA volume77(1995),1-40.[2]H.Spohn:Large Scale Dynamics of Interacting Particles,Springer,1991.[3]S.R.S.Varadhan:Nonlinear diffusion limit for a system with nearest neighbor interactions-II,in:Asymptotic Problems in Probability Theory:Stochastic Models and Diffusions on Fractals(eds.Elworthy and Ikeda),Longman,1993,75-128.[4]L.Xu:Diffusive scaling limit for mean zero asymmetric simple exclusion processes,Courant thesis,1993.[5]H.T.Yau:Relative entropy and hydrodynamics of Ginzburg-Landau models,Letters Math.Phys.,22(1991),63-80. |