| 内容要旨 | | 4次元球面S4または4次元空間 に埋め込まれた曲面についてさまざまな方法で研究されている。曲面を に埋め込まれた曲面についてさまざまな方法で研究されている。曲面を へ射影しその像から研究する方法ではCarter氏と斉藤氏[CS]やRoseman氏[R]により曲面結び目版Reidemeister moveなどが求められている。また矢島氏[Y1]などによりknotted2-sphereで2重点のみもつものについて研究されている。曲面から第4座標への写像がMorse関数になるようにし、 へ射影しその像から研究する方法ではCarter氏と斉藤氏[CS]やRoseman氏[R]により曲面結び目版Reidemeister moveなどが求められている。また矢島氏[Y1]などによりknotted2-sphereで2重点のみもつものについて研究されている。曲面から第4座標への写像がMorse関数になるようにし、 での切り口から研究する方法がある。鎌田氏[K]により曲面結び目版braidが研究され、吉川克之氏[Y2]により での切り口から研究する方法がある。鎌田氏[K]により曲面結び目版braidが研究され、吉川克之氏[Y2]により の切り口(classical knot)にある情報を加えたものがknotted surfaceの表示になることが示されそのうち交点数の少ないものについて調べられた。著者はR3への射影を使い、4次元空間に埋め込められたトーラスについて研究した。 の切り口(classical knot)にある情報を加えたものがknotted surfaceの表示になることが示されそのうち交点数の少ないものについて調べられた。著者はR3への射影を使い、4次元空間に埋め込められたトーラスについて研究した。 pを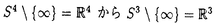 への射影、FをS4に埋め込まれたsurfaceとし、 への射影、FをS4に埋め込まれたsurfaceとし、 (F*)=cl{x∈p(F)|p-1(x)∩Fは2点以上}、 (F*)=cl{x∈p(F)|p-1(x)∩Fは2点以上}、 (F)=p-1( (F)=p-1( (F*))∩Fとおく。 (F*))∩Fとおく。 1.本論文の内容第I論文 題目Knotted tori whose singular set consists of three disjoint double curves(singular setが互いに交わらない3本の単純閉曲線からなるknotted torusについて)  内に埋め込まれたS1すなわちclassical knot について、交点数の少ないものについてよく調べられている。また相曽氏[A]はR4に埋め込まれた2-sphereでその射影のsingular setが交わりのない5本以下の単純閉曲線からなるものについて分類した。著者は以前の論文でS4に埋め込まれたtorusでその射影のsingular setが互いに交わらない2本以下の単純閉曲線からなるものは自明であることを示した。(すなわちS4内のあるsolid toursの境界になる。) 内に埋め込まれたS1すなわちclassical knot について、交点数の少ないものについてよく調べられている。また相曽氏[A]はR4に埋め込まれた2-sphereでその射影のsingular setが交わりのない5本以下の単純閉曲線からなるものについて分類した。著者は以前の論文でS4に埋め込まれたtorusでその射影のsingular setが互いに交わらない2本以下の単純閉曲線からなるものは自明であることを示した。(すなわちS4内のあるsolid toursの境界になる。) 論文Iでは次の定理を示した。 Theorem.S4に埋め込まれたtorus Tでその射影のsingular set (T*)が3本の交わらない単純閉曲線からなる時、torusをambient isotopyで動かし自明なtorus、trefoil knotのspun torus、trefoil knotのtwist spun torusかまたはtrefoil knotのspun 2-sphereに1-handleをつけて得られたtorusになる。 (T*)が3本の交わらない単純閉曲線からなる時、torusをambient isotopyで動かし自明なtorus、trefoil knotのspun torus、trefoil knotのtwist spun torusかまたはtrefoil knotのspun 2-sphereに1-handleをつけて得られたtorusになる。 さらに自明なtorus、trefoil knotのspun torus、trefoil knotのtwist spun torusとtrefoil knotのspun 2-sphereに1-handleをつけて得られたtorusは互いにambient isotopyではうつり合えない事もわかった。torusの向きが2通り選べるがそれらは互いにambientisotopyうつり合う事もわかった。また、trefoil knotのtwist spun torusはribbon torusにはambient isotopyでうつり合えない事もわかった。 注意として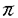 1(S4\{trefoil knotのspun tours})と 1(S4\{trefoil knotのspun tours})と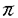 1(S4\{trefoil knotのtwist spun torus})と 1(S4\{trefoil knotのtwist spun torus})と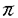 1(S4\{trefoil knotのspun 2-sphereに1-handleを付けて得られたtorus})は 1(S4\{trefoil knotのspun 2-sphereに1-handleを付けて得られたtorus})は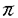 1(S3\{trefoil knot})に同型である。 1(S3\{trefoil knot})に同型である。 寺垣内氏により定義されたsymmetry-spun torusを紹介する。 :B3→B3をZ軸を中心に :B3→B3をZ軸を中心に 回転するmap、S4=∂B5=∂B3×B2∪B3×∂B2とする。S4内のknotted torus Fがsymmetry-spun torusとは整数aとbとB3内のlink Kbが存在し次の3つの条件を満たす。 回転するmap、S4=∂B5=∂B3×B2∪B3×∂B2とする。S4内のknotted torus Fがsymmetry-spun torusとは整数aとbとB3内のlink Kbが存在し次の3つの条件を満たす。 (1)KbとZ軸は交わらない (2) (3) 但しb≠0かつ∂B2は[0,2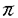 ]/0〜2 ]/0〜2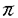 と同一視する。このFをTa(Kb)で表す。K1をB3内のknotとする。sptun toursとはT0(K1)で、twist spun toursとはT1(K1)の事である。 と同一視する。このFをTa(Kb)で表す。K1をB3内のknotとする。sptun toursとはT0(K1)で、twist spun toursとはT1(K1)の事である。 spun 2-sphereに1-handleを付けて得られたtorusの定義は次の通りである。 、Kを 、Kを 内のknotとする。 内のknotとする。 と置く。SをKから得られたspun 2-sphereという。 と置く。SをKから得られたspun 2-sphereという。 をS3内のarcでp(S)∩ をS3内のarcでp(S)∩ =∂ =∂ 、∂ 、∂ はp(S)\ はp(S)\ (S*)の同じ成分に含まれるとする。ここで (S*)の同じ成分に含まれるとする。ここで (S*)はSの (S*)はSの への射影のsingular setである。このとき への射影のsingular setである。このとき に沿ってSに1-handleを付けて得られたtorusをspun 2-sphereに1-handleを付けて得られたtorusという。 に沿ってSに1-handleを付けて得られたtorusをspun 2-sphereに1-handleを付けて得られたtorusという。 第II論文 題目Knotted tori with only double points (2重点のみもつknotted torusについて) 矢島氏により次のことが示された。Fをknotted 2-sphereでその射影のsingular setが2重点のみからなるとする。このときFはribbon 2-knotにambient isotopicである。論文IIではこの定理をtorusの場合に拡張した。つまり次のことを示した。 Theorem.Fをknotted torusでその射影のsingular set  (F*)が2重点とbranch pointのみからなるとする。このときFはribbon torusまたはsymmetry-spun toursからm-fusionして得られたtorusにambient isotopicである。 (F*)が2重点とbranch pointのみからなるとする。このときFはribbon torusまたはsymmetry-spun toursからm-fusionして得られたtorusにambient isotopicである。 Fを 内の向きの付いたknotted surfaceとする。 内の向きの付いたknotted surfaceとする。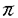 1(R4\F)がZに同型ならばFは自明であるかという問題がある。この問題の答えはtopological categoryについては球面の場合にFreedman氏により正しい事が示された。PL categoryまたはsmooth categoryにおいては一般には解かれていない。丸本氏[M]により1-fusion ribbon 2-knotの場合に、寺垣内氏[T]によりsymmetry-spun toursの場合に、Scharlemann氏[S]により2-sphereでcritical pointsが4つの場合に正しいことが示されている。寺垣内氏の結果と著者のtorusの場合の結果を合わせることにより次の結果を得た。 1(R4\F)がZに同型ならばFは自明であるかという問題がある。この問題の答えはtopological categoryについては球面の場合にFreedman氏により正しい事が示された。PL categoryまたはsmooth categoryにおいては一般には解かれていない。丸本氏[M]により1-fusion ribbon 2-knotの場合に、寺垣内氏[T]によりsymmetry-spun toursの場合に、Scharlemann氏[S]により2-sphereでcritical pointsが4つの場合に正しいことが示されている。寺垣内氏の結果と著者のtorusの場合の結果を合わせることにより次の結果を得た。 Corollary.FをS4内のknotted torusとする。その射影のsingular set  (F*)が2重点のみからなるとする。F上でのsingular set (F*)が2重点のみからなるとする。F上でのsingular set  (F)のすべでの成分はF内でhomotopiczeroでないとする(つまりF内で円板の境界とならない単純閉曲線である)。この時、もし (F)のすべでの成分はF内でhomotopiczeroでないとする(つまりF内で円板の境界とならない単純閉曲線である)。この時、もし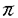 1(S4\F)がZに同型ならばFは自明である。 1(S4\F)がZに同型ならばFは自明である。 Gを 内のknotted surfaceとする。R4内のknotted surface FがGからm-fusionして得られたsurfaceとはある埋め込みhj:B2×I→R4が存在し(j=1,2,…,m)次の3つの条件を満たす 内のknotted surfaceとする。R4内のknotted surface FがGからm-fusionして得られたsurfaceとはある埋め込みhj:B2×I→R4が存在し(j=1,2,…,m)次の3つの条件を満たす (1)hi(B2×I)∩hj(B2×I)=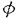 (i≠j) (i≠j) (2)全てのjに対しhj(B2×I)∩G=hj(B2×{0,1}) (3)F=(G\∪hj(B2×{0,1}))∪(∪hj(∂B2×I)) 特にGがtrivial 2-link(いくつかのS2からなりambient isotopyで ×{0}内の互いに交わらないS2達に出来る)の時、Fをribbon surfaceという。さらにribbon surface FがS2の時、Fをribbon 2-knotという。 ×{0}内の互いに交わらないS2達に出来る)の時、Fをribbon surfaceという。さらにribbon surface FがS2の時、Fをribbon 2-knotという。 2.参考論文題目An unknotting theorem for tori in S4 (Rev.Mat.Univ.Complut.Madrid掲載予定) S4に埋め込まれたtorusでその射影のsingular setが互いに交わらない1本の単純閉曲線からなるものは自明であることを示した。(すなわちS4内のあるsolid toursの境界になる。) 題目An unknotting theorem for tori in S4 II (Kobe J.Math.13(1996)掲載) S4に埋め込まれたtorusでその射影のsingular setが互いに交わらない2本以下の単純閉曲線からなるものは自明であることを示した。 題目Immersions from the 2-sphere to the 3-sphere with only two triple points immersionを研究することは3重点をもつknotted surfaceを研究することともつながる。Banchoff氏[B]により次のことが示された。Fをclosed surface、fをFからS3へのimmersionとする。このときfの3重点の数はFのEuler標数とmodulo 2で等しい。つまりimmersed 2-sphereの中で3重点をもつもの内で1番簡単なものは3重点を2コもつものである。この論文ではimmersed 2-sphereで3重点をちょうど2コもつものについて調べた。 Theorem.fをS2からS3へのimmersionとする。Cをsingular set S(f)の成分で3重点を高々2コもつもの、NをS3におけるCのregular neighborhoodとする。このとき(N,N∩f(S2))の場合は6通りある。 実際にこの論文で具体的に6通りの例を構成した。 題目On singular sets of immersions of closed surfaces into 3-manifolds fをoriented closed surfaceからoriented 3-manfold へのimmersionとする。Cをsingular set S(f)の成分とする。このときCの3重点の数は偶数個である事を示した。 謝辞 この博士論文制作に際しての松本幸夫先生のご指導、ご助言に心より感謝いたします。論文"On simply knotted tori in S4"のレフェリー方には丁寧に論文を読み多くの意見をいただき感謝いたします。 また著者の研究の援助をしてくださった風樹会、学術振興会のみなさまにも御礼申し上げます。 REFERENCES[A] H.Aiso,Crossing circleが5本以下であるsimply knotted sphereの分類について,Master thesis,The University of Tokyo,昭和59年度.[B] T.Banchoff,Triple points and singularities of projections of smoothly immersed surfaces,Proc.Amer.Math.Soc.46(1974),402-406.[CS]S.Carter and M.Saito,Reidemeister Moves for Surface Isotopies and Their Interpretation As Moves to Movies,J.Knot Theory Ramifications 2(1993),251-284.[F] Freedman,M.H.,The topology of four-dimensional manifolds,J.Differential Geom.17(1982),357-435.[K] S.Kamada,On2-dimensional braids and 2-links,In:The 3rd korea-Japan school of knots and links(Teajon 1994),Proc.Applied Math.four,Bull.Amer.Math.Soc.,33-39.[M] Y.Marumoto,On ribbon 2-knots of 1-Fusion,Math.Sem.Notes,Kobe Univ.5(1977),59-68.[R] D.Roseman,Reidemeister-Type Moves for Surfaces in Four Dimensional Space,preprint.[S] M.Scharlemann,Smooth spheres in P4 with four crtical points are standard,Invent.Math.79(1985),125-141.[T] M.Teragaito,Symmetry-spun tori in the four-sphere,Proceedings of Knots 90,163-171.[Y1]T.Yajima,On simply knotted spheres in R4,Osaka J.Math.1(1964),133-152.[Y2]K.Yoshikawa,An enumeration of surfaces in four-space,Osaka J.Math.31(1994),497-522. |
| 審査要旨 | | 古典的な結び目理論の研究対象は,3次元球面S3のなかの円周S1である。E.Artin[1925]は,3次元上半空間内の結ばれた線分を,その線分の両端がのっている2次元平面(z=0)を「軸」として回転させ,4次元球面S4のなかの結ばれた2次元球面S2を構成した。これをspun 2-knotという。これによって,4次元の結び目理論が成立した。以来,4次元の結び目理論は多くの研究者によって研究されてきたが,いまだに,多くの未解決問題を含む若い分野であると考えられる。 古典的な結び目理論と異なり,4次元の結び目理論では,球面ばかりでなく,種数をもつ閉曲面の「結び目」も考えることができる。 論文提出者の志摩亜希子氏は,4次元球面S4のなかのトーラスT2の結び目を研究した。その方法は,自然な射影p:S4\{∞}→S3\{∞}により,S4内に埋め込まれたトーラスT2を3次元球面内に落として,その自己交叉の様子を調べることである。論文は2部に分かれており,第1部の主定理は次のように述べられる。 定理1S4に埋め込まれたトーラスT2の3次元球面S3内への射影像p(T2)の自己交叉が2重点のみからなり,しかも,それらが互いに交わらない3本の単純閉曲線からなるならば,はじめのトーラスT2はS4のイソトピーで次の4つのトーラスのどれかに移せる。しかも,これら4つのトーラスは互いにイソトピーでは移り合わない。 (1)自明なトーラス (2)3葉結び目から作られたspun torus (3)3葉結び目から作られたtwist spun torus (4)3葉結び目から作られたArtinのspun 2-knotに自明なハンドルをつけたトーラス。 なお,射影像p(T2)の自己交叉が2本以下の単純閉曲線からなる場合は,論文提出者により,参考論文のなかで既に解決されており,それらは自明なトーラスにイソトピーで移せるということが証明されている。 定理1の証明は,射影像p(T2)の3本の自己交叉線の引き戻しであるような6本の円周のT2内での配置を全部で157通りに分類し,各々の配置に対応するT2の結ばれ方について考察してゆくものである。この証明法には,論文提出者の並々ならぬ数学的力量が感じられる。 第2部の主定理は次のように述べられる。 定理2S4に埋め込まれたトーラスT2の3次元球面S3内への射影像p(T2)の自己交叉が2重点のみからなるならば,それは,自明に埋め込まれた2次元球面の非交和からfusionという操作で得られたトーラスであるか,または寺垣内氏の定義したsymmetry-spun torusからfusion操作によって得られたトーラスである。 系定理2の仮定にさらに,射影像の自己交叉線の引き戻しの各成分がH1(T2)のなかで0でないという仮定を付け加える。このとき,もし基本群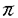 1(S4-T2)が 1(S4-T2)が に同型であれば,はじめのトーラスT2は自明である。 に同型であれば,はじめのトーラスT2は自明である。 以上の諸結果は4次元の結び目理論に興味深い知見を付け加え,この分野の発展に大いに寄与するものである。 よって,論文提出者志摩亜希子氏は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認められる。 |