以下にこの論文「Sp(2,R)上のフーリエ・ヤコビ型球関数」の要旨を述べる。 まず最初に、問題とその背景を説明する。保型形式の各種のフーリエ展開は、L関数などを研究する手段として最も基本的なもののひとつである。これは特に有界対称領域上の正則な保型形式については、今までに具体的にいろいろ調べられている。その一方で、正則でない多変数保型形式は、不連続群のコホモロジー群に関連して、調和的なものが松島・村上理論などで自然に現れる。ところが、これらの保型形式はその重要性にもかかわらず、「フーリエ展開」という基本的主題についてさえ、実質的にはほとんど何も調べられていない。このような保型形式のフーリエ展開に現れる特殊関数が、我々の関心である。 そこで、問題を一般的な形で提示する。Gを実簡約可能群、KをGの極大コンパクト部分群とする。さらに、HをGの部分群とし、 をHの既約ユニタリ表現とする。このときGの既約ユニタリ表現 をHの既約ユニタリ表現とする。このときGの既約ユニタリ表現 に対して、次の(gc,K)加群としての絡空間 に対して、次の(gc,K)加群としての絡空間 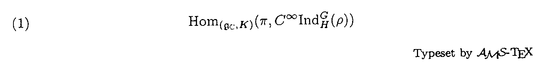 を考える。ここに、gcはGのリー環gの複素化を表わし、C∞IndはHからGへのC∞-誘導表現を表わす。この絡空間は、G、Hおよび の適当な組み合わせに対して、保型形式論にとって重要な考察対象になることが知られている。とりわけ、HとしてGの標準的な極大べき単部分群Nm、 の適当な組み合わせに対して、保型形式論にとって重要な考察対象になることが知られている。とりわけ、HとしてGの標準的な極大べき単部分群Nm、 としてNmの非退化指標をとるとき、誘導表現 としてNmの非退化指標をとるとき、誘導表現 はゲルファント・グラーエフ表現と呼ばれ、この絡空間は保型形式論および表現論の双方の立場から多くの研究がされてきた。また、この絡空間の中で特にその動径成分上緩増加である関数より成るゲルファント・グラーエフ表現の表現空間の部分空間に値をとるものは はゲルファント・グラーエフ表現と呼ばれ、この絡空間は保型形式論および表現論の双方の立場から多くの研究がされてきた。また、この絡空間の中で特にその動径成分上緩増加である関数より成るゲルファント・グラーエフ表現の表現空間の部分空間に値をとるものは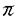 のホイッタカー模型として知られ、G上の保型形式のフーリエ展開やL関数と密接な関係を持つ。このとき、ホイッタカー模型の重複度(すなわちこの絡空間の次元)、および明示的な表示がその研究の中心的な興味である。(1)においてHをNmよりも小さいべき単部分群Nとし、 のホイッタカー模型として知られ、G上の保型形式のフーリエ展開やL関数と密接な関係を持つ。このとき、ホイッタカー模型の重複度(すなわちこの絡空間の次元)、および明示的な表示がその研究の中心的な興味である。(1)においてHをNmよりも小さいべき単部分群Nとし、 をNの既約ユニタリ表現とするとき、誘導表現 をNの既約ユニタリ表現とするとき、誘導表現 は一般ゲルファント・グラーエフ表現と呼ばれる。保型形式のフーリエ展開を考察する際、 は一般ゲルファント・グラーエフ表現と呼ばれる。保型形式のフーリエ展開を考察する際、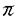 の一般ゲルファント・グラーエフ表現への埋め込み、特にNに対する の一般ゲルファント・グラーエフ表現への埋め込み、特にNに対する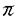 のホイッタカー模型の適当な一般化を考える必要がしばしば生ずるが、この場合の絡空間(1)は一般に無限次元になる。そこで我々は、絡空間(1)が有限次元となるようなNを含む適当な部分群Rに対する「一般化されたホイッタカー模型」を考察する。 のホイッタカー模型の適当な一般化を考える必要がしばしば生ずるが、この場合の絡空間(1)は一般に無限次元になる。そこで我々は、絡空間(1)が有限次元となるようなNを含む適当な部分群Rに対する「一般化されたホイッタカー模型」を考察する。 次に、この論文における問題の定式化、および主結果について説明する。まず、次数2の実シンプレクティック群Sp(2,R)上の保型形式と関係したある種の球関数を以下のように定義する。G=Sp(2,R)とし、Gの極大コンパクト部分群をK U(2)とする。さらにPJをGのヤコビ極大放物部分群とし、MJAJNJをPJのラングランヅ分解とする。 U(2)とする。さらにPJをGのヤコビ極大放物部分群とし、MJAJNJをPJのラングランヅ分解とする。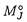 をMJの単位元連結成分とするとき、 をMJの単位元連結成分とするとき、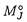 とNJの半直積群を とNJの半直積群を とおく。ここで、PJのべき単根基NJは3次元ハイゼンベルク群H3と同型で、その中心はRと同型であることに注意する。また、PJのレビ部分MJAJはNJに共役によって作用するが、MJはこの作用に関するNJの中心の中心化群であり、 とおく。ここで、PJのべき単根基NJは3次元ハイゼンベルク群H3と同型で、その中心はRと同型であることに注意する。また、PJのレビ部分MJAJはNJに共役によって作用するが、MJはこの作用に関するNJの中心の中心化群であり、 。よって、RJはヤコビ群 。よって、RJはヤコビ群 と同型になる。そこで、中心指標が自明でないRJの既約ユニタリ表現 と同型になる。そこで、中心指標が自明でないRJの既約ユニタリ表現 とGの既約ユニタリ表現 とGの既約ユニタリ表現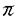 に対し、(gc,K)加群としての絡空間(1)、すなわちRJに対する一般化された代数的ホイッタカー汎関数の空間 に対し、(gc,K)加群としての絡空間(1)、すなわちRJに対する一般化された代数的ホイッタカー汎関数の空間 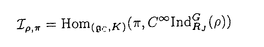 を考える。さて、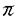 のK-type のK-type 、 、 *は *は の反傾表現、に対し、i: の反傾表現、に対し、i: *→ *→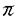 |KをK-同変写像とするとき、写像 |KをK-同変写像とするとき、写像  によって絡空間 の元Tの の元Tの *への制限 *への制限 を定義する。ここに、i*はiの引き戻し、 を定義する。ここに、i*はiの引き戻し、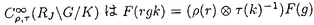 ,(r,g,k)∈RJ×G×KをみたすC∞関数 ,(r,g,k)∈RJ×G×KをみたすC∞関数 の空間とする。この写像によって、絡空間 の空間とする。この写像によって、絡空間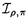 をG上の球関数として捉える。とくに、 をG上の球関数として捉える。とくに、 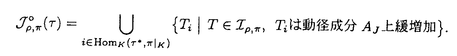 とおき、 の元を( の元を( , ,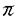 ; ; )型のフーリエ・ヤコビ型球関数と定義する。このフーリエ・ヤコビ型球関数は、 )型のフーリエ・ヤコビ型球関数と定義する。このフーリエ・ヤコビ型球関数は、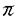 としてGの正則離散系列表現をとったとき、正則ジーゲル保型形式のフーリエ・ヤコビ展開の係数に現れる関数である。 としてGの正則離散系列表現をとったとき、正則ジーゲル保型形式のフーリエ・ヤコビ展開の係数に現れる関数である。 上で定義したフーリエ・ヤコビ型球関数について、その重複度、および明示公式に興味がある。この論文では、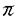 として次に挙げるGの既約ユニタリ表現を扱った。ひとつはPJ-主系列表現、つまりヤコビ極大放物部分群PJから誘導された一般主系列表現、もうひとつは離散系列表現、つまり正則(反正則)離散系列表現と「大きな」離散系列表現。このとき次の結果を得た。 として次に挙げるGの既約ユニタリ表現を扱った。ひとつはPJ-主系列表現、つまりヤコビ極大放物部分群PJから誘導された一般主系列表現、もうひとつは離散系列表現、つまり正則(反正則)離散系列表現と「大きな」離散系列表現。このとき次の結果を得た。 主定理.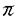 をGのPJ主系列(または離散系列)表現、 をGのPJ主系列(または離散系列)表現、 *を *を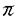 のコーナー(または極小)K-typeとする。このとき、中心指標が自明でないRJの各既約ユニタリ表現 のコーナー(または極小)K-typeとする。このとき、中心指標が自明でないRJの各既約ユニタリ表現 に対し、( に対し、( , ,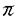 ; ; )型のフーリエ・ヤコビ球関数の空間 )型のフーリエ・ヤコビ球関数の空間 は は 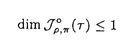 をみたす。また、この球関数は動径成分AJ上の関数として、メイジャーのG関数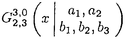 、もしくはより「退化した」関数によって表示される。 、もしくはより「退化した」関数によって表示される。 ここで、メイジャーのG関数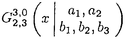 はメリン・バーンズ型の積分によって定義される多価関数で、一般化された超幾何級数2F2(x)による表示を持ち、合流型の3階の常微分方程式をみたしている。また、特別なパラメータai、bjの値に対しては古典的なホイッタカー関数 はメリン・バーンズ型の積分によって定義される多価関数で、一般化された超幾何級数2F2(x)による表示を持ち、合流型の3階の常微分方程式をみたしている。また、特別なパラメータai、bjの値に対しては古典的なホイッタカー関数 、 、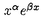 の形の関数などに(特殊関数として)「退化」する。特に の形の関数などに(特殊関数として)「退化」する。特に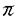 が正則離散系列表現のとき、フーリエ・ヤコビ型球関数は が正則離散系列表現のとき、フーリエ・ヤコビ型球関数は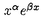 の形の関数で表わされ、古典的に知られたものと一致する。 の形の関数で表わされ、古典的に知られたものと一致する。 この定理は、( , ,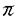 ; ; )型のフーリエ・ヤコビ型球関数をその値の空間 )型のフーリエ・ヤコビ型球関数をその値の空間 の適当な基底によって展開したとき、その係数のみたす差分微分方程式系を明示的に書き下し、実際に解くことによって示される。この差分微分方程式系は、シュミット作用素と呼ばれる1階の共変微分作用素を適当に組み合わせることによって得られる。特に、離散系列表現 の適当な基底によって展開したとき、その係数のみたす差分微分方程式系を明示的に書き下し、実際に解くことによって示される。この差分微分方程式系は、シュミット作用素と呼ばれる1階の共変微分作用素を適当に組み合わせることによって得られる。特に、離散系列表現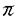 に対しては、絡空間(1)のシュミット作用素による特徴づけが山下博氏によって知られている(1990)。また、中心指標が自明でないRJの既約ユニタリ表現 に対しては、絡空間(1)のシュミット作用素による特徴づけが山下博氏によって知られている(1990)。また、中心指標が自明でないRJの既約ユニタリ表現 は、ヤコビ群のヴェイユ表現とSL(2,R)の普遍被覆群の既約ユニタリ表現とのテンソル積によって得られる。従って、 は、ヤコビ群のヴェイユ表現とSL(2,R)の普遍被覆群の既約ユニタリ表現とのテンソル積によって得られる。従って、 は無限次元であり、この差分微分方程式系を解くことは易しくない。 は無限次元であり、この差分微分方程式系を解くことは易しくない。 また、このような無限次元表現 に対する、一般化されたホイッタカー模型の重複度は今までほとんど研究されていないことにも注意したい。 に対する、一般化されたホイッタカー模型の重複度は今までほとんど研究されていないことにも注意したい。 |