| 内容要旨 | | 1.INTRODUCTION 複素多様体としてのCalabi-Yau多様体の理論は最近ミラーシンメトリーとも関連して目覚しい発展を遂げています.そこでそれを手本として,70年及び80年代から精力的に研究が進められて来た正標数K3曲面の理論を使い,正標数Calabi-Yau多様体の理論が構成出来ないだろうかという動きが最近起こり始めています.ここではそれに関連した幾つかの話題のうち特に超特異Calabi-Yau threefoldについて調べます. 定義1.1.Xを正標数代数閉体上定義された三次元非特異射影代数多様体とする.もしKX OXかつh1(OX)=h2(OX)=0が満たされる時XをCalabi-Yau threefoldと呼ぶ. OXかつh1(OX)=h2(OX)=0が満たされる時XをCalabi-Yau threefoldと呼ぶ. 正標数C.Y.の重要な特徴の一つに,次で与えられる高さと呼ばれる不変量が定まることが挙げられます. 定義1.2(Artin-Mazur[1.]).XをC.Y.threefoldとしたとき,Xに付随した高さht(X)を以下で定める.  また,WOXをSerreが定義したWittベクトル環の層としたとき,上の定義は以下と同値であることが知られている  但し,KはWittベクトル環W(k)の商体とする.特にht(X)=∞のときXを超特異C.Y.と呼ぶ. M.ArtinはK3曲面に付随した形式群(形式Brauer群)を上と同様に定義し,その高さを用いて変形のstratificationを与えたのだが,この不変量はまた正標数の病理的現象と深く関っていることが知られている.ところで正標数での多様体を考えた時,最も困難な点の一つに標数零の時のような完全な形のHodge理論が存在しないことが挙げられるが,それに関連して以下の問題が考えられる: 問題1.3. i)XをC.Y.threefoldとしたとき,以下の等式は成立するか?  ii)C.Y.threefold Xにはどの様な正標数特有のファイブレーションが存在するか? (i)の等式が成立することはXについてHodge duality  が成立することと同値であることが容易に確かめられる.勿論,この先の段階としてはHodge spectral sequenceの退化, が成立することと同値であることが容易に確かめられる.勿論,この先の段階としてはHodge spectral sequenceの退化, のトーション部分の有無などが問題として考えられる. のトーション部分の有無などが問題として考えられる. 特にXがK3曲面の場合には上の問題は次のように解決されている:等式  は最初にRudakov-Shafarevich[13]が超特異K3曲面の楕円ファイブレーションの構造を調べることで示し,更にNygaard[11]はde Rham-Witt complexから定まるコホモロジー(Hodge-Wittコホモロジー)を用いることで別証を与えた.特にK3曲面の場合,上記の結果よりHodge spectral sequence  がE1-項で退化し,またde Rham betti数 はl-adic betti数 はl-adic betti数 と一致することが従う. と一致することが従う. また(ii)に関連して,K3曲面Xが準楕円ファイブレーションを持つための必要十分条件はXが超特異(塩田氏の定義で),かつp=2又はp=3でArtin不変量 0 0 6であることが知られている(cf.[14]). 6であることが知られている(cf.[14]). そこで問題の正標数C.Y.threefoldについてであるが,現在以下のことが分かっている. 定理1.4(宮岡[10]).XをC.Y.threefoldとする.もしH0(TX)が零でないなら以下の二つの場合を除いてXはuniruledである,i) ,又はii)H0(TX)=kでこのグローバルセクションによるインクルージョンのコカーネルTX/OXが局所フリー. ,又はii)H0(TX)=kでこのグローバルセクションによるインクルージョンのコカーネルTX/OXが局所フリー. 定理1.5.XをC.Y.threefoldとした時,もしXがuniruledならばXは超特異である. また諏訪紀幸氏はHodge-WittコホモロジーについでEkedahl dualityを適用することで以下の定理が成り立つことを指摘した(cf.[17]). 定理1.6.XをC.Y.threefoldとしたとき,もしPicXがpトーションフリーであれば が成立する. が成立する. 上の諸定理は問題1.3および超特異C.Y.の関係について示唆的である.そこで以下ではどの様な正標数の病理的現象が実際に起こるかを例を構成して調べる. 2.主結果 ここでは超特異C.Y.threefoldを実際に構成し,正標数での病理的現象について調べる.扱う構成法は以下の二つである (I)有理準楕円曲面と有理楕円曲面のファイバー積として, (II) 上のp-閉有理ベクトル場の商として. 上のp-閉有理ベクトル場の商として. 構成(I).C.Schoenは有理楕円曲面二つのファイバー積を 上に取ることでC.Y.threefoldが構成されることを示した.ここでは彼の方法を真似て,一方を有理準楕円曲面とした時どの様になるかを考察する. 上に取ることでC.Y.threefoldが構成されることを示した.ここでは彼の方法を真似て,一方を有理準楕円曲面とした時どの様になるかを考察する.  ここで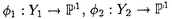 はそれぞれ有理楕円曲面及び有理準楕円曲面でセクションを持つとする.更に,全てのファイバーのコンポーネントは被約と仮定した時,以下が成り立つ(cf.[16]): はそれぞれ有理楕円曲面及び有理準楕円曲面でセクションを持つとする.更に,全てのファイバーのコンポーネントは被約と仮定した時,以下が成り立つ(cf.[16]): i)Wは高々孤立超曲面特異点をもつ, ii)Wのdualizing sheafはtrivial. そこで特異点解消 : : →Wを考える訳であるが,以下の定理が成立することがわかる. →Wを考える訳であるが,以下の定理が成立することがわかる. 定理2.1. 1, 1, 2を以下のような可約ファイバーのみを持つとする: 2を以下のような可約ファイバーのみを持つとする:  更に が満たされる様 が満たされる様 .上にファイバー積を取った場合small resolution .上にファイバー積を取った場合small resolution  : : →Wが存在する.実際にこれ等を満たす →Wが存在する.実際にこれ等を満たす 1, 1, 2は存在し以下が成立する: 2は存在し以下が成立する: i) はCalabi-Yau threefoldである,i.e., はCalabi-Yau threefoldである,i.e.,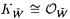 ,h1( ,h1( )=h2( )=h2( )=0, )=0, ii) はunirational,即ち超特異C.Y., はunirational,即ち超特異C.Y., iii) iv)b2( )=27if p=2,b2( )=27if p=2,b2( )=35if p=3が成立する, )=35if p=3が成立する, v) である,即ちHodge dualityが成立する. である,即ちHodge dualityが成立する. vi) 上ファイブレーションで一般ファイバーが,(a)楕円曲線とカスプを一つ持つ有理曲線との直積,及び(b)有理二重点を持つK3曲面であるようなものが存在する. 上ファイブレーションで一般ファイバーが,(a)楕円曲線とカスプを一つ持つ有理曲線との直積,及び(b)有理二重点を持つK3曲面であるようなものが存在する. 更に上定理vi)で云うファイバー構造についてY2:有理曲面より, -ファイブレーション構造 -ファイブレーション構造 ( ( 上のファイブレーションで一般ファイバーが 上のファイブレーションで一般ファイバーが と同型なもの)が存在し,射の合成により と同型なもの)が存在し,射の合成により のファイブレーション のファイブレーション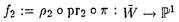 を誘導する.特に,f2の一般ファイバーは次のファイバー積で与えられる: を誘導する.特に,f2の一般ファイバーは次のファイバー積で与えられる:  よって二重被覆 による による の底変換を観察することでf2の一般ファイバーが決定できる. の底変換を観察することでf2の一般ファイバーが決定できる. 定理2.2.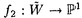 の一般ファイバーは の一般ファイバーは (1)p=3の時K3曲面. (2)p=2の時K3曲面及び12個の有理二重点A1を持つ正規曲面で超特異K3曲面と双有理. またY2の代わりにY1の -ファイブレーション -ファイブレーション を同様に考えることで,以下のような を同様に考えることで,以下のような のファイブレーション のファイブレーション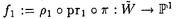 が存在することが判る. が存在することが判る. 定理2.3. の一般ファイバーは の一般ファイバーは (1)p=3の時2個の有理二重点A2を持つ正規曲面で超特異K3曲面と双有理, (2)p=2の時1個の有理二重点D4を持つ正規曲面で超特異K3曲面と双有理. また はその構成法より一般ファイバーが楕円曲線とカスプを一つ持つ有理曲線との直積であるような はその構成法より一般ファイバーが楕円曲線とカスプを一つ持つ有理曲線との直積であるような 上ファイブレーションを持つことが判る.この様な特異な一般ファイバーを持つファイブレーションは超特異K3曲面の準楕円ファイブレーションとも関連して興味深い対象である. 上ファイブレーションを持つことが判る.この様な特異な一般ファイバーを持つファイブレーションは超特異K3曲面の準楕円ファイブレーションとも関連して興味深い対象である. 構成(II).ここでは正標数特有のp-閉ベクトル場による商多様体の構成を用いる(cf.[13]).即ちZを非特異多様体とし,その上の有理ベクトル場 でp-閉なもの(i.e., でp-閉なもの(i.e.,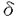 P= P= 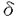 for some for some  ∈k(Z))を一つ取る.この時,正規多様体Vが商として得られ,Zの相対フロベニウス射はVを経由する. ∈k(Z))を一つ取る.この時,正規多様体Vが商として得られ,Zの相対フロベニウス射はVを経由する.  gは有限,純不分離射で次数pである.この様にして得られるVは勿論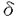 の取り方によって様々に変化するのであるが,ここではZとして三次元有理多様体を考え,その商としてC.Y.threefoldを構成する. の取り方によって様々に変化するのであるが,ここではZとして三次元有理多様体を考え,その商としてC.Y.threefoldを構成する. 定理2.4.以下のような 上のp-閉有理ベクトル場を考える: 上のp-閉有理ベクトル場を考える: 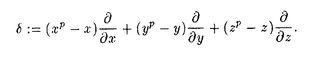 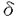 による商を による商を とする.ここで標数p=3の時,Vはcrepant resolution とする.ここで標数p=3の時,Vはcrepant resolution :X→Vを持ち,以下が成り立つ: :X→Vを持ち,以下が成り立つ: i)XはCalabi-Yau threefoldである, ii)Xはunirational,即ち超特異C.Y., iii) iv)b2(X)=41,b3(X)=0が成立する, v)h0( X)=h0(TX)=0である,即ちHodge dualityが成立する, X)=h0(TX)=0である,即ちHodge dualityが成立する, vi)Xは準楕円ファイブレーションを持つ. 注意2.5.上の(I),(II)のようにして得られたC.Y.threefoldは次の形のHodge diamondを持つ,  特に(II)で構成された例Xについて,b3=0であるためXは標数零に持ち上がらないことがわかる.このことは全てのK3曲面は標数零に射影的に持ち上がる(P.Deligne[2])という性質がC.Y.threefoldでは必ずしも成立しないことを示している. REFERENCES1.M.Artin,B.Mazur,Formal groups arising from algebraic varieties,Ann.Sci.Ecole Norm.Sup.(4eserie)10,87-132(1977).2.P.Deligne,Relevement des surfaces K3 en caracteristique nulle,Lect.Notes in Math.868,Springer-Verlag,58-79,(1981).3.M.Hirokado,Zariski surfaces as quotients of Hirzebruch surfaces by 1-foliations,preprint.4.___,Calabi-Yau threefolds obtained as fiber products of elliptic and quasi-elliptic rational surfaces,preprint.5.___,Calabi-Yau threefolds in characteristic p,preprint.6.H.Ito, The Mordell-Weil groups of unirational quasi-elliptic surfaces in characteristic 3,Math.Z.,211,1-40(1992).7.___,The Mordell-Weil groups of unirational quasi-elliptic surfaces in characteristic 2,Tohoku Math.J.,46,211-251(1994).8.W.Lang,Extremal rational elliptic surfaces in characteristic p,Math.Z.207,429-438(1991).9.W.Lang,N.Nygaard,A short proof of the Rydakov-Safarevic theorem,Math.Ann.251,171-173(1980).10.Y.Miyaoka,Vector fields on Calabi-Yau manifolds in characteristic p,代数幾何学シンポジュウム記録(於城崎),149-156(1995).11.N.Nygaard,On the fundamental group of a unirational 3-fold,Inv.Math.44,(1978),75-86.12.___,A p-adic proof of the non-existence of vectorfields on K3 surfaces,Ann. of Math.110,515-528(1979).13.A.Rudakov,I.Shafarevich,Inseparable morphisms of algebraic surfaces,Math.USSR Izv,10,1205-1237(1976).14.___,Surfaces of type K3 over fields of finite characteristics,J.Soviet Math.22,1476-1533(1983).15.K.Sakamaki,Artin-Mazur formal groups and Picard-Fuchs equations attached to certain Calabi-Yau threefolds, Master’s Thesis,Kyoto University,1994.16.C.Schoen,On fiber products of rational elliptic surfaces with section,Math.Z.197,177-199(1988).17.N.Suwa,Hodge-Witt cohomology of complete intersections,J.Math.Soc.Japan,vol.45,no.2,295-300(1993). |
| 審査要旨 | | kを代数的閉体,Xをk上の非特異完備代数多様体とする.n次元射影多様体PnからXへの支配的な有理写像が存在する時,Xを単有理多様体という.また,標準束 Xが自明的でHi(X,OX)=0(i=1,…,n-1)がなりたつとき,XをCalabi-Yau多様体という.n=1の場合には,単有理曲線が有理曲線と同義語となることは,Lurothの定理として知られている.また,Calabi-Yau曲線は楕円曲線であり,よく研究された古典的な対象である.n=2の場合にも,kの標数が0ならば単有理曲面は有理曲面と同義語になる.また,標数が何であってもCalabi-Yau曲面はK3曲面とよばれるものに他ならない.2次元の場合,正標数における非有理的な単有理曲面の存在は1958年にZariskiによって示された.その後,1970年代になって,Artin,Shioda,Katsura,Rudakov,Shafarevich等によって非有理的な単有理曲面の構造がかなり明確にされた.n=3の場合には,kの標数が0であっても非有理的な単有理曲面が存在する.また,3次元のCalabi-Yau多様体は素粒子論にも登場するようになり,少なくとも標数0においては,Morrison,Wilson,Roan,Katz,Witten,Aspinwall,Batyrevをはじめ数多くの研究者によって現在,構造の解明が行われている.このような状況において,廣角正行は正標数において,単有理曲面および3次元のCalabi-Yau多様体をとりあげ,それらを有理ベクトル場を組織的に用いて研究し,以下のような3篇の論文を作成した. Xが自明的でHi(X,OX)=0(i=1,…,n-1)がなりたつとき,XをCalabi-Yau多様体という.n=1の場合には,単有理曲線が有理曲線と同義語となることは,Lurothの定理として知られている.また,Calabi-Yau曲線は楕円曲線であり,よく研究された古典的な対象である.n=2の場合にも,kの標数が0ならば単有理曲面は有理曲面と同義語になる.また,標数が何であってもCalabi-Yau曲面はK3曲面とよばれるものに他ならない.2次元の場合,正標数における非有理的な単有理曲面の存在は1958年にZariskiによって示された.その後,1970年代になって,Artin,Shioda,Katsura,Rudakov,Shafarevich等によって非有理的な単有理曲面の構造がかなり明確にされた.n=3の場合には,kの標数が0であっても非有理的な単有理曲面が存在する.また,3次元のCalabi-Yau多様体は素粒子論にも登場するようになり,少なくとも標数0においては,Morrison,Wilson,Roan,Katz,Witten,Aspinwall,Batyrevをはじめ数多くの研究者によって現在,構造の解明が行われている.このような状況において,廣角正行は正標数において,単有理曲面および3次元のCalabi-Yau多様体をとりあげ,それらを有理ベクトル場を組織的に用いて研究し,以下のような3篇の論文を作成した. 第1論文においては,3次元射影多様体P3のある有理ベクトル場による商多様体を研究している.構成の仕方から,この商多様体は単有理的になるが,さらにこの多様体の数値的な不変量を計算している.とくに,標数が3のときには,商空間の非特異モデルとしてCalabi-Yau多様体が得られるが,本論文において,このCalabi-Yau多様体が標数0には持ち上がらないことを第3Betti数を用いて示している.2次元のときには,2次元Calabi-Yau多様体であるK3曲面は必ず標数0に持ち上がることがDeligneによって示されており,この例の発見は2次元と3次元では状況がまったく違うことを示す注目に値いするものである. 第2論文においては,P1上の有理的な楕円曲面とP1上の有理的な準楕円曲面のファイバー積からCalabi-Yau多様体を構成することを考えている.この方法はSchoenによる標数0の場合の類似であるが,特異点の扱いが難しくなる.本論文において,この方法によって,一般のファイバーに特異点があるという正標数特有のファイバー空間の構造を持つCalabi-Yau多様体を構成し,それが単有理多様体であることを示している.また,そのArtin-Mazur形式群の高さが∞であることを示している. 第3論文においては,Hirzebruch曲面の有理ベクトル場による商曲面を研究している.商曲面として一般型曲面,K3曲面などが得られるが,構成の仕方から,これらはいずれも単有理曲面になる.本論文において,構成した曲面の数値的な不変量を計算している.これらは正標数に特有の現象を示す例として貴重なものである. 本論文は,このように,正標数特有の現象をとりあげ,有理ベクトル場を巧妙にあやつりながら新しい現象を発見し,また多くの例を提供する大変興味深いものであり,この方面の研究に-石を投じ,貢献するものである.よって、論文提出者廣門正行は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |