要旨 k次対称群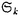 の通常表現の指標はべき和の積をkの分割で特徴付けされるSchurのS関数と呼ばれる対称関数の基底で展開したときの係数として現れ,指標表はこの変換公式によって完全に決定する.I.Schurはこれと似た方法で,対称群の射影表現の指標を完全に決定した([S],Thorem0.6を参照).このとき,射影表現の指標値は奇数次のべき和の積を,Q関数と呼ばれる対称関数の基底で展開することで得られる.通常表現の場合に用いられた方法の背後には,対称群と一般線形群GL(n)のdualityの関係(ある表現の上でお互いのcentralizerとして作用する関係)がある.実は,SchurのS関数は一般線形群の既約な多項式表現の指標を与える.このことから,対称群の射影表現の場合にも何らかのdualityの関係が存在することが期待される.そして,さらにはその相手として現れる結合代数の既約表現の指標がQ関数になっていることも推測される.このアプローチに近いものとして,A.N.Sergeevが,あるB型Weyl群のねじれ群環BkとLie superalgebra Q(n)の
の通常表現の指標はべき和の積をkの分割で特徴付けされるSchurのS関数と呼ばれる対称関数の基底で展開したときの係数として現れ,指標表はこの変換公式によって完全に決定する.I.Schurはこれと似た方法で,対称群の射影表現の指標を完全に決定した([S],Thorem0.6を参照).このとき,射影表現の指標値は奇数次のべき和の積を,Q関数と呼ばれる対称関数の基底で展開することで得られる.通常表現の場合に用いられた方法の背後には,対称群と一般線形群GL(n)のdualityの関係(ある表現の上でお互いのcentralizerとして作用する関係)がある.実は,SchurのS関数は一般線形群の既約な多項式表現の指標を与える.このことから,対称群の射影表現の場合にも何らかのdualityの関係が存在することが期待される.そして,さらにはその相手として現れる結合代数の既約表現の指標がQ関数になっていることも推測される.このアプローチに近いものとして,A.N.Sergeevが,あるB型Weyl群のねじれ群環BkとLie superalgebra Q(n)の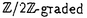 代数としてのdualityの関係をQ(n)の自然表現
代数としてのdualityの関係をQ(n)の自然表現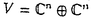 (n+n次元)のk-階のテンソル積
(n+n次元)のk-階のテンソル積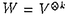 の上に構成し,Q(n)の既約表現の指標がQ関数で表されることを示している([Se,Theorem3,Theorem4],Theorem2.2参照).この論文では,対称群のねじれ群環AkとLie superalgebara Q(n)のdualityを示した.それによって,Schurの結果がこの表現を用いて読み直される.このdualityはSergeevが得たBkとQ(n)のdualityを制限して得られる.この方法を用いるために,Bkの既約表現とAkの既約表現の関係を調べた.興味深い事実として,Akはさほど自明ではない代数射によってBkの中に埋め込まれる.さらに,この埋め込みによってBkがAkとk次のClifford代数Ckとの(
の上に構成し,Q(n)の既約表現の指標がQ関数で表されることを示している([Se,Theorem3,Theorem4],Theorem2.2参照).この論文では,対称群のねじれ群環AkとLie superalgebara Q(n)のdualityを示した.それによって,Schurの結果がこの表現を用いて読み直される.このdualityはSergeevが得たBkとQ(n)のdualityを制限して得られる.この方法を用いるために,Bkの既約表現とAkの既約表現の関係を調べた.興味深い事実として,Akはさほど自明ではない代数射によってBkの中に埋め込まれる.さらに,この埋め込みによってBkがAkとk次のClifford代数Ckとの(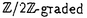 代数としての)テンソル積と同型であることがしたがう.そして,Bkの既約表現はAkの既約表現とCkの既約表現のテンソル積として構成される.これにより,Bkの既約表現のAkへの制限が簡潔に記述できる(具体的には,Bkの既約表現はAkの表現として(
代数としての)テンソル積と同型であることがしたがう.そして,Bkの既約表現はAkの既約表現とCkの既約表現のテンソル積として構成される.これにより,Bkの既約表現のAkへの制限が簡潔に記述できる(具体的には,Bkの既約表現はAkの表現として(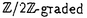 の意味で)等質空間であり,その中の既約表現の重複度は2のべきである).これらの最終的な結果として,AkとQ(n)のdualityを与えるQ(n)自然表現のk-階テンソル積Wの部分空間を得た.
の意味で)等質空間であり,その中の既約表現の重複度は2のべきである).これらの最終的な結果として,AkとQ(n)のdualityを与えるQ(n)自然表現のk-階テンソル積Wの部分空間を得た.
ただし,ここで述べられたBkやAkやQ(n)の既約表現を与えるWの部分空間(の基底)を具体的に与えるという問題はまだ未解決である.そこで,この問題を(BkやAkについて)解く助けになると期待されるものとして,BkやAkのcharacteristic mapがある(Theorem5.1を参照).この写像は,表現の同型類で張られる結合代数から対称関数環への代数射であるが,BkやAkの既約表現の同型類は,charascteristic mapによって,Q関数(の定数倍)に移されるという事実がある.すなわち,このcharacteristic mapは同型射であり,その像によって表現の等質空間分解が一意に定まる.この性質を利用してある表現について(必ずしも既約ではない)具体的に表現空間を与えた.