| 内容要旨 | | 有限要素法は偏微分方程式等の有力な実用的数値解法の一つであり,その手法の基本部分はほぼ確立されているが,他方で現在も改良や数学的解析が続けられている。本論文では,平面上の四辺形形状のいくつかの有限要素(略して要素とも呼ぶ)について,有限要素法の数学的解析の基礎となる,いわゆる補間誤差解析を実施したものである。特に最近提出された修正8節点四辺形セレンディピティ要素及び関連する諸四辺形要素について詳しく論じており,数値実験的に理論の検証も行っている。数学的結果の主要なものは3つの定理にまとめてあるが,関連する諸結果の提出と注意も与えている。 第一章は序章で,有限要素法の役割やその誤差解析について概論を与え,さらに本論文の内容を概観したものである。 第二章は準備の章で,以下で使用する記号やSobolev空間の導入をし,加えて多項式による近似の誤差などにつき,既知の結果をまとめたものである。 第三章は有限要素の紹介の章で,まず有限要素の基本的な概念と性質を説明した上で,代表的な2次元の三角形及び四辺形要素を例示した。特に四辺形要素については以下の章で扱うので,アイソパラメトリック変換とあわせてやや詳しく説明した。さらに本論文で主に解析する修正8節点セレンディピティ要素につき,必要な性質の要点を解説した。 第四章は主要結果を述べた章である。まず,有限要素法の誤差解析の原理と,そこで補間誤差評価の果たす役割を説明した上で,修正8節点セレンディピティ要素のうち菊地-岡部-藤尾の提案によるものにつき,3つの定理とその証明の形で各要素での補間誤差評価式を導びき示した。ただし,補間誤差とは,対象となる関数とその有限要素補間関数の間の誤差を意味する。さらに関連諸要素についても注意を与え,主要な結果の要点を示し,必要な場合には証明のポイントとなる部分を説明した。 最初に,四辺形が通常の直辺凸四辺形の場合につき,正則四辺形族の概念を与え,その上でアイソパラメトリック変換が双1次の場合につき,評価式を導いた。結果は次の定理1にまとめられている(記号の説明は一部省略)。 定理1 直辺四辺形要素族{K}は,次の正則条件を満たすと仮定する。  ただし,hKは要素Kの直径,h’KはKの最短辺長, KはKの内角の余弦の絶対値中の最大値であり, KはKの内角の余弦の絶対値中の最大値であり, と と は族のみに依存する正定数である。このとき,u∈W3,p(K)→C(K) は族のみに依存する正定数である。このとき,u∈W3,p(K)→C(K) に対する補間関数 に対する補間関数 Kuは,次の不等式を満たす。 Kuは,次の不等式を満たす。 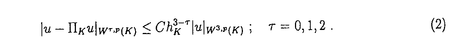 ただし,例えば はソボレフ空間 はソボレフ空間 のセミノルムであり,またC=C( のセミノルムであり,またC=C( ,p, ,p, , , )は )は ,p, ,p, , , に依存するがhKとuには依存しない正定数である。□ に依存するがhKとuには依存しない正定数である。□ この定理は標準的な手法で証明できるが,後の定理の場合の証明との差異を明確にするために,証明の要点を記述してある。 上記で正則な四辺形族とは,大まかには,各四辺形の辺長が同程度で,各内角も0と から一定以上離れた値をとることを意味する。実際には,この条件を満たさず,内角が平角に近かったり,ある辺長が他の辺長に比較して非常に小さい場合も考慮したい場合がある。その極端な場合は,四辺形が三角形に縮退した場合である。この論文では,次にこのような場合を考察した。ただし,四辺形(あるいは三角形)が極端に平たくなる場合は除外した。結果は次の定理2のようにまとめられる。 から一定以上離れた値をとることを意味する。実際には,この条件を満たさず,内角が平角に近かったり,ある辺長が他の辺長に比較して非常に小さい場合も考慮したい場合がある。その極端な場合は,四辺形が三角形に縮退した場合である。この論文では,次にこのような場合を考察した。ただし,四辺形(あるいは三角形)が極端に平たくなる場合は除外した。結果は次の定理2のようにまとめられる。 定理2 直辺四辺形要素族{K}は,次の条件を満たすと仮定する。  ただし, KはKの中に含まれる円板の直径の上限,hKは定理1と同様, KはKの中に含まれる円板の直径の上限,hKは定理1と同様, *は族のみに依存する正定数である。このとき,u∈W3,pK(K)→C(K)に対する補間関数 *は族のみに依存する正定数である。このとき,u∈W3,pK(K)→C(K)に対する補間関数 Kuは,次の不等式を満たす。 Kuは,次の不等式を満たす。   ただし,C=C(p, *)はpと *)はpと *には依存するがhKとuには依存しない正定数である。□ *には依存するがhKとuには依存しない正定数である。□ この証明には,Jametによる四節点双1次四辺形要素に関する考察と手法,結果を本質的に利用した。ただし,トレース定理の部分については彼の論法に不十分と思われる点があったので,ZenisekとVanmaeleの手法を応用し改めて証明した。また(5)でpに制限があるのは,変換のヤコビアンの評価に起因する。 以上はいずれも,四辺形の辺が直線状の場合であるが,一般のアイソパラメトリック変換の場合には,本要素では辺は曲線弧(実は放物線の一部)になる。このようなより一般の場合も有限要素法ではしばしば用いられるので,次にこの場合を考察した。ただし,曲辺四辺形族としては,基礎となる直辺四辺形族が先の意味で正則で,曲辺上の中間節点が基礎となる直辺四辺形の辺の中点から少ししかずれていない(距離が は基礎となる直辺四辺形の直径)場合に限った。この場合を,曲辺四辺形要素族として正則と称する。結果は次の定理3のとおりである。 は基礎となる直辺四辺形の直径)場合に限った。この場合を,曲辺四辺形要素族として正則と称する。結果は次の定理3のとおりである。 定理3 アイソパラメトリック変換の下で,正則条件を満たす曲辺修正8節点セレンディピティ要素族を考える。十分小さいhKに対しては(即ち,∀hK h0;ただし,h0=h0( h0;ただし,h0=h0( , , , , )は )は , , , , のみに依存する正定数), のみに依存する正定数), に対する補間関数 に対する補間関数 Kuは,次の不等式を満たす。 Kuは,次の不等式を満たす。  ただし,C=C( ,p, ,p, , , )は )は ,p, ,p, , , に依存するが,hK( に依存するが,hK( h0)とuには依存しない正定数である。□ h0)とuには依存しない正定数である。□ この定理の証明は,基礎となる直辺四辺形要素に関して定理1を用いた上で,曲辺四辺形との間の座標変換による摂動を詳しく評価することにより与えられる。その指針として,Ciarletによるアイソパラメトリック要素の誤差解析手法が役立った。なお,(6)で低次の項 が入ったのは,一般のアイソパラメトリック変換の評価に伴なうものである。 が入ったのは,一般のアイソパラメトリック変換の評価に伴なうものである。 第四章の残りの部分では,他のタイプの修正8節点セレンディピティ要素や,4節点四辺形要素,9節点四辺形要素,さらに本来の8節点セレンディピティ要素についての結果の概要を示してある。証明の方針は前の場合とほぼ同様なので証明自体は省略したが,9節点要素については証明で先と異なる部分のポイントを示してある。なお,修正8節点セレンディピティ要素の中には,MacNealとHarderが提出した著名なものも含まれ,先に論じた要素(菊地-岡部-藤尾)と同程度の誤差評価式が得られる。 第五章は,第四章で考察した様々な四辺形要素につき,要素形状と関数を具体的に何通りか与え,その各要素での補間誤差を実際に数値的に計算し,理論で示された結果(特に要素直径hKに関するオーダー)と比較した結果をまとめたものである。要素形状としては直辺四辺形と曲辺四辺形の双方を扱い,前者については三角形に縮退もしくはほとんど縮退する場合も含めた。全体として,理論との一致は良好と思われ,特に8節点セレンディピティ要素についての修正により実際に誤差のhKに関するオーダーが改善されていることが確認できた。なお,元来のセレンディピティ要素では誤差のhKに関するオーダーは一般に1次低くなる。 第六章は結論の章であり,修正8節点セレンディピティ要素が本来のセレンディピティ要素より精度が改善されたことが理論的に示されたこと等を述べ,さらに未解決の課題として,曲辺で縮退する場合の解析を挙げている。 さらに文献表,図,表などを示して本論文は終わっている。 |