本論文では3次の非線形媒質における2波相互作用方程式系の定在波について考察する。まず3次の非線形光媒介における2波相互作用に現れる次の連立のSchrodinger方程式系を考える。

　ここで＝(t,x)と＝(t,x)は二つの相互作用波の複素振幅をそれぞれに表し;r,qとa_jk(j,k＝1,2)は実定数,かつr<0,q<0である。次は相互作用場に現われる次の連立のKlein-Gordon方程式系を考える。

　ここで＝(t,x)と＝(t,x)は二つの実数値関数であり,m_j,a_jk(j,k＝1,2)は実定数,かつm₁>0,m₂>0は二つの質量である。

　我々は次の三つの問題に興味をもっている。1⁰.二次元と三次元の空間における基底状態の定在波の存在。2⁰.基底状態の定在波の安定性と不安定性。3⁰.時間発展問題の大域解の存在性とblowupのsharpな条件。

　とりあえず,a_jk(j,k＝1,2)は次の仮定とする。

　じつは,以上の仮定は(1)と(2)の定在波が存在するためのほとんど必要条件である。では,まず(1)を考察する。さきに次のようにおく。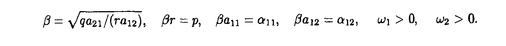

　これから次の三次の非線形項を持つ連立楕円方程式系を考える。

　そして,もし(u,v)＝(u(x),v(x))は(4)を満たすなら,は(1)の定在波と呼ぶ。

　空間二次元のときに,u,v∈H¹(R²)に対して,次の二つの汎関数を定義する: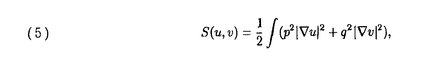

　空間三次元のときに,u,v∈H¹(R³)に対して,次の二つの汎関数を定義する:

　(5)と(7)の中のSは(u,v)の作用(action)と呼ぶ。それに,空間二次元と三次元の両方に対して,次の集合を定義する。

　これから,次の条件付き極値問題を考える。

　そしてscaling argument,Straussのcompactness lemma,関数の対称再配分などの変分法的手法を用いて,(1)の定在波の存在の定理を示す。

　定理1 N＝2,3とする。このとき,ある(,)∈Mが存在して,次の性質を持っている。

　1⁰.(,)は変分問題(10)の解になる。即ち

　2⁰.(,)は(4)の最小作用を持つ解になる。

　3⁰.(x),(x)は|x|の対称関数であり,無限遠で指数的に減衰する。

　定理1の2⁰によって,(,)は(4)の基底状態という。自然には(1)の基底状態の定在波という。次は(1)のCauchy問題のblowupの性質にから,(1)の基底状態の定在波の不安定性が得られる。

　定理2 N＝2,3とする。このとき,任意の>0に対して,ある(₀,₀)∈H¹(R^N)×H¹(R^N)が存在してかつ次の性質を満たす。初期値(₀,₀)を持つ(1)の解(,)は有限時間でblowupする。

　更に,(4)の基底状態の性質と(1)の時間発展問題から生成される流れの不変集合から,(1)のCauchy問題の大域解の存在性についてのsharpな条件を得られる。

　定理3空間二次元と三次元の両方に対し,H(u,v)は(7)と同様のS(u,v)とおく。もし(₀,₀)は

　を満たすなら,初期値(₀,₀)を持つ(1)の解(,)は大域的にt∈[0,∞)で存在する。

　注意するのは空間二次元のhと空間三次元のhが違う。基底状態(,)は空間二次元と三次元の両方に対して,H(,)＝hを満たす。そして定理2によって,定理3に得られる大域解の存在性についての条件はsharpな条件と言う。

　次に,(2)を考察する。またN＝2,3とおく。次の三次の非線形項を持つ連立楕円方程式系を考える。

　もし(u,v)＝(u(x),v(x))は(11)を満たすなら,((t,x),(t,x))＝(u(x),v(x))は(2)の定常波になる。これから,(u,v)∈H¹(R^N)×H¹(R^N)(N＝2,3)に対して,とおいて,次の二つの汎関数を定義する。

　(12)のSは(u,v)の作用(action)という。それに,次の集合を定義する。

　それから,またscaling argument,Straussのcompactness lemma,関数の対称再配分などの変分法的手法を用いて,(2)の定常波の存在定理を示す。

　定理4 ある(,)∈M存在して,次の性質を満たす。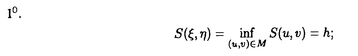

　2⁰.(,)は(11)の最小作用を持つ解になる。

　定理 4の1⁰によって,(,)は(11)の基底状態という。自然に((t,x),(t,x))＝((x),(x))は(2)の基底状態の定常波という。次は(2)のCauchy問題のblowupな性質から,(2)の基底状態の定常波の不安定性が得られる。

　定理5 N＝2,3とする。このとき,任意の>0に対して,ある(₀,₀)∈H¹(R^N)×H¹(R^N)が存在して,かつ次の性質を満たす。

　初期値

　を持つ(2)の解(,)は有限時間でblowupする。

　(2)に対して,次の初期値を考える。

　初期値(16)に対して,次のエネルギEを定義する。

　ここでSは(12)と同じ。(11)の基底状態の性質と(2)の発展問題から生成された流れの不変集合から,(2)のCauchy問題の大域解の存在性についてのSharpな条件を得られる。

　定理 6(₀,₀)と(₁,₁)はE<hを満たすとする。

　1⁰.もし(₀,₀)がQ(₀,₀)<0を満たすなら,初期値(16)を持つ(2)の解(,)は有限時間でblowupする。

　2⁰.もし(₀,₀)がQ(₀,₀)>0を満たすなら,初期値(16)を持つ(2)の解(,)は大域的にt∈[0,∞)で存在する。

　論文提出者は、3次の非線形媒質において2波が相互作用する場合の現象を記述する方程式系に対して、定在波解及び定常解と呼ばれる広い意味でのソリトン解の不安定性について解析した。具体的には、次ような非線形シュレディンガー方程式の連立系

　$113743f27.gif$

　$113743f28.gif$

　と次のような非線形クライン-ゴルドン方程式の連立系

　$113743f29.gif$

　$113743f30.gif$

　を考える。但し、∂_t＝∂/∂tとし、r,q<0かつm₁,m₂>0であり、実定数a_jk(j,k＝1,2)は次を満たすものとする。

　$113743f31.gif$

　ここで、方程式系(1)-(2)に対しては、次の非線形楕円型方程式系の非自明解(,)を考える。

　$113743f32.gif$

　$113743f33.gif$

　このとき、

　$113743f34.gif$

　とおくと、関数(U,V)は非線形シュレディンガー方程式系(1)-(2)の解となり、このような解を(1)-(2)の定在波解(standing wave solution)と呼ぶ。さらに、方程式系(3)-(4)に対しては、次の非線形楕円型方程式系の非自明解(,)を考える。

　$113743f35.gif$

　$113743f36.gif$

　このとき、

　$113743f37.gif$

　とおくと、関数(U,V)は非線形クライン-ゴルドン方程式系(3)-(4)の解となり、このような解を(3)-(4)の定常解(stationary solution)と呼ぶ。

　考える空間次元は2次元または3次元(すなわち、n＝2,3)とする。まず論文提出者は、変分法的手法を用いて非線形楕円型方程式系(6)-(7)と(9)-(10)の非自明解のうち作用(action)が最小である解、すなわち最小作用解(,)を求めた。さらに、それらを用いて(8)及び(11)から作られる定在波解または定常解(U,V)の不安定性を、(U,V)のどんな小さな近傍に対してもその近傍のある点から出発する方程式系(1)-(2)及び(3)-(4)の解で有限時間内にエネルギー空間(すなわちH¹(Rⁿ))の位相で爆発するものがあることを示すことにより証明した。また、その結果の証明の系として、方程式系(1)-(2)及び(3)-(4)の解が時間大域的に存在するための初期値の十分条件を与えた。

　従来単独の非線形シュレディンガー方程式や非線形クラインーゴルドン方程式に対しては類似の結果が知られていたが、連立方程式系に対しては余り研究がなされていなかった。方程式系(1)-(2)及び(3)-(4)は数理科学的に重要な方程式系であることを考え合わせると、論文提出者によって得られた結果の数理科学的な意義は大きいものと言って良い。以上により、論文提出者 張健 氏は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。