| 内容要旨 | | 本論文の目的は大別して以下の二点からなる.第一に,曲面の周期的自己同型の可約性と -不変量の関係を明らかにする.第二に,曲面の超楕円的写像類群上Meyer関数を定義し,それに対するいくつかの明示公式を与える.これら二つの対象は,符号数双対輪体を通して互いに密接に関係している. -不変量の関係を明らかにする.第二に,曲面の超楕円的写像類群上Meyer関数を定義し,それに対するいくつかの明示公式を与える.これら二つの対象は,符号数双対輪体を通して互いに密接に関係している. 向きづけられた3次元閉リーマン多様体Mの -不変量は,M.F.Atiyah,V.K.Patodi,I.M.Singerの三氏により,自己共役な楕円型微分作用素のスペクトルを用いて定義された.彼らの主結果から,この不変量はMを境界としてもつ4次元コンパクトリーマン多様体Wにヒルツェブルフ符号数定理を適用した際の補正項として解釈することができる.つまり,P1をリーマン計量の第1ポントリャーギン形式,SignWをWの符号数としたときに -不変量は,M.F.Atiyah,V.K.Patodi,I.M.Singerの三氏により,自己共役な楕円型微分作用素のスペクトルを用いて定義された.彼らの主結果から,この不変量はMを境界としてもつ4次元コンパクトリーマン多様体Wにヒルツェブルフ符号数定理を適用した際の補正項として解釈することができる.つまり,P1をリーマン計量の第1ポントリャーギン形式,SignWをWの符号数としたときに  が成立する.従って,我々は定義からの直接計算が非常に困難である -不変量の計算を解析的手段を必要とせずに実行できるようになったのである.しかしながら,定義における計量の任意性から,一般に -不変量の計算を解析的手段を必要とせずに実行できるようになったのである.しかしながら,定義における計量の任意性から,一般に -不変量の計算は依然として難しく,特定の多様体に対する定式化も興味深い問題として捉えられてきた. -不変量の計算は依然として難しく,特定の多様体に対する定式化も興味深い問題として捉えられてきた. そこで我々の研究対象として,3次元多様体の構成法としてよく知られたうちの一つであるS1上の曲面束を考えることにする.特にモノドロミー写像が周期的の場合には,R.MeyerhoffとD.RubermanによりG-指数定理を用いてその -不変量の値が計算されている.また,M.Ouyangによるザイフェルト多様体の -不変量の値が計算されている.また,M.Ouyangによるザイフェルト多様体の -不変量の定式化の一部としてもその明示公式を得ることができる.これらの結果は,いずれもモノドロミー写像の固定点の情報から -不変量の定式化の一部としてもその明示公式を得ることができる.これらの結果は,いずれもモノドロミー写像の固定点の情報から -不変量を計算するものであるが,これと本質的に異なる定式化を与えるのが第一章前半部の結果である.これを詳しく述べよう.まず初めに,3次元閉リーマン多様体の有限被覆に対して,その全空間及び底空間の -不変量を計算するものであるが,これと本質的に異なる定式化を与えるのが第一章前半部の結果である.これを詳しく述べよう.まず初めに,3次元閉リーマン多様体の有限被覆に対して,その全空間及び底空間の -不変量の重複度からのずれの幾何学的解釈を与える.具体的にはAtiyahの標準2枠の概念を用いることにより,底空間の標準2枠を全空間にリフトして得られる2枠と全空間自身の標準2枠との差によって -不変量の重複度からのずれの幾何学的解釈を与える.具体的にはAtiyahの標準2枠の概念を用いることにより,底空間の標準2枠を全空間にリフトして得られる2枠と全空間自身の標準2枠との差によって -不変量の差を記述する.特に,周期的自己同型に対応する曲面束に対しては,この2枠の差を曲面の写像類群 -不変量の差を記述する.特に,周期的自己同型に対応する曲面束に対しては,この2枠の差を曲面の写像類群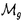 のある中心拡大に対応した2-双対輪体の有限和により具体的に記述することができる.結果として,曲面へのモノドロミー作用が等長的となる計量とS1の標準計量との積計量から誘導される計量に関するS1上の曲面束の のある中心拡大に対応した2-双対輪体の有限和により具体的に記述することができる.結果として,曲面へのモノドロミー作用が等長的となる計量とS1の標準計量との積計量から誘導される計量に関するS1上の曲面束の -不変量の定式化が得られるのである.先の2-双対輪体が本質的には符号数双対輪体 -不変量の定式化が得られるのである.先の2-双対輪体が本質的には符号数双対輪体 gに(正確には,定数倍を除いて)等しいという事実を考え併せると,この公式により,周期的自己同型に対応する曲面束の gに(正確には,定数倍を除いて)等しいという事実を考え併せると,この公式により,周期的自己同型に対応する曲面束の -不変量は,ファイバーのホモロジーへの作用から決まることがわかる. -不変量は,ファイバーのホモロジーへの作用から決まることがわかる. さて,コンパクト有向曲面の写像類は,Nielsen-Thurstonの理論により以下の三つのタイプに分類されることが知られている:(i)周期的,(ii)可約,(iii)擬アノゾフ.容易にわかるように(i),(ii)の写像類には共通部分がある.実際これまでに周期的自己同型の可約性の特徴づけに関するいくつかの結果が得られている.例えば,J.Gilmanにより考察された周期的写像類の作用による商軌道体の位相型を用いた特徴づけや,笠原泰氏による可約性の位数による特徴づけなどが知られている.本論文における我々の視点では,曲面の種数が低い場合には先の意味での -不変量(以下,周期的自己同型の -不変量(以下,周期的自己同型の -不変量と呼ぶ)が周期的写像類の可約性を完全に反映していることを主張する.以上第一章の結果をまとめると次の定理を得る. -不変量と呼ぶ)が周期的写像類の可約性を完全に反映していることを主張する.以上第一章の結果をまとめると次の定理を得る. 定理1:位数mの周期的自己同型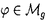 に対応する曲面束 に対応する曲面束 の の -不変量は,以下の表示をもつ -不変量は,以下の表示をもつ  ここで, は写像類群の古典的表現で, は写像類群の古典的表現で, はMeyerの符号数双対輪体である.特に曲面の種数が1,2のとき, はMeyerの符号数双対輪体である.特に曲面の種数が1,2のとき, が可約写像類である必要十分条件は, が可約写像類である必要十分条件は, で与えられる. で与えられる. 定理1の後半部分の主張は,クライン曲線と呼ばれる種数3のリーマン面の自己同型群 に対しても成立する.従って,周期的自己同型の に対しても成立する.従って,周期的自己同型の -不変量が曲面の写像類の複雑さを反映するという新たな見地が得られたのである. -不変量が曲面の写像類の複雑さを反映するという新たな見地が得られたのである. 次に,曲面の超楕円的写像類群(つまり,超楕円的対合 gと可換な写像類からなる gと可換な写像類からなる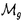 の部分群) の部分群)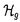 のMeyer関数について考えよう.これは以下のように定義される のMeyer関数について考えよう.これは以下のように定義される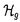 の有理1-双対鎖のことである. の有理1-双対鎖のことである.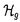 の2次のコホモロジー群が有限巡回群であることから,符号数双対輪体 の2次のコホモロジー群が有限巡回群であることから,符号数双対輪体 gによって表されるコホモロジー類は gによって表されるコホモロジー類は において有限位数をもつ.それ故, において有限位数をもつ.それ故,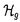 のある有理1-双対鎖 のある有理1-双対鎖 でその境界がちょうど符号数双対輪体 でその境界がちょうど符号数双対輪体 gになるもの gになるもの が存在する. が存在する.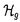 のアーベル化が再び有限巡回群であることから,この1-双対鎖dgは唯一つ定まり,これを種数gのMeyer関数とよぶ.以上のことは幾何学的には,曲面上の曲面束で対応するホロノミー準同型 のアーベル化が再び有限巡回群であることから,この1-双対鎖dgは唯一つ定まり,これを種数gのMeyer関数とよぶ.以上のことは幾何学的には,曲面上の曲面束で対応するホロノミー準同型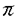 1(底空間)→ 1(底空間)→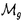 の像が,超楕円的写像類群 の像が,超楕円的写像類群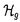 に含まれるものの符号数が常に消えることに対応している. に含まれるものの符号数が常に消えることに対応している. 種数が1のときには,Meyer自身によりRademacher関数 等を用いたd1の明示公式が与えられている.より具体的には, 等を用いたd1の明示公式が与えられている.より具体的には, に対して に対して  と記述される.ここで, である.その後,Atiyahによるd1の幾何学的解釈,Kirby-Melvinによる である.その後,Atiyahによるd1の幾何学的解釈,Kirby-Melvinによる 1の明示公式やSczechによるd1の純代数的手法を用いた記述が得られている.そこで次に考えるべき問題はd2の明示公式を与えることであるが,これは今もって解決されていない.その困難の本質は,種数が2以上のときには先の表現 1の明示公式やSczechによるd1の純代数的手法を用いた記述が得られている.そこで次に考えるべき問題はd2の明示公式を与えることであるが,これは今もって解決されていない.その困難の本質は,種数が2以上のときには先の表現 gがトレリー群と呼ばれる非常に大きな核をもつことに起因する.つまり,Sp-表現の下で失われるトレリー群上の情報をいかにして抽出するかが問題解決のポイントとなる.第二章の主結果は,以下で定義される gがトレリー群と呼ばれる非常に大きな核をもつことに起因する.つまり,Sp-表現の下で失われるトレリー群上の情報をいかにして抽出するかが問題解決のポイントとなる.第二章の主結果は,以下で定義される の部分群 の部分群 上これが実現できることを主張する.SL(2;Z)×SL(2;Z)の中心拡大 上これが実現できることを主張する.SL(2;Z)×SL(2;Z)の中心拡大  を考える.ここで,核Zはトレリー群 の正規生成元 の正規生成元 0により生成される.このとき, 0により生成される.このとき, 定理2: の部分群 の部分群 上,種数2のMeyer関数は以下の表示をもつ. 上,種数2のMeyer関数は以下の表示をもつ.  ここで, はアーベル化準同型,d1は種数1のMeyer関数である. はアーベル化準同型,d1は種数1のMeyer関数である. この定式化において,トレリー群 の軸となる正規生成元 の軸となる正規生成元 0の情報をアーベル化準同型という極めて基本的な関数によって抽出している点を強調したい.また,この明示公式からもMeyer関数がトレリー群上準同型になるという基本的事実を見て取れることに注意する. 0の情報をアーベル化準同型という極めて基本的な関数によって抽出している点を強調したい.また,この明示公式からもMeyer関数がトレリー群上準同型になるという基本的事実を見て取れることに注意する. これまで述べてきたように,3次元多様体の -不変量は幾何学的不変量(つまり,幾何構造に付随した不変量)であり,超楕円的写像類群のMeyer関数は群コホモロジー論的に定義される.これら二つの対象は(曲面の周期的自己同型に話を限ると),S1上の曲面束を通して結実する. -不変量は幾何学的不変量(つまり,幾何構造に付随した不変量)であり,超楕円的写像類群のMeyer関数は群コホモロジー論的に定義される.これら二つの対象は(曲面の周期的自己同型に話を限ると),S1上の曲面束を通して結実する. 定理3:種数gの超楕円的写像類群の周期的自己同型 に対して に対して 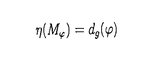 が成り立つ. これによって我々は,周期的自己同型の -不変量の位相的な記述を得るとともに,Meyer関数の一つの幾何学的意味づけを与えたことになる. -不変量の位相的な記述を得るとともに,Meyer関数の一つの幾何学的意味づけを与えたことになる. |
| 審査要旨 | | 本論文は,Meyer’s function, -invariants and the signature cocycle(Meyer関数, -invariants and the signature cocycle(Meyer関数, -不変量と符号数双対輪体)と題されており,全体で2章8節から成っている.その主題は,円周上の曲面バンドルという構造をもつ3次元Riemann多様体のエータ不変量と,曲面の写像類群の構造との関係の詳細な追求である.以下,得られている結果を章ごとに吟味する. -不変量と符号数双対輪体)と題されており,全体で2章8節から成っている.その主題は,円周上の曲面バンドルという構造をもつ3次元Riemann多様体のエータ不変量と,曲面の写像類群の構造との関係の詳細な追求である.以下,得られている結果を章ごとに吟味する. 第1章はVanishing thorems for the  -invariantと題されている.まず第1節では,位数が有限となるような曲面の微分同相写像の写像類による写像トーラスが考察され,そのような多様体上の許容される自然な計量に関するエータ不変量を,写像類群上のMeyerの符号数コサイクルと呼ばれる2-コサイクルによって完全に記述する公式(定理1.5)が与えられている.そして具体的な例として,任意種数の超楕円対合の場合と,種数1の場合の双方について,これまでに知られている結果がこの公式から統一的に得られることが確認されている.さらに,種数2で位数5および10の興味深い例についての計算結果が与えられており,高い種数の場合にも同様の実例が構成できることが示されている. -invariantと題されている.まず第1節では,位数が有限となるような曲面の微分同相写像の写像類による写像トーラスが考察され,そのような多様体上の許容される自然な計量に関するエータ不変量を,写像類群上のMeyerの符号数コサイクルと呼ばれる2-コサイクルによって完全に記述する公式(定理1.5)が与えられている.そして具体的な例として,任意種数の超楕円対合の場合と,種数1の場合の双方について,これまでに知られている結果がこの公式から統一的に得られることが確認されている.さらに,種数2で位数5および10の興味深い例についての計算結果が与えられており,高い種数の場合にも同様の実例が構成できることが示されている. 第2節と第3節では,曲面の有限位数の写像類のThurstonの意味での分類と,その写像トーラスのエータ不変量との相互関係が調べられている.種数2では,その関係は極めて簡明なものである.すなわち有限位数の写像類がreducibleになることと,その写像トーラスのエータ不変量が消えることが等価であることが証明されている(定理2.6).また種数3についても,部分的ではあるが同様の結果(定理3.1)が成立することが示されている. 第2章はMeye’s function of hyperelliptic mapping class groupsと題されている. 前述のMeyerの符号数コサイクルは種数1,2のとき,あるいは一般種数でも超楕円的な写像類全体のつくる写像類群の部分群(超楕円的写像類群と呼ばれる)上では,コバウンダリーとなることが知られている.したがって,これらの場合,対応する(超楕円的)写像類群上で定義される1コチェインが存在して,そのコバウンダリーがMeyerのコサイクルとなる.さらに(超楕円的)写像類群はすべてそのアーベル化が有限群となるため,これらの1コチェインは唯一通りに定まることになる.種数が1の場合には,Mayerがこの1コチェインを具体的に決定しているが,その背景には上半平面に働く不連続群としての種数1の写像類群の,トポロジーのみならず,整数論,複素関数論あるいは大域解析学といった数学のいろいろな分野の相互作用が現われており,極めて豊富な内容をもつものとなっている.これらの事柄を種数が高い場合に様々に拡張することは,大きな未解決問題となっている. さて,第2章の内容を簡明に要約すると,種数2の場合のこの問題に対する解答への着実な第一歩を印したということができる.第1節でMeyerの仕事を概観し,さらに第2,3節で技術的な準備をした後,第4節で種数2の写像類群のある重要な部分群上で上記の1コチェインを完全に記述する公式(命題4.1および系4.2)が与えられている.またその公式の一般の種数の超楕円的写像類群上へのある拡張(定理4.6)が述べられている. 最後に第5節では,ふたたび写像トーラスのエータ不変量と上記の1コチェインとの関係が考察され,任意の有限位数の超楕円的写像類上のこの1コチェインの値が,対応する写像トーラスのエータ不変量に一致するという美しい結果(定理5.1)が提示されている.この結果は,この両者の間に極めて深い関係があることを強く示唆するものとなっている. 以上のことから,論文提出者森藤孝之は,博士(数理科学)の学位を受けるにふさわしい充分な資格があるものと認める. |