| 内容要旨 | | 0.kを代数体とする.その絶対Galois群Gal(ksep/k)をGkで表す.Xをk上の非特異完備かつ絶対連結な多様体とする.lを素数,i及びnをi≠2nなる正の整数とする.l進regulator写像(論文§1(1.3)(1.6)参照)  は数論幾何における中心的な研究対象の一つである.ここで左辺はBeilinson[Be2]のモチビックコホモロジーで,代数的K群[Q]のAdams作用素[So2]による分解として定義される(論文§1(1.2)参照). Beilinson[Be1]に従い,Jannsenはi nの場合に写像 nの場合に写像 が単射であることを予想し,詳しい考察を与えている[J2,§2Conjecture2][J3,§13].この予想は混合モチーフの哲学[Be3][B]及びDeligne予想([J3,11.4]参照)の上に成り立っている.即ち,Spec Z上有限型なスキームに対する実現関手が忠実([J3,11.6]参照),かつ代数体k上には非自明なmotivic2-extensionが存在しない,という二つの予想の帰結である. が単射であることを予想し,詳しい考察を与えている[J2,§2Conjecture2][J3,§13].この予想は混合モチーフの哲学[Be3][B]及びDeligne予想([J3,11.4]参照)の上に成り立っている.即ち,Spec Z上有限型なスキームに対する実現関手が忠実([J3,11.6]参照),かつ代数体k上には非自明なmotivic2-extensionが存在しない,という二つの予想の帰結である. 本論文ではi=n+1かつn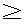 2の場合に写像 2の場合に写像 の単射性を扱う.この場合,写像 の単射性を扱う.この場合,写像 の単射性は の単射性は  という群の有限性と深く関わっている.ここでN・はconiveau filtration(論文§1(1.4)参照),F・は被覆 に関するHochschild-Serre filtrationである(論文§3(3.1)参照).添え字’div’は最大可除部分群を表す.実際n に関するHochschild-Serre filtrationである(論文§3(3.1)参照).添え字’div’は最大可除部分群を表す.実際n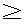 3の場合,いくつかの一般的な予想の下では写像 3の場合,いくつかの一般的な予想の下では写像 が単射であることと群 が単射であることと群 が非自明な可除部分群を含まないことが同値である(論文§1(1.6)Corollary1.2参照). が非自明な可除部分群を含まないことが同値である(論文§1(1.6)Corollary1.2参照). 1.主結果を述べる為,記号を正確に導入する.kを体とし,Xをk上の非特異完備かつ絶対連結な多様体とする.nを正の整数とし,  と置く.ここでrはkで可逆な全ての正の整数を走り,各rに対し rは1のr乗根のなすX上のエタール層を表す.Hn+1(X)の部分群 rは1のr乗根のなすX上のエタール層を表す.Hn+1(X)の部分群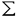 n(X)を n(X)を  と定義する.ここでN・及びF・は定義式(0.2)におけるそれらと同じである(論文§3(3.1)参照).この群のl準素部分が群 (0.2)に他ならない.次の場合を考える. (0.2)に他ならない.次の場合を考える. ―kが大域体,即ち,代数体又は有限体上の1変数関数体. ―kが局所体,即ち,大域体のある非アルキメデス素点での完備化. 主結果は次の通りである. 定理0.1(論文§4Theorem4.1).kを局所体,Xは上の通りとし,n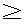 2とする.このとき群 2とする.このとき群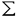 n(X)は有限である. n(X)は有限である. この結果はn=2の場合にはSalberger[Sal]によって既に示されている([Sat]参照).従って主結果はこの事実のn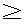 3の場合への拡張である. 3の場合への拡張である. JannsenのHasse原理[J2,Theorem3]及びこの主結果によって,次を得る. 系0.2(論文§3).kを代数体,Xは上の通りとし,n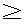 2とする.このとき群 2とする.このとき群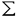 n(X)は有限である. n(X)は有限である. 2.次に主結果の応用を述べる.kを有限体上の1変数関数体,Xをk上の非特異完備かつ絶対連結な多様体とする.lをkで可逆な素数とする.ここではregulator写像[So1](論文§1(1.3)参照)  を考える.ここで右辺は連続エタールコホモロジーである[J1].このコホモロジーの,被覆 に関するHochschild-Serre filtrationをF・で表す. に関するHochschild-Serre filtrationをF・で表す. 定理0.3(論文§6Corollary6.4).k及びXを上の通りとし,n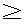 2とする.このとき, 2とする.このとき,  この結果はRaskindの最近の結果[Ra]のK群的な意味での一つの高次化である.彼は0サイクルのサイクル写像[J1,(6.14)]  に対して次を示している. 定理0.4(Raskind[Ra,Theorem 0.1]).k及びXを上の通りとする.このとき,  この事実及び上のTheorem0.3は共にregulator写像 (0.1)の単射性を期待する根拠となるであろう([J3,12.18]参照).Theorem0.3の証明ではRaskindの議論[Ra,Proposition3.6]を用いる.その際,JannsenのHasse原理[J2,§6Theorem4]及び主結果Theorem0.1が重要な役割を果たす(論文§6Theorem6.5参照). (0.1)の単射性を期待する根拠となるであろう([J3,12.18]参照).Theorem0.3の証明ではRaskindの議論[Ra,Proposition3.6]を用いる.その際,JannsenのHasse原理[J2,§6Theorem4]及び主結果Theorem0.1が重要な役割を果たす(論文§6Theorem6.5参照). さらにTheorem0.3の帰結を述べる.  と置く.Merkur’ev-Suslinの定理[MS]及びTheorem0.3から次を示すことができる. 系0.5(論文§6Corollary6.7).k及びXを上の通りとする.このとき,  但し添え字’l-div’は最大l可除部分群を表す. 3.最後にTheorem0.1の証明の概略を述べる.本質的な問題はXが局所体k上potentially good reductionを持たない場合にあり,de Jongの結果[dJ,Theorem6.5]を用いてXがstrictly semi-stable reduction(§2(2.4))を持つ場合にまで問題を帰着させる(論文§4(4.1)参照).kの剰余体の標数をpであらわす.素数lがpと素な場合は,エタールコホモロジー 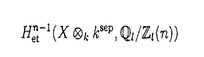 にweight filtrationを与え,その各部分商を,Rapoport-Zinkの結果[RZ,Satz2.21,2.23],Weil予想[D],及びGabberの結果[Ga]を用いて計算する.この計算により群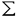 n(X)のl準素部分 n(X)のl準素部分 は見通し良く評価することができる.実際, は見通し良く評価することができる.実際, は殆ど全てのl≠pに対して自明であることがわかる(論文§4). は殆ど全てのl≠pに対して自明であることがわかる(論文§4). kがp進体でかつl=pである場合はl≠pの場合の類似を辿る.即ち,上のエタールコホモロジーを同様にして,Fontaine-Jannsen予想[HK][K][Ts],Mokraneのweightスペクトル系列[Mo],及びKatz-Messingの結果[KzM]を用いて計算する(論文§5). REFERENCES[Be1]Beilinson,A.:Higher regulators and values of L-functions.J.Soviet Math.30 2036-2070(1985)[Be2]Beilinson,A.:Notes on absolute Hodge cohomology.In:Bloch,S.J.,Dennis,R.K.,Friedlander,E.M.,Stein,M.R.(eds.)Applications of Algebraic K-Theory to Algebraic Geometry and Number Theory.(Contemp.Math.Vol.55 Part I,pp.35-68)Providence:American Mathematical Society 1986[Be3]Beilinson,A.:Height pairings between algebraic cycles.In:Manin,Yu.I.(ed.)K-Theory.Arithmetic,and Geometry.(LNM Vol.1289 pp.1-26)Berlin Heidelberg New York:Springer-Verlag 1987[B] Bloch,S.:Algebraic K-theory,motives,and algebraic cycles.In:Proc.of I.C.M.Kyoto,1990,43-54[D] Deligne,P.:La conjecture de Weil I.Publ.Math.,Inst.Hautes Etud.Sci.43,273-308(1974)[Ga] Gabber,O.:Sur la torsion dans la cohomologie l-adique d’une variete.C.R.Acad.Sc.Paris Serie I 297,179-182(1983)[HK] Hyodo,O.,Kato,K.:Semi-stable reduction and crystalline cohomology with logarithmic poles.In:Periodes p-adiques.Seminaire de Bures,1988.(Asterisque 223,pp.221-268):Societe Mathematique de France 1994[J1] Jannsen,U.:Continuous etale cohomology.Math.Ann.280,207-245(1988)[J2] Jannsen,U.:On l-adic cohomology of varieties over number fields and its Galois cohomology.In:Ihara,Y.,Ribet,K.A.,Serre,J.-P.(eds.)Galois Group over Q.Berlin Heidelberg New York:Springer-Verlag 1989[J3] Jannsen,U.:Mixed motives and algebraic K-theory.LNM 1400,Berlin Heidelberg New York:Springer-Verlag 1990[dJ] de Jone,A.J.:Smoothness,semi-stability,and alterations.Publ.Math.,Inst.Hautes Etud.Sci.85,51-93(1996)[K] Kato,K.:Semi-stable reduction and p-adic etale cohomology.In:Periodes p-adiques.Seminaire de Bures,1988.(Asterisque 223,pp.269-293):Societe Mathematique de France 1994[KzM]Katz,N.,Messing,W.:Some consequences of the Riemann hypothesis for varieties over finite fields.Invent.Math.23,93-97(1974)[MS] Merkur’ev,A.S.,Suslin,A.A.:K-cohomology of Severi-Brauer varieties and the norm residue homomorphism.Math.USSR Izv.21,307-341(1983)[Mo] Mokrane,A.: La suite spectrale des poids en cohomologie de Hyodo-Kato.Duke Math.J.72,301-337(1993)[Q] Quillen,D.:Higher algebraic K-theory I.In: Bass,H.(ed.)Algebraic K-theory I.(LNM vol.341 pp.85-147)Berlin Heidelberg New York: Springer-Verlag1973[RZ] Rapoport,M.,Zink,T.:Ueber die lokale Zetafunktion von Shimuravarietaten.Monodromiefiltration und verschwindende Zyklen in ungleicher Charakteristik.Invent.Math.68,21-101(1982)[Ra] Raskind,W.:Higher l-adic Abel-Jacobi mappings and filtraions on Chow groups.Duke Math.J.78,33-57(1995)[Sal]Salberger,P.:Torsion cycles of codimension two and l-adic realizations of motivic cohomology.In:S.David(ed.)Seminaire de Theorie des Nombres 1991/92 Boston:Birkhauser 1993[Sat]Sato,K.:Injectivity of the torsion cycle map of codimension two of varieties over p-adic fields with semi-stable reduction.preprint[So1]Soule,C.:Operations on etale K-theory.Applications.In:Dennis,R.K.(ed.)Algedraic K-theory,Oberwolfach 1980,Part I.(LNM vol.996 pp.271-303)Berlin Heidelberg New York:Springer-Verlag 1982[So2]Soule,C.:Operations en K-theorie algebrique.Canad.J.Math.37,488-550(1985)[Ts] Tsuji,T.:p-adic etale cohomology and crystalline cohomology in the semi-stable reduction case.preprint |
| 審査要旨 | | 提出論文における中心的な研究テーマはregulator写像 である。ここでXは代数体k上の射影的非特異代数多様体である。左辺はXの代数的K-理論により定義され、右辺はのエタールコホモロジーへのkの絶対ガロア群Gkの作用によるガロアコホモロジーである。regulator写像はXに付随する定義の全く異なるふたつの重要な不変量を関係づける写像で、現代の数論幾何学において最も盛んに研究されている対象のひとつである。regulator写像に関して次の予想がある。 予想 i<2nの時 は単射である。 は単射である。 この予想の背景にはBeilinsonの提出した混合モチーフの哲学とDeligneによる代数体上の混合モチーフの圏においては自明でない2-extensionが存在しないであろうという予想がある。これらの見地よりregulator写像の単射性が予想されるのである。Jannsenはi nの場合の nの場合の の単射性に関し詳しい考察を与えている。 の単射性に関し詳しい考察を与えている。 一方、この論文での実際の研究対象は具体的に以下のように定義される群である。 ここでNとFはXのエタールコホモロジー上に定義されるふたつの異なるフィルター付である.前者はconiveauフィルターとよばれる,幾何的なフィルター付でありXの部分スキームの局所コホモロジーより生ずる。後者はHochschild-Serreスペクトラル系列 より生じる,数論的なフィルター付である。またアーベル群MにたいしMdivでMの最大なdivisibleな部分群を表す。この論文ではまず の有限性のJannsenが扱わなかったi=n+1の場合のregulator写像 の有限性のJannsenが扱わなかったi=n+1の場合のregulator写像 の単射性との深い関わりが指摘されている.実際に次が示されている。 の単射性との深い関わりが指摘されている.実際に次が示されている。 命題1 次を仮定する。 このとき この命題の意味するところは の有限性がモチヴィック複体の存在の仮定のもとに の有限性がモチヴィック複体の存在の仮定のもとに の単射性のかなりの部分を導く力を持つということである。 の単射性のかなりの部分を導く力を持つということである。 さてこの論文における主結果は以下の通りである。 定理2X/kを前の通りとしn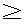 2と仮定する。このとき 2と仮定する。このとき は有限である。さらに殆ど全ての素数lにたいし成り立つ。 は有限である。さらに殆ど全ての素数lにたいし成り立つ。 この結果は の単射性のみならず実際上の応用が多々ある。 の単射性のみならず実際上の応用が多々ある。 この結果のn=2の場合はSalbergerの示した定理である.ただしSalbergerの証明は高次元類体論(局所体上の曲線の類体論)を使うが佐藤氏はこれを-p-進Hodge理論に置き換えた別証を与えている.Salbergerの定理は,Colliot-TheleneとRaskindによる次の定理の証明の重要な鍵となったのであった。 定理(Colliot-Thelene,Raskind)Xが代数体上の非特異かつ射影的な多様体で、H2(X,0とすると余次元2のChow群のねじれ部分CH2(X)torは有限アーベル群ある。 このChow群の有限性の問題はモーデル-ヴェイユの定理(代数体上のアーベル多様体の有理点のなす群は有限生成であるといる定理)の一般化ともいえる、数論幾何における重要問題である.Salbergerの定理の拡張である上の定理2がこの問題の進展に貢献することが期待される。 また定理2は次の興味深い結果を導く。 定理3kが有限体上の一変数関数体とし、Xをk上の射影的非特異な多様体とする。regulator写像 (ただしl≠ch(l))にたいしが成り立つ。 この事実も混合モチーフの哲学より予想されていたことであるが、これを何の予想も仮定せずに導いたことは注目に値する。 以下、簡単に定理2の証明の概略を述べる。まずJannsenのコホモロジー的Hasse原理により問題は局所体k上の代数多様体Xにたいする同様な主張に帰着される。次にde Jongのalteration定理によりXがsemi-stable reductionを持つ場合に帰着する。ここでlがkの剰余体の標数と異なる場合はRapoport-Zinkの結果を使いvanishing cycleの計算を行い定理が証明される。この計算は大変複雑で、論文の技術的な主要部分である。lがkの剰余体の標数に一致する場合はRapoport-Zinkの結果の代わりに、加藤-辻によって示されたp-進Hodge理論のFontaine-Jannsen予想を使って同様の計算を遂行する。 この論文で示された結果は現代の数論幾何学の中心的な問題に関わるものであり,その証明では数論幾何学の最先端の理論たちが活用されている。またこの結果は既に国際的にも高い評価を受けている.よって論文提出者佐藤周友は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. |