近年、非線形現象はより多くの研究者の興味を惹き付けている。「カオス」や「ソリトン」といった言葉はその様な方向の研究をあらわす良く知られたキーワードとなっている。

　19世紀中頃のJ.スコット-ラッセルによる発見の遥か後、1960年代におけるソリトンの再発見以来、そのソリトンという言葉でよく知られる非線形波動現象の研究は多方面に爆発的に拡がっている。それは、その現象が自然界に多く見られるからだけでなく、その背後のある深遠な数理的美が含まれているからである。

　その様な系の理論的研究の主要な一つの流れはその可解性に向けられた。非線形であるにも拘らず、あるのもは厳密に解かれたのである。現在ではその様な系のクラスは「可積分」と呼ばれ、その性質は「可積分性」と言われている。逆散乱法の成功の後、その理論的背景を探ったり、新たな応用を見つけたり、理論の進歩と拡張を行う努力が行われている。

　本論文で取り扱われる題材は1+1次元の、古典的(これは単に非量子論的であるという意味である)非線形力学系である。ここでの中心的な主題は「可積分性」である。そのような系の研究の拡張の幾つかの方向、すなわち離散化、境界値問題、多成分化といった事柄について述べる。

　序章において、ソリトン理論の発展とその拡張について概観する。また、本研究の動機について明らかにしたい。とくに、前半部における理論の並立性(parallelism)という興味ある観点-理論の殆どの部分が、連続系から半離散系(以下では「格子系」と呼ぶ、というのも空間部分の離散化のみを扱うからである)、離散系へ、非常に類似な形で適用可能であること-を、前半部への動機の一つとして、線形理論を例にとって触れた。

　本編の前半においては、可積分系の二つの重要な側面、即ち、保存則とベックルント変換について議論する。この前半部の全てにおいて、いづれも(上記の意味で)並立的である事が示されている。

　まずはじめに、一般化された補助線形問題(あるいは逆問題(IP)とも呼ばれる)を導入する。それはN次元ベクトルに対する二つの線形微分・差分方程式の組であり、「ラックス対」と呼ばれる一対のN×N行列、LとM(各々をL行列、M行列と呼ぶ)をもち、ある非線形力学系に付随するものである。これは連続時空系に対するM.J.アブロヴイッツらの2×2行列型(AKNS形式)の「逆散乱法」とM.J.アブロヴイッツとJ.F.ラディックによるその格子版(AL形式)の一つの拡張にあたる。このような一般化された枠組が「局所的」保存則

　を内在的に含む事を示す。これらは和達三樹らのAKNS系とそのある拡張にあたるKN系、WKI系に対する一連の結果を一般化したものであり、連続系だけでなく、格子系、離散系への系統的且つ実用的な保存量密度の生成法を与えた。2×2行列型での系での例を示した。

　次に、ベックルント変換(BT)について議論した。BTは一定の負曲率を持つ2次元曲面を記述するサイン-ゴルドン(SG)方程式の、曲面間の変換として1875年にA.V.ベックルントにより導入された。この変換は方程式の解の間の変換に相当し、これらからSG方程式の解の逐次的な構成-(その非線形性にも拘らず)解の重ね合わせ公式-が可能である。その後、ソリトン理論の発展に伴い、ベックルントの発見からほぼ100年後、コルテヴェグード・フリース(KdV)方程式のベックルント変換がH.D.ウァルキストとF.B.エスタブルックにより発見されると、多くの研究が他の可積分方程式へも行われ、変形KdV(mKdV)方程式、非線形シュレディンガー(NLS)方程式などでもBTが得られるとともに、その逆散乱法との関係も明らかにされた。1974年、H.-H.陳によりAKNS系の逆散乱法からこれらBTを系統的に導く手法が示された。ここでは、その手法がAL系にも適用できる事を示し、ロトカ-ヴォルテラ(LV)方程式s_n＝s_n(s_n+1-s_n-1)や変形LV(mLV)方程式、格子SG(LSG)方程式_n-_n-1＝sin(_n+_n-1)/2のBTの以下のような新しい表式を導出した(ここでは空間部分のみで時間部分は紙面の都合で省略。また、LV方程式については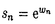、mLV方程式についてはq_n＝tan(_n+1-_n-1)/2というポテンシャル変数による表示である)。

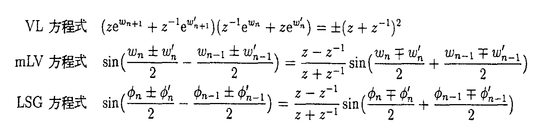　格子NLS(LNLS)方程式についてもその可能性を議論した。また、通常の議論と同様にこれらBTからLV、mLV、LSG、dSG方程式の解の重ね合わせ公式を導いた。さらに、同様の方法がdAKNS系でも適用可能な事を、離散SG(dSG)方程式を例にとって示した。

　後半部は近年盛んに研究されるソリトン理論の多岐にわたる拡張に関連した事柄についての研究結果を述べた。一つは境界値問題、もう一つは他成分化の問題に関連した事柄である。

　まず、境界値問題に関連した事柄を扱った。従来の理論例えば逆散乱法などは無限境界条件(無限遠でゼロとなるような境界条件)や周期的境界条件で解かれたり研究される事が殆どであった。しかし現実の系への応用を考えると、有限でより妥当な境界条件をもつ系を調べる事は非常に重要な課題である。この問題に一つの答えを与えたのがE.K.スクリヤーニンである。彼はハミルトン力学系のアプローチによって非線形可積分系を取り扱う古典r行列の手法を拡張する事で、可積分性を保つような境界条件を導入する手法を考案した。本研究では、ポアソン括弧に対して局所化されたL行列を使う事でスクリヤーニンのこのK行列の手法を用い有限N格子上のmLV方程式に次のような可積分境界条件を初めて導出した。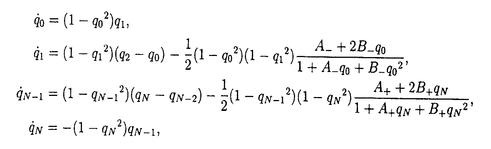

　議論においては、単純な有限化が物理的と期待される系を正しく導かない(可積分条件を満たすもの、両端間の相互作用を含んでしまう)事も示されている。

　次に、他成分化に関連する研究について述べた。ここでは一成分のNLS方程式を波動場から導出する際に用いられた、多重スケール摂動の方法を二成分系に適用した結果について述べた。充分一般的と考えられる非線形クライン-ゴルドン方程式から出発して二成分では次のような結合型NLS(cNLS)方程式を得た。

　しかしながら、一成分の場合と違い、これらが必ずしも可積分であるかどうかは自明でないが、これらがこれまでに知られている可積分なcNLSの幾つかを含む事が分かった。

　最後にこれらの研究の次の発展の可能性について簡単に記した。

　以上、本論文では古典的非線形可積分力学系とそれらに関連する系について研究を進め、逆散乱方を用いた保存則の構成法、AL系のベックルント変換及びそれを用いた解の重ね合わせ公式、K行列法による有限格子上のmLV方程式の可積分境界条件、二成分波動系における結合型NLS方程式と可積分性との関係を明らかにした。

　これらの成果と新たに得られた知見は現在も活発に進められている非線形可積分系の研究、ひいては非線形現象の基礎的な理解の更なる発展に寄与するものである。

　本論文は(1+1)-次元の、古典的非線形力学系の可積分性についての研究であり、その主題は、理論の離散化、境界値問題、多成分化といった拡張にある。以下その六章の各々について成果を要約する。

　第一章は導入である。古典ソリトン理論の歴史の簡単な要約に続いてこの論文全体に及ぶ一つのテーマである、格子化、離散化という問題を説明している。本論文では、可積分な微分方程式があった時、その空間変数を差分化した微分差分方程式を格子系と呼び、また更に時間変数まで差分化した方程式を離散系と呼んでいる。可積分性を維持したまま格子化や離散化が可能か、また連続理論で知られている様々な可積分系の性質をどこまで差分化できるかが前半の主題であることを簡単な例を用いて説明している。

　第二章では保存則について考察した。無限個の保存量の存在は可積分性の重要な必要条件である。まずはじめに、ラックス対と呼ばれる一対のN行N列による補助線形問題を導入し、その可積分条件がもとの非線型方程式となるよう設定する。特にN＝2の連続系はAKNS系、格子系はAL系と呼ばれる。このような一般化された系に対し、連続系だけでなく、格子系、離散系のそれぞれについて系統的且つ実用的な保存量密度の生成法を与えた。これは線形補助問題の「波動関数」の比がリッカチ型方程式をみたすことを利用するもので、それまでに知られていた結果を統合、拡張している。特にAL系及びdAKNS系についてはこの手法の初めての適用例であり、別の方法から知られていた保存量を再現する。

　第三章ではベックルント変換(BT)について議論した。BTとは可積分な方程式のいろいろな解を関係づけるものであり、それを用いて解の逐次的な構成を与えることが可能となる重要な変換である。本論文では、1974年にH.H-陳により連続系に対して開発された手法を差分版に拡張した。具体的にはAL系にも適用できる事を示し、ロトカ-ヴォルテラ(LV)方程式、変形ロトカ-ヴォルテラ(mLV)方程式、格子サインゴルドン(LSG)方程式のBTの新しい表式を導出した。格子非線形シュレディンガー方程式(LNLS)方程式についてもその可能性を議論した。また、これらBTからLV、mLV、LSG、dSG方程式の解の重ね合わせ公式を導いた。さらに、同様の方法がdAKNS系でも適用可能な事を、離散サインゴルドン(dSG)方程式を例にとって示した。これらの成果は第6章のTable 6.1にまとめられている。

　第四章では境界のある可積分方程式を扱った。従来の理論、例えば逆散乱法などにおいては無限系や周期的境界条件のもとでの研究が主体であった。これに関し、1987年、E.K.スクリヤーニンにより古典r行列の手法が拡張され、可積分性を保つような境界項を導入する手法が与えられた。本論文では、スクリヤーニンの手法を用いて有限N格子上のmLV方程式に対しポアソン可換なモノドロミー行列を構成した。その特殊値は境界項を含むmLV方程式のハミルトニアンになっており、結果として境界項付きの可積分な運動方程式を初めて導出することに成功した。ハミルトニアンは有限項からなり、境界項は四つの自由なパラメータを含むことから、これは現実の系への適用の可能性も期待される。

　第五章では非線形クラインゴルドン方程式の多成分化についての考察した。一成分系の場合は、多重スケール摂動という方法で解析すると、振幅の変調成分と呼ばれる量が可積分な非線形シュレディンガー方程式に従うことが知られていた。本論文では二成分非線形クライン-ゴルドン方程式から出発し、同様の解析を経て得られる結合型シュレディンガー方程式の一般形を初めて与えた。一成分の場合と違い、それが必ずしも可積分であるかどうかは不明であるが、少なくともそれまでに知られている可積分な結合型シュレディンガー方程式を幾つかを含む事を示した。

　第六章は結果の簡潔な要約と展望が述べられている。

　以上、本論文は古典的非線形可積分力学系とそれらに関連する系について、保存則の構成法、AL系のベックルント変換及びそれを用いた解の重ね合わせ公式、有限格子上のmLV方程式の可積分境界項、二成分波動系に関連した結合型NLS方程式の可積分性等について新たな結果と知見を与えるものである。

　なお、本論文の第三、四章は和達三樹氏と、第五章は和達三樹氏、土田隆之氏との共同研究に基づくものであるが、論文提出者が主体となって解析を進めたもので、論文提出者の寄与が十分であると判断する。

　以上により、審査委員会は、本論文が、学位論文として合格であり、学位申請者に博士(理学)の学位を授与しうるものと判断した。

　したがって博士(理学)の学位を授与できると認める。