| 内容要旨 | | 非圧縮流体の運動は、速度場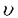 (x)の時間発展を記述するナヴィエ=ストークス(NS)方程式に支配される。 (x)の時間発展を記述するナヴィエ=ストークス(NS)方程式に支配される。  ここで、pは圧力、 は動粘性係数、fは外力である。場の代表的な速度と長さをそれぞれU,Lとすると、レイノルズ数Re=UL/ は動粘性係数、fは外力である。場の代表的な速度と長さをそれぞれU,Lとすると、レイノルズ数Re=UL/ が大きくなるほど、流体は複雑に乱れた「乱流」状態となる。支配方程式に基づく理論解析が非常に困難であるため、特に2点間距離が短いほど顕著になる速度差の非ガウス性(「間欠性」と呼ばれる)などを説明する理論は、現象論が中心となっている。 が大きくなるほど、流体は複雑に乱れた「乱流」状態となる。支配方程式に基づく理論解析が非常に困難であるため、特に2点間距離が短いほど顕著になる速度差の非ガウス性(「間欠性」と呼ばれる)などを説明する理論は、現象論が中心となっている。 その一方、近年の計算機の発達は、高レイノルズ数の乱流の直接数値シミュレーション(DNS)を可能にし、実験では不十分であった、瞬間場の3次元的な「構造」についての研究が盛んになされるようになった。特に、発達した乱流場中には、渦度 =▽× =▽×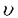 が細長く管状に集中した微細構造(これは通常「ワーム」と呼ばれる)が数多く存在していることが発見され、間欠性に対応する構造として注目されている。 が細長く管状に集中した微細構造(これは通常「ワーム」と呼ばれる)が数多く存在していることが発見され、間欠性に対応する構造として注目されている。 本研究では、粘性領域から慣性領域にかけての小スケールにおける乱流場の簡単なモデルとして、NS方程式の定常厳密解である「バーガース渦」が一様等方分布をする場の統計法則を研究した(その一部は[1]として発表している)。乱流場の小スケールの空間構造と統計法則の関係を明らかにすることを目的としている。局所的なダイナミクスをバーガース渦として取り入れており、単なる現象論に留まってはいない。 バーガース渦の速度場は、NS方程式(1)の定常解として、円柱座標系x=(r, ,z)において ,z)において  で与えられる[2]。ここでrB=(2 /a)1/2はバーガース半径、 /a)1/2はバーガース半径、 は渦の強さを表す全循環であり、渦度がz軸対称なガウス密度型 は渦の強さを表す全循環であり、渦度がz軸対称なガウス密度型 となる。この渦構造は、渦なし変形速度場 となる。この渦構造は、渦なし変形速度場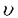 e(x)=(-ar,0,2az)の中に渦度場 e(x)=(-ar,0,2az)の中に渦度場 =(0,0, =(0,0, (r))が埋め込まれていて、径方向の粘性拡散と軸方向の強さ2aの引き伸ばしが平衡を保っている状態にある。また、この変形速度場中の、任意の軸対称渦度が漸近する解でもあることも示されている[2]。 (r))が埋め込まれていて、径方向の粘性拡散と軸方向の強さ2aの引き伸ばしが平衡を保っている状態にある。また、この変形速度場中の、任意の軸対称渦度が漸近する解でもあることも示されている[2]。 バーガース渦の等方分布は、渦度場が外部変形速度場よりも支配的である場合に(つまり渦近傍において)、両者が0ではない限り、乱流場の特徴の一つである負の歪み度を持つことが示される[1]。これが、ワームのモデルとしてバーガース渦を取り上げた主な理由であるが、実際に、ワーム構造はバーガース渦で良く近似できることが、DNS[3]や実験[4]による乱流場の解析で明らかにされている。 Townsendによる先駆的な研究[5]では、固定した循環と半径を持つランダムな向きのバーガース渦が、無限遠まで一様独立に分布すると仮定して、渦度による速度場に関して(渦なし変形場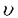 eを除外している)、波数kについてE(k)〜k-1となるエネルギー・スペクトルを導いた。これに対し、渦度場と渦なし変形場の混合が乱流場特有の統計法則を生み出すという考えに基づき、全速度場(2)に関する構造関数、すなわち差分距離l=|l|に対する縦速度差 eを除外している)、波数kについてE(k)〜k-1となるエネルギー・スペクトルを導いた。これに対し、渦度場と渦なし変形場の混合が乱流場特有の統計法則を生み出すという考えに基づき、全速度場(2)に関する構造関数、すなわち差分距離l=|l|に対する縦速度差 のモーメント のモーメント を、次の仮定の元で計算する(ここで、〈〉は統計平均をあらわしている)。 を、次の仮定の元で計算する(ここで、〈〉は統計平均をあらわしている)。 1.ランダムな渦軸の向き(等方性)。 2.渦軸までの距離r r0の有限球領域内での一様分布。 r0の有限球領域内での一様分布。 バーガース渦の持つ独立な2変数、半径rBと渦レイノルズ数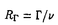 への依存性が残るが、慣性領域に対応する分数指数スケーリング への依存性が残るが、慣性領域に対応する分数指数スケーリング を示す領域がl>rBで存在し、 を示す領域がl>rBで存在し、 が大きいほどスケーリング指数 が大きいほどスケーリング指数 がコルモゴロフのスケーリング則 がコルモゴロフのスケーリング則 =p/3から下に離れていくことが明らかになった[1]。そこで =p/3から下に離れていくことが明らかになった[1]。そこで を確率変数とみて、DNS[3]や実験[4]による解析結果を参考に次の仮定を置く。 を確率変数とみて、DNS[3]や実験[4]による解析結果を参考に次の仮定を置く。 3. のガンマ分布。 のガンマ分布。 観測事実である、〈 〉∝ 〉∝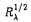 というテイラー微小スケール というテイラー微小スケール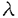 に基づくレイノルズ数 に基づくレイノルズ数 依存性と、rB 依存性と、rB O( O( )は、現象論的な考察によって示すことができる( )は、現象論的な考察によって示すことができる( はコルモゴロフの微小スケール)[1]。r積分の上限値がr0=2.5rB程度では、2次の2/3乗則や3次のコルモゴロフの4/5法則が満たされるが、r0を大きく取ると外部変形場が支配的となり、低次構造関数ではスケーリング領域が得られない。しかし、高次ではr0への依存性は弱く、DNSや実験を補外するような指数のスケーリングを示す(図1)。 はコルモゴロフの微小スケール)[1]。r積分の上限値がr0=2.5rB程度では、2次の2/3乗則や3次のコルモゴロフの4/5法則が満たされるが、r0を大きく取ると外部変形場が支配的となり、低次構造関数ではスケーリング領域が得られない。しかし、高次ではr0への依存性は弱く、DNSや実験を補外するような指数のスケーリングを示す(図1)。  図1:構造関数のスケーリング指数 図1:構造関数のスケーリング指数 バーガース渦がそれぞれ独立な一様分布をすると仮定すれば、その存在確率は考える領域の体積のみに依存したポアソン分布に従う。よって、2を修正して次のように精密化できる。 2’.渦軸までの球体積(4 /3)r3の指数分布。 /3)r3の指数分布。 ただし、rの期待値の外側で急速に減衰する分布なので、2からの本質的な変化は認められない。 縦速度差の構造関数はこのように慣性領域が認められるのに対して、横速度差では、対応する領域で負の傾きのスケーリングとなる。横は縦より間欠性が強いという乱流場の特徴を、定性的に示していることにはなるが、慣性領域を良く再現するモデルであるとはやはり言い難い。これは、渦度の強い渦構造を跨ぐ横速度差は非常に大きくなるため、本モデルが渦度の強く集中した領域のみをサンプルとしている以上、微小スケールでの横速度差を過大に評価していることになるからであると考えられる。そこで、最後に残ったバーガース渦の独立変数である半径rBを確率変数としてその分布を考慮してみる。 4.半径rBの対数正規分布。 半径分布をガンマ分布とした場合、本モデルではモーメントの積分が発散するために、対数正規分布とした。低温ヘリウムガスによる広範囲の高レイノルズ数を達成した室内乱流実験[4]では、ワーム構造の半径と回転方向の最大速度の確率分布は対数正規であると報告されており、DNS[3]でも同様のPDFが示されている。しかし、ガンマ分布と対数正規分布は密度の大きな部分でほぼ同形であり、両者の違いが現れる分布の裾の評価は、ワームの同定方法やサンプル数に強く依存し、観測ではどちらであるか断定出来ないと考えられる。半径や循環の分布は、ワームのダイナミクスを反映した確率過程との密接な関係が予想されるが、そのような確率モデルの構築は今後の課題となる。なお、3の の分布が対数正規である可能性もある訳だが、当モデルでは の分布が対数正規である可能性もある訳だが、当モデルでは に関しては2つの分布がほぼ同じ結果を与えることを確認した。 に関しては2つの分布がほぼ同じ結果を与えることを確認した。 以上の仮定により得られた、速度差のPDFを図2に示す(〈r〉=2.5(rB))。 が大きい場合ほど、慣性領域に入り込む距離まで乱流場の特徴を再現するモデルであるので、ここでは が大きい場合ほど、慣性領域に入り込む距離まで乱流場の特徴を再現するモデルであるので、ここでは =2000とおいた。 =2000とおいた。 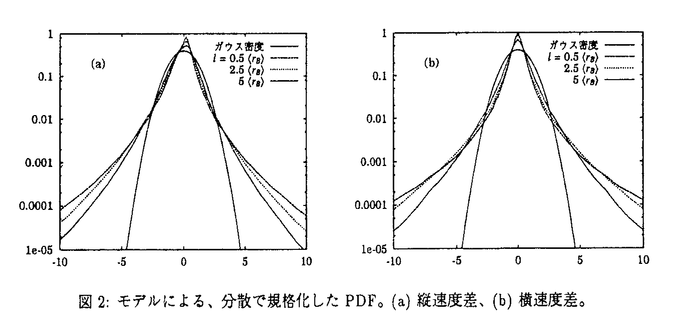 図2:モデルによる、分散で規格化したPDF。(a)縦速度差、(b)横速度差。 図2:モデルによる、分散で規格化したPDF。(a)縦速度差、(b)横速度差。 図3:減衰乱流DNSによる、分散で規格化したPDF。(a)縦速度差、(b)横速度差。 図3:減衰乱流DNSによる、分散で規格化したPDF。(a)縦速度差、(b)横速度差。 (i)差分距離lが小さいほど分布の裾が上がる。 (ii)縦速度差は負の歪み度を持つ非対称な分布となる。 (iii)横速度差は縦速度差より分布の裾が上がり強い間欠性を示す。 などの乱流場の特徴を良く捉えていることが分かる。比較のため、航空宇宙技術研究所の数値風洞(NWT)による減衰乱流DNSの、エネルギー散逸率がほぼ最大となる時刻での空間平均PDFを図3に示す( =120)。3つの距離はそれぞれ対応するようにとった。モデルのPDFは裾がDNSより上に出るが、これは =120)。3つの距離はそれぞれ対応するようにとった。モデルのPDFは裾がDNSより上に出るが、これは をDNSより大きくとったためであり、実験事実に矛盾しない結果である。 をDNSより大きくとったためであり、実験事実に矛盾しない結果である。 構造関数に関しては、2次の縦横ともに、 =2000では〈r〉=2.5〜4〈rB〉にとった場合に、ほぼ同じ指数(約0.7)の狭いスケーリング領域が存在することが明らかになった。ただし、l≫〈r〉ではrBを固定した場合と同様、高次になるほど横構造関数が負のスケーリングを示すようになる。横速度差の統計法則まで含めると、やはりこのモデルは、lが〈r〉程度までの渦の内部構造に対応したスケールにおいて、乱流場の微小スケールの間欠性を説明するモデルであると言える。 =2000では〈r〉=2.5〜4〈rB〉にとった場合に、ほぼ同じ指数(約0.7)の狭いスケーリング領域が存在することが明らかになった。ただし、l≫〈r〉ではrBを固定した場合と同様、高次になるほど横構造関数が負のスケーリングを示すようになる。横速度差の統計法則まで含めると、やはりこのモデルは、lが〈r〉程度までの渦の内部構造に対応したスケールにおいて、乱流場の微小スケールの間欠性を説明するモデルであると言える。 最後に本研究の結果をまとめる。乱流場中の微細渦構造をバーガース渦でモデル化することにより、局所ストレインを伴う微細渦構造が、粘性領域から慣性領域へと遷移するスケール以下での乱流場の間欠性と対応しており、それには渦の半径と循環の確率分布が強く影響しているということを、渦構造の一様等方独立性という妥当な仮定の元で示すことができた。縦速度差の構造関数では、実験やDNSに近い慣性領域での異常スケーリングが得られるが、横速度差は同等の慣性領域を持たない。これは、バーガース渦が無限遠まで一定ストレインの変形速度場中の漸近定常解であり、乱流場中のワーム構造は適当な時間スケールで生成消滅する非定常な渦構造であることを反映しないためであると考えられる。そのようなダイナミクスを反映した、半径や循環などの確率分布の形も説明し得るモデルの構築が、今後の課題である。 参考文献[1] N.Hatakeyama and T.Kambe,"Statistical laws of random strained vortices in turbulence,"Phys.Rev.Lett.79,1257(1997);"Statistical properties of random distribution of strained vortices in turbulence,"in Advances in Turbulence VII,edited by U.Frisch(Kluwer,1998),pp.339-342.[2]J.M.Burgers,"A mathematical model illustrating the theory of turbulence,"Adv.Appl.Mech.1,171(1948);T.Kambe,"Axisymmetric vortex solution of Navier-Stokes equation,"J.Phys.Soc.Jpn.53,13(1984).[3]J.Jimenez,A.A.Wray,P.G.Saffman and R.S.Rogallo,"The structure of intense vorticity in isotropic turbulence,"J.Fluid Mech.255,65(1993);J.Jimenez and A.A.Wray,"On the characteristics of vortex filaments in isotropic turbulence,"ibid.373,255(1998).[4]F.Belin,J.Maurer,P.Tabeling and H.Willaime,"Observation of intense filaments in fully diveloped turbulence,"J.Phys.H France 6,573(1996);F.Belin,F.Moisy,P.Tabeling and H.Willaime,"Worms in a turbulence experiment,from hot wire time series,"preprint(1998).[5]A.A.Townsend,"On the fine scale structure of turbulence,"Proc.R.Soc.Lond.A 208,534(1951). |
| 審査要旨 | | 乱流では流体が時間的空間的に不規則な運動をおこない、運動量やエネルギー、物質の輸送係数が層流に比べて非常に大きくなる。このような乱流の統計的性質を理解するために2点間の速度差が注目され考察されてきた。その確率密度分布がガウス分布からずれること、構造関数すなわち速度差の高次モーメントが異常スケーリングを示すことなどが知られている。一方、近年の計算機の発達により高レイノルズ数の乱流の直接数値計算(DNS)が可能になり、実験では不十分であった乱流の3次元的な構造について詳しく調べられ、発達した乱流場中に渦度が細長く管状に集中した微細構造(ワーム)が数多く存在すること、その構造が流体方程式の厳密解であるバーガース渦でよく近似できることがわかってきた。そこで本研究では乱流場のモデルとしてバーガース渦が一様等方分布をする場を仮定し統計法則を調べた。粘性領域から慣性領域にかけての小スケールにおける乱流場の空間構造と統計法則の関係を明らかにした。 まず第1章で研究の動機と背景を述べた後、第2章では乱流場のワーム構造について説明した。DNSの研究からワームの半径はコルモゴロフの散逸長さのオーダーで、周速度の最大値は乱流場の乱れ速度のオーダーであることが知られている。また実験でも気泡を使って低圧力部を可視化しバーガース渦に似た微細構造があることがわかっている。 第3章ではバーガース渦について説明した。バーガース渦では渦なし変形速度場の中に管状の渦が埋め込まれ、粘性による渦の拡散と外部変形速度場による渦の引き延ばしが平衡を保っている状態にある。渦の循環の強さと半径の二つが独立パラメータとなる。ワームのモデルとして渦管だけでなく外部変形速度場も考慮することが本研究の特徴の一つである。 第4章ではバーガース渦の速度分布を用いて任意の2点の速度差を求める式を導出した。渦を一様等方に分布させるかわりに、渦の位置を固定して速度差を求める2点の位置(片方を実験室系の原点とする)を変えて平均をとる。渦の座標系と実験室系のオイラー角について積分することが渦の等方分布に対応する。また渦の中心と実験室系の原点の位置が独立でありその距離がポアソン分布をとることが渦の一様分布に対応する。さらにバーガース渦の循環の強さと半径についても確率分布を導入した。 第5章では前章の式を積分することにより構造関数のスケーリング指数の分布を求め、統計性質を議論した。まず渦の循環の強さを固定した場合を考察した。渦の中心と原点との距離を最適化することにより、3次の構造関数がコルモゴロフの4/5則を満たすこと、またスケーリング指数の分布がコルモゴロフのスケーリング則より下に離れ、渦の循環が強いほどそれが顕著であることがわかった。次に渦の循環の強さに対する確率分布がガンマ分布であると仮定し積分することにより、高レイノルズ数の場合のスケーリング指数の分布と速度差の確率密度分布を求め、実験やDNSの結果とよく一致することを示した。さらに渦の中心と原点の距離に対する依存性を調べ、高次の構造関数については依存性が少ないことを示した。最後に渦の半径が対数正規分布であると仮定して積分を行い、速度差の確率密度分布を求めた。差分距離が小さいほど分布の裾が上がる、縦速度差は負の歪み度を持つ非対称な分布となる、横速度差は縦速度差より分布の裾が上がり強い間欠性を示すなど、乱流場の間欠的な特徴をよくとらえていることがわかった。 以上、本論文では乱流場の微細渦構造をバーガース渦でモデル化し構造関数のスケーリング指数や速度差の確率密度分布などの統計性質を考察した。小さいスケールすなわち短い差分距離に関する統計性質については、外部変形速度場を伴う微細渦構造が乱流の間欠的な性質をよく記述できることがわかった。乱流の微細構造と統計性質の直接の関係を示したこれらの成果は流体物理学に大きく貢献するものである。なお、本論文は神部勉氏との共同研究であるが、論文提出者が主体となって理論解析を行ったもので、論文提出者の寄与が十分であると判断する。 したがって、博士(理学)の学位を授与できると認める。 |