| 内容要旨 | | 本論文では多変量正規分布における 1.分散共分散行列の推定 2.平均ベクトルの縮小推定量の平均二乗誤差の推定. という二つの推定問題を取り上げ,そのそれぞれに関し新たな知見を得ている. 1.分散共分散行列の推定 以下のような多変量分散分析モデルを考える.  ここで,N(M,  Ik)は各Xiが独立にM=( Ik)は各Xiが独立にM=(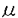 1,…, 1,…,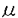 k)の対応する列ベクトル k)の対応する列ベクトル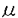 iを平均, iを平均, を分散共分散行列とする多変量正規分布に従うことをあらわす.Wp(n, を分散共分散行列とする多変量正規分布に従うことをあらわす.Wp(n, )は行列のサイズがp×p,自由度n,平均パラメータ )は行列のサイズがp×p,自由度n,平均パラメータ のウィシャート分布である.最小十分統計量は(X,S)で与えられ,これらは完備である.ここではMが未知の場合の のウィシャート分布である.最小十分統計量は(X,S)で与えられ,これらは完備である.ここではMが未知の場合の の推定を考える.損失関数としてはスタインの損失関数と呼ばれる の推定を考える.損失関数としてはスタインの損失関数と呼ばれる  を用いる.最小分散不偏推定量は自明に 0=S/nで与えられる.しかし 0=S/nで与えられる.しかし 0は非許容的であり,しかもp 0は非許容的であり,しかもp 2では損失関数(1)のもとミニマクスですらないことが知られている. 2では損失関数(1)のもとミニマクスですらないことが知られている. Sinha and Ghosh(1987)は以下のような推定量が 0を改良することを示した. 0を改良することを示した.  この推定量はいわばp=1の場合のStein(1964)の打ち切り型推定量の多変量版であるが,行列は全順序構造を持たないことから,このような打ち切り型の推定量は不連続になる.これは推定量としてはやや不自然なものである.実際シミュレーションによれば,改良は非常に小さい.k=1の場合,Perron(1990)はこの不連続性を修正した推定量を提案した.この推定量は を改良することが理論的に示されている上に,シミュレーションによると を改良することが理論的に示されている上に,シミュレーションによると 0に対する改良も 0に対する改良も に比べ顕著に大きい.しかし,Perronの結果はk=1という仮定に依存しており,彼の結果はk に比べ顕著に大きい.しかし,Perronの結果はk=1という仮定に依存しており,彼の結果はk 2へは直接拡張することができない. 2へは直接拡張することができない. 第二章では 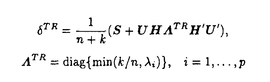 がk=1の場合にPerronの推定量に一致し,しかも一般にk 2においても 2においても を改良することを証明した.ここで,UはSの任意の行列平方根, を改良することを証明した.ここで,UはSの任意の行列平方根, i,Hの各列はU-1XX’U’-1のそれぞれ固有値,固有ベクトルであるとする.今,Wを確率密度関数がLebesgue測度dWに関し i,Hの各列はU-1XX’U’-1のそれぞれ固有値,固有ベクトルであるとする.今,Wを確率密度関数がLebesgue測度dWに関し  であるようなp×p確率変数行列とする. TRの TRの に対する改良は,Sinha and Ghosh(1987)の不等式 に対する改良は,Sinha and Ghosh(1987)の不等式  を用いて,(1)のW-1 の条件つき期待値,すなわち条件つきリスクを計算することによって証明される.シミュレーションを行った結果,改良は非常に大きいことがわかった. の条件つき期待値,すなわち条件つきリスクを計算することによって証明される.シミュレーションを行った結果,改良は非常に大きいことがわかった. 最小分散不偏推定量を改良するのにはミニマクス推定というもう一つのアプローチがある.Sのスペクトル分解を  であらわしたとき,  が 0を改良するミニマクス推定量になることをDey and Srinivasanは示した. 0を改良するミニマクス推定量になることをDey and Srinivasanは示した. DSも非許容的であることが知られており,実際,Sheena and Takemura(1992)らによって DSも非許容的であることが知られており,実際,Sheena and Takemura(1992)らによって DSを改良する推定量が導出されている.しかし,今まで提案されてきたミニマクス推定量はすべてSの情報のみを用いたものであった.そこで第三章では,Xの情報を用いた DSを改良する推定量が導出されている.しかし,今まで提案されてきたミニマクス推定量はすべてSの情報のみを用いたものであった.そこで第三章では,Xの情報を用いた ミニマクス推定を考え,Sの情報のみを用いたミニマクス推定量を改良する推定量を導出した.ここでは,U=QL1/2とおいて,先ほどと同様にW-1 ミニマクス推定を考え,Sの情報のみを用いたミニマクス推定量を改良する推定量を導出した.ここでは,U=QL1/2とおいて,先ほどと同様にW-1 の条件つきリスクを計算することにより,例えば, の条件つきリスクを計算することにより,例えば,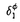 = =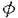 ( ( ) ) DS, DS, 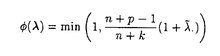 がk pにおいてDey-Srinivasanの推定量を改良することが証明される. pにおいてDey-Srinivasanの推定量を改良することが証明される. 第四章では,一元配置繰り返し数一定の多変量分散成分模型における分散成分の推定問題を取り上げた.モデルは以下のようなものである.  Xij,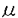 はp×1のそれぞれ観測値ベクトル,平均パラメータ(未知)である.また はp×1のそれぞれ観測値ベクトル,平均パラメータ(未知)である.また  を仮定する. e, e, vのUMVU推定量は完備十分統計量 vのUMVU推定量は完備十分統計量  を用いて,  と書ける.しかし, は正の確率で非負定行列以外をとるという欠陥がある.そこでその修正が必要になるが,確率1で非負定行列になるような推定量は過去にも提案されている. は正の確率で非負定行列以外をとるという欠陥がある.そこでその修正が必要になるが,確率1で非負定行列になるような推定量は過去にも提案されている. Amemiya(1985)はSe,Svのみに基づく尤度の最大化によって得られる  なる推定量を提案している.この推定量は eと eと e+n e+n vのみ( vのみ(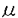 を無視)の尤度の最大化によって得られることから,制約付最尤推定量と呼ばれる.ここで,TはSe+Svのコレツキー分解によって得られる下三角行列, を無視)の尤度の最大化によって得られることから,制約付最尤推定量と呼ばれる.ここで,TはSe+Svのコレツキー分解によって得られる下三角行列, i,Pの各列はT-1SeT-1’のそれぞれ固有値,固有ベクトルである. i,Pの各列はT-1SeT-1’のそれぞれ固有値,固有ベクトルである. この推定量は確率1で非負定になる.しかしこの推定量は適当なリスクの下で,不偏推定量を改良するというような決定理論的な結果は得られていなかった.そこで第四章では,この問題を e, e, vの同時推定問題としてとらえ,損失関数 vの同時推定問題としてとらえ,損失関数 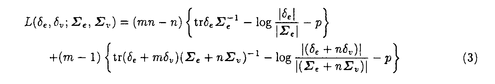 に対して, , ,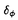 が不偏推定量を改良することを証明した. が不偏推定量を改良することを証明した. この推定量は形が先にのべた TRに対応しているので(2)に対応する不等式が得られれば条件つきリスクの計算によって証明ができることが予想される.しかしこの不等式の導出は困難と考えられてきた.Hをp×pの直交行列のなす群 TRに対応しているので(2)に対応する不等式が得られれば条件つきリスクの計算によって証明ができることが予想される.しかしこの不等式の導出は困難と考えられてきた.Hをp×pの直交行列のなす群 上の不変測度に従いT,T-1SeT-1と独立な確率変数行列とする.そのとき(2)に対応して 上の不変測度に従いT,T-1SeT-1と独立な確率変数行列とする.そのとき(2)に対応して   が成立することをここでは証明した.この不等式はzonal多項式に関するいくつかの公式を用いることで示される.これを用いれば,H’P∧P’H=H’T-1SeT-1Hを与えたときの条件つきリスクを考えることで,制約付最尤推定量の不偏推定量に対する改良を示すことができる. 2.縮小推定量の平均二乗誤差の推定. p次元多変量正規分布に従う確率変数X,  における平均ベクトル を縮小推定量 を縮小推定量  を用いて推定したときの平均二乗誤差(以下MSE)  の推定問題について考える.このようなリスクの推定問題は用いた縮小推定量の確からしさを知る一つの指標として,あるいは縮小推定量を用いた信頼区間の構成に役に立つことが考えられ,実際過去にもいくつかの決定理論的立場の研究がある.しかしそれらはやや不十分である上,縮小推定量としては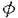 (W)=(p-2)/(n+2)のJames-Stein推定量の場合のみが扱われてきた.しかし,James-Stein推定量は非許容的であることが知られており,これを改良する推定量も多く知られていることもあるので,第六章では一般の (W)=(p-2)/(n+2)のJames-Stein推定量の場合のみが扱われてきた.しかし,James-Stein推定量は非許容的であることが知られており,これを改良する推定量も多く知られていることもあるので,第六章では一般の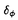 のMSEについて決定論的結果を与えることを目的とした. のMSEについて決定論的結果を与えることを目的とした. まず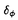 のMSE不偏推定量は, のMSE不偏推定量は,  で与えられることを示した.ここで,  である. しかしこの推定量は通常の縮小推定量の場合,負値を取り得るという弊害がある.二乗損失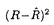 でこの推定を評価するとき,0でtruncateした推定量がUMVU推定量を優越するのは自明である.しかし,以下の推定量で二乗損失に関しこの0-truncateの推定量をも改良できることを示した.改良型推定量は でこの推定を評価するとき,0でtruncateした推定量がUMVU推定量を優越するのは自明である.しかし,以下の推定量で二乗損失に関しこの0-truncateの推定量をも改良できることを示した.改良型推定量は  で与えられる.この結果は分散共分散行列の際にも用いたWの条件つきの二乗損失の期待値を計算することで導出される.この推定量はpに比してnが小さい場合に有効な推定量であることがシミュレーションにより確かめられた.第七章では,この議論を線形の変量モデルにおける予測の問題に適用し,同等の結果を得ると同時に,シミュレーションによりここでのMSE推定量が小標本の場合に信頼区間の構成にも有効であり,通常のt分布の基づく信頼区間よりも優れたものが得られることが示唆された. |
| 審査要旨 | | 正規分布モデルを基礎とする統計的推測においては,多くの場合完備十分統計量が存在し自明に最小分散不偏推定量が求められる.しかしながら,1956年にSteinが確率変数Xi,i=1…K,が互いに独立に正規分布N(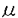 i, i,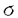 2)に従うという単純な設定の下で,K 2)に従うという単純な設定の下で,K 3の時に自明な最小分散不偏推定量 3の時に自明な最小分散不偏推定量 =Xiを総平均二乗誤差の意味で改良する推定量を構成して以来,種々の設定で最小分散不偏推定量を改良する試みがなされてきた.本論文はその流れの中で,多変量正規分布における =Xiを総平均二乗誤差の意味で改良する推定量を構成して以来,種々の設定で最小分散不偏推定量を改良する試みがなされてきた.本論文はその流れの中で,多変量正規分布における 1.分散共分散行列の推定, 2.平均ベクトルの縮小推定量の平均二乗誤差の推定, という二つの推定問題を取り上げ,それぞれに関し新たな改良推定量を理論的に導くとともに,その良さをシミュレーションにより確認したものであり,全2部8章より構成されている. 第1章は全4章からなる第1部の序章であり,多変量正規分布における分散共分散行列の推定問題を概観している.とくに1元配置母数模型を扱う第2章,第3章の設定が,互いに独立に多(p)変量正規分布N(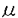 i, i, )に従うXi,i=1,…,K,およびそれらとは独立にウィシャート分布Wp(n, )に従うXi,i=1,…,K,およびそれらとは独立にウィシャート分布Wp(n, )に従う標本共分散行列Sとに基づく )に従う標本共分散行列Sとに基づく の推定問題であり,アフィン変換に関し不変な損失関数 の推定問題であり,アフィン変換に関し不変な損失関数 を想定することについて述べている.このとき,自明な共変最小分散不偏推定量 0=n-1Sが非許容的であり,それを改良する主として二つの接近法があることを紹介している.まず第一の接近法として,1変量(p=1)の場合にSteinがX1,…,XKの情報を利用した打ち切り推定量を提案し,Sinha & Ghoshがそれを直接的な方法で多変量に拡張し推定量 0=n-1Sが非許容的であり,それを改良する主として二つの接近法があることを紹介している.まず第一の接近法として,1変量(p=1)の場合にSteinがX1,…,XKの情報を利用した打ち切り推定量を提案し,Sinha & Ghoshがそれを直接的な方法で多変量に拡張し推定量 を提案した. を提案した. は は 0は改良するものの,その不連続性ゆえに十分な改良は得られない.そこで,とくにK=1の場合に,PerronおよびKubokawa他の連続推定量が提案されることになる.本論文の第2章はこの流れに沿った拡張を与える. 0は改良するものの,その不連続性ゆえに十分な改良は得られない.そこで,とくにK=1の場合に,PerronおよびKubokawa他の連続推定量が提案されることになる.本論文の第2章はこの流れに沿った拡張を与える. 0を改良する第二の接近法はミニマックス推定量であり,第3章で有望なミニマックス推定量が提案される.一方,第4章が1元配置変量模型の二つの分散行列成分の推定問題を扱うこと,ならびにこの設定における最小分散不偏推定量の非許容性とその改良推定量が提案されてきた経緯について述べている. 0を改良する第二の接近法はミニマックス推定量であり,第3章で有望なミニマックス推定量が提案される.一方,第4章が1元配置変量模型の二つの分散行列成分の推定問題を扱うこと,ならびにこの設定における最小分散不偏推定量の非許容性とその改良推定量が提案されてきた経緯について述べている. 第2章でまず提案される推定量は である.ただし,UはUU’=Sを満たす任意のp×p行列,H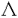 H’はU-1XX’U’-1のスペクトル分解, H’はU-1XX’U’-1のスペクトル分解,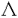 =diag( =diag( i)そしてHは直交行列である.Uの任意性に関わらず,UHは一意である.推定量 i)そしてHは直交行列である.Uの任意性に関わらず,UHは一意である.推定量 TRにおいて, TRにおいて,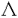 TR=diag{min(n-1K, TR=diag{min(n-1K, i)}がSinha & Ghoshの推定量 i)}がSinha & Ghoshの推定量 の不連続性を解消する本質的部分であり,K=1の特別な場合としてPerronの推定量を含んでいる. の不連続性を解消する本質的部分であり,K=1の特別な場合としてPerronの推定量を含んでいる. TRが損失関数L( TRが損失関数L( , , )の意味で )の意味で 0および 0および を真に改良することを示したのが本章の理論的成果である.次に を真に改良することを示したのが本章の理論的成果である.次に 0を改良する推定量として新たに 0を改良する推定量として新たに を提案し,それが を提案し,それが TRを改良するとの推測を述べているが,厳密な証明には至っていない.以上の考察を確認するためのシミュレーションを行い,新しく提案した推定量 TRを改良するとの推測を述べているが,厳密な証明には至っていない.以上の考察を確認するためのシミュレーションを行い,新しく提案した推定量 TRおよび TRおよび の両者,とくに後者が の両者,とくに後者が 0, 0, を改良する有望な推定量であることを示している. を改良する有望な推定量であることを示している. 第3章では,第二の接近法であるミニマックス推定量の改良を論じ,新たな推定量を提案している. 0を改良するミニマックス推定量としてまず,James & Steinの推定量 0を改良するミニマックス推定量としてまず,James & Steinの推定量 JSが提案され,さらにDey-Srinivasanにより改良推定量 JSが提案され,さらにDey-Srinivasanにより改良推定量 DS=UCU’が提案された.ただし,ここではSのスペクトル分解S=QLQ’より,U=QL1/2と定義し,C=diag{(n+p+1-2i)-1}である.本章では DS=UCU’が提案された.ただし,ここではSのスペクトル分解S=QLQ’より,U=QL1/2と定義し,C=diag{(n+p+1-2i)-1}である.本章では DSを改良する推定量のクラス DSを改良する推定量のクラス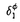 = =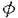 ( ( )UCU’を論じ, )UCU’を論じ,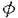 ( ( )の満たすべき十分条件を与えると共に,具体的な改良推定量を与えるものとして, )の満たすべき十分条件を与えると共に,具体的な改良推定量を与えるものとして, を導いている.対応する推定量は TR1と書かれる.次に推定量のクラスを TR1と書かれる.次に推定量のクラスを に拡げ, が が DSを改良するために DSを改良するために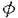 i( i( )の満たすべき十分条件を与えると共に,それを満たす具体的な関数を導いている.対応する推定量は )の満たすべき十分条件を与えると共に,それを満たす具体的な関数を導いている.対応する推定量は TR2と書かれる. TR2と書かれる. DSの改良としてはこの他にSheena & Takemuraによる二つの推定量があるが,本章では引き続きそれらの非許容性を示すと共に改良推定量として, DSの改良としてはこの他にSheena & Takemuraによる二つの推定量があるが,本章では引き続きそれらの非許容性を示すと共に改良推定量として, TR3, TR3, TR4を提案している.これらに第2章で提案した推定量を加えたシミュレーションによる検討では本章の方法,なかでも TR4を提案している.これらに第2章で提案した推定量を加えたシミュレーションによる検討では本章の方法,なかでも TR2の有位性が示されている. TR2の有位性が示されている. 第4章は多変量1元配置変量模型 における二つの分散行列成分の推定問題を扱う.ただし, i,∈ijはそれぞれ,また互いに独立とする.群内および群間の標本分散行列をそれぞれSeおよびSvとするとき, i,∈ijはそれぞれ,また互いに独立とする.群内および群間の標本分散行列をそれぞれSeおよびSvとするとき, e, e, vに対応する自明な最小分散不偏推定量 vに対応する自明な最小分散不偏推定量 は前2章で用いた損失関数に関し非許容的であり,とくに は正の確率で負値定符号行列となる本質的欠陥を有する.そこで,確率1で非負値を取る制約付最尤推定量 は正の確率で負値定符号行列となる本質的欠陥を有する.そこで,確率1で非負値を取る制約付最尤推定量 , , が提案されたが,その理論的性質は十分に解明されていなかった.そこで本章では,一連の確率行列に関する不等式を開発することにより, が提案されたが,その理論的性質は十分に解明されていなかった.そこで本章では,一連の確率行列に関する不等式を開発することにより, および および がそれぞれ がそれぞれ , , を改良することを理論的に証明した.次に3章と同様の方法により, を改良することを理論的に証明した.次に3章と同様の方法により, eおよび eおよび vに対する一連のミニマックス推定量を構成し,それらが従来提案されている推定量を改良することをシミュレーションにより確認している.さらにそれら改良ミニマックス推定量の合成により群間成分である vに対する一連のミニマックス推定量を構成し,それらが従来提案されている推定量を改良することをシミュレーションにより確認している.さらにそれら改良ミニマックス推定量の合成により群間成分である vを推定することを提案しているが,その推定量は非負とならない確率が常に十分小さいとは限らないという意味において今後に課題を残している. vを推定することを提案しているが,その推定量は非負とならない確率が常に十分小さいとは限らないという意味において今後に課題を残している. 第5章は全4章からなる第2部の序章であり,多変量正規分布の平均ベクトルの縮小推定量,および小領域問題に適用される混合線形モデルによる縮小予測推定量の精度評価の研究の経緯を紹介している. まず第6章で扱われる問題は,多(p)変量正規分布N( , ,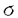 2Ip)に従う確率変数Xに基づく平均ベクトル 2Ip)に従う確率変数Xに基づく平均ベクトル の縮小推定量 の縮小推定量 の精度評価である.ただし統計量SはXとは独立に自由度nの 2変数の定数倍 2変数の定数倍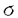 2 2 nに従うものとし, nに従うものとし,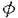 (W)は絶対連続かつ (W)は絶対連続かつ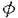 (W), (W),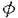 ’(W)共に有界とする.従来提案されている縮小推定量はすべてこのクラスに属している.かかる非線形な縮小推定量 ’(W)共に有界とする.従来提案されている縮小推定量はすべてこのクラスに属している.かかる非線形な縮小推定量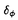 の平均二乗誤差を評価することはそれ自体容易なことではないが,本章ではその最小分散不偏推定量を求めたうえ,さらにそれを平均二乗誤差の意味で改良する縮小推定量を提案している.またシミュレーションにより,とくに非心度‖ の平均二乗誤差を評価することはそれ自体容易なことではないが,本章ではその最小分散不偏推定量を求めたうえ,さらにそれを平均二乗誤差の意味で改良する縮小推定量を提案している.またシミュレーションにより,とくに非心度‖ ‖/ ‖/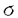 2の小さいとき,その不偏推定量を改良する程度が十分に大きいことを確認している. 2の小さいとき,その不偏推定量を改良する程度が十分に大きいことを確認している. 第7章で扱われるのは混合線形モデル における第i水準の効果xi + + iの予測量の評価である.これは小領域問題と呼ばれ,xiは小領域iの母数型説明変数, iの予測量の評価である.これは小領域問題と呼ばれ,xiは小領域iの母数型説明変数, iは同確率的変動成分,そして∈ijは誤差変量であり, iは同確率的変動成分,そして∈ijは誤差変量であり, i,∈ijはそれぞれ,また相互に独立である.これは領域全体の回帰成分に小領域の特徴を加味して i,∈ijはそれぞれ,また相互に独立である.これは領域全体の回帰成分に小領域の特徴を加味して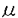 iの推定精度を上げようとするもので,農作物の収率の推定など広い応用分野を持つ.本章では縮小推定量 iの推定精度を上げようとするもので,農作物の収率の推定など広い応用分野を持つ.本章では縮小推定量 の平均二乗誤差の不偏推定量,ならびにその改良推定量を与えると共にそれを の平均二乗誤差の不偏推定量,ならびにその改良推定量を与えると共にそれを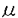 iの信頼区間構成に役立てることを提案している.かかる非線形な推定量に基づき,適切な信頼区間を構成することは応用上の貢献が大きい. iの信頼区間構成に役立てることを提案している.かかる非線形な推定量に基づき,適切な信頼区間を構成することは応用上の貢献が大きい. 第8章は以上の結果のまとめである. 以上を要するに,本論文は,(1)多変量正規分布の分散行列の推定,および(2)多変量正規分布の平均の縮小推定量の平均二乗誤差の推定という二つの問題に関し,従来提案されている推定量の非許容性を理論的に証明すると共に,実際にそれらを改良する推定量を構成し,その有用性を明らかにしたものであり,工学的意義が大きい. よって本論文は博士(工学)の学位請求論文として合格と認められる. |