| 内容要旨 | | 1.はじめに あるクラスの非線形放物型偏微分方程式においては,与えられた初期値から出発した解が時間無限大まで延長されないで,有限時間で特異性を生じることがしばしばある.このような現象を解の爆発(blow-up)といい,特異性が生じる時刻を爆発時刻(blow-up time)とよぶ.多くの場合,爆発時刻で爆発解の何らかのノルムが発散する. 様々な自然現象に対して,それを数学的に研究するための数理モデルが提案・導出され,そのモデルを記述する偏微分方程式(モデル方程式)の研究が盛んに進められている.燃焼問題のモデル方程式や,生物数学に現れるモデル方程式,また,曲率流方程式のような微分幾何学に現れる方程式など,様々な方程式の解に爆発現象が生じることが知られている.爆発現象の研究は数学的にも非常に興味深い問題であるが,それのみならず,上記のようなモデルを深く理解するためにも重要であることは明らかであろう. 藤田[5]による先駆的な仕事以来,解の爆発現象は様々な角度から研究されてきている.「いつ,どこで,どのように爆発するのか」という問題について,多くの仕事がなされ,今日では,いくつかの特定の方程式についてではあるが,爆発時刻の近くでの解の挙動についてかなり詳細な情報が得られるまでになっている.とはいえ,多くの未解決な問題が残されており,今なお盛んに研究が続けられている. 本論文では,爆発現象を有する方程式を何らかの方法で近似した場合,その近似方程式によって爆発現象がどこまで再現できるのか,という問題を考察する.このような問題を取り上げる理由の一つは,数値計算による爆発現象の観察の可能性を探ることにある.与えられた方程式の解を数値計算する際,元の問題を離散化した近似問題を考える必要があるが,一般的に,数値計算によって爆発現象を追跡するのは非常に困難である.これは,爆発とともに解のノルムが無限大に発散することに由来する困難である.本論文では,特に,爆発時刻に焦点をあて,解が爆発する時刻が近似問題の解析によってどこまで正確にとらえられるかを探ることにする. これまでに,爆発時刻を数値的に観察するための手法がいくつか考案されている.爆発時刻付近での爆発解の形状を観察することができる数値計算スキームとして,方程式のもつスケール変換不変性を利用したBerger & Kohn[2]の方法(リスケーリング・アルゴリズム)や,Buddら[3]によるMMPDEと呼ばれる方法が開発されている.爆発時刻の数値計算可能性についても早い時期から研究がおこなわれている.中川[6]は,ut=uxx+u2という方程式に対する,ある有限差分スキームの研究を行ない,そのスキームの解の収束性や,数値的な爆発時刻が元の問題の爆発時刻へ収束することを示している.Chen[4]はut=uxx+upに対するある有限差分スキームを考察し,そのスキームの解の挙動や,爆発時刻の収束性(1<p<3)を示している.また,最近Abia[1]らは,上記のような方程式を含むやや広いクラスの方程式に対して,空間方向のみを有限差分近似した半離散近似問題を考察し,その近似問題の爆発時刻の収束性を示している. 本論文では,近似問題の爆発時刻の,元の問題の爆発時刻への収束性をかなり一般的な枠組の中で論じ,その結果をいくつかの具体的な問題に対して応用した. 2.主結果 放物型の非線形偏微分方程式  の初期値境界値問題を考える.この問題は,ある関数空間Xの中で一意的な時間局所解u(・,t)∈Xを持つとする.さらに,ある有限な時刻T>0があって,その解はTを越えては,Xの中で延長できないものとする.すなわち, (A0)(1)の解u(・,t)は時刻Tで爆発する ものとする.さらに,ある汎関数J:X→ があって,(1)の爆発解uに対して, があって,(1)の爆発解uに対して,  あるいは,  のいずれかが成り立っているものとする.このような汎関数Jの例は,個々の爆発問題に対して数多く見出すことができる. 今方程式(1)が,以下のような,パラメータhを含む方程式の族によって近似されているとしよう:  ここで,hは近似を表すパラメータで,0に近づくとき近似の精度が良くなるものとする.また,▽hu, hu, hu, h,xhはそれぞれ▽u, h,xhはそれぞれ▽u, u, u, ,xの近似量を表す.例えば,(1)を空間方向にのみ有限差分近似して得られる常微分方程式系などが(1h)の例である.この場合にはパラメータhは空間メッシュのサイズに対応する.この近似問題(1h)に対して,上の汎関数Jを近似する汎関数Jh:Xh→ ,xの近似量を表す.例えば,(1)を空間方向にのみ有限差分近似して得られる常微分方程式系などが(1h)の例である.この場合にはパラメータhは空間メッシュのサイズに対応する.この近似問題(1h)に対して,上の汎関数Jを近似する汎関数Jh:Xh→ が定まっているとする. が定まっているとする. さて,この論文の主結果は「(1h)の解uhが(1)の解uに汎関数の意味で収束し(下記の仮定(A2)),汎関数J,Jhがある条件(下記の(A1),(A1)’,(A1)"のいずれか)を満たせば,近似解uhは有限時間Thで爆発し,その爆発時刻Thはuの爆発時刻Tに収束する」というものである. 以下,J,Jhの満たすべき条件について説明しよう.まず,以下の2つの微分不等式を考える.第一の不等式は次の形のものである:  ここで,関数Fは滑らかで,  を満たすものとする.第二の不等式は次の形のものである:  ここでcは非負の定数である. 以下のうちのいずれかの条件をJおよびJhに課すものとする. (A1)解u(・,t)∈Xに対して(a)または(b)がが成り立ち,ある連続関数Fと非負の定数cがあって各近似解uhに対してJh[uh](t)は(I1)および(I2)を満たす. (A1)’解u(・,t)∈Xに対して(a)が成り立ち,ある連続関数Fがあって各近似解uhに対してJh[uh](t)は(I1)を満たす. (A1)"解u(・,t)∈Xに対して(b)が成立し,ある非負の定数cがあって各近似解uhに対してJh[uh](t)は(I2)を満たす.さらに,定数M<∞があってJ[u](t) MかつJh[uh](t) MかつJh[uh](t) Mが成立する. Mが成立する. また,いずれの場合にも (A2)近似解uhは,解uを次の意味で近似している:任意の >0に対して, >0に対して, 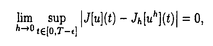 を課すものとする. 以上の仮定の下に,以下の3つの定理が得られる. 定理1仮定(A0),(A1),(A2)の下で,十分小さなhに対して近似解uhは時刻Thで爆発し が成立する. が成立する. 定理2仮定(A0),(A1)’,(A2)の下で,十分小さなhに対して近似解uhは時刻Thで爆発し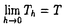 が成立する. が成立する. 定理3仮定(A0),(A1)",(A2)の下で,十分小さなhに対して近似解uhは時刻Thで爆発し が成立する. が成立する. 本論文の結果は数値計算への応用以外の側面があることに注意しておこう.上記の定理の系として,解の爆発時刻が初期値に連続的に依存することが得られる.解の爆発は,一見非常にとらえにくい不安定な現象のように見えるが,ある意味で安定な構造を持つことを本論文の結果は示唆しているのである. 3.応用例について 主結果の主張は,「元の問題に(A1)((A1)’,(A1)")を満たす汎関数Jが存在し,近似問題がこの汎関数を精度良く近似していれば,近似問題によって爆発時刻の近似が可能である」ということである.このような状況が多くの爆発問題に対して成立しているものと期待される. この論文では,以下に述べる3つの例に対して定理が適用可能であることを示した.以下の例では,いずれも,近似問題として空間方向を有限差分近似した半離散近似問題を採用した. 最初の例は,一般化された曲率流である.これは2次元平面内の閉凸曲線が法線方向に,曲率の冪乗に比例した速さで運動する問題である.この問題の解として有限時間内に特異性を生じるものが存在することは良く知られている.我々は定理2及び3を用いて,近似爆発時刻の収束性を示した. 次の例では,半線形方物型方程式ut= u+f(u)の解の爆発を扱った.ここに非線形項はf=up(p>1)もしくはeuとした.我々は,定理2及び1を用いて,近似爆発時刻の収束性を示した.この結果は,先に述べたAbiaらの結果を包含するものである. u+f(u)の解の爆発を扱った.ここに非線形項はf=up(p>1)もしくはeuとした.我々は,定理2及び1を用いて,近似爆発時刻の収束性を示した.この結果は,先に述べたAbiaらの結果を包含するものである. 最後の例は,Quenching問題である.これは正の解の一部分が有限時間で0になり,その際解の時間微分が無限大に発散する現象である.我々は定理3を用いて爆発時刻の収束性を示した. 参考文献[1]L.M.Abia,J.C.Lopez-Marcos,and J.Martinez.On the blow-up time convergence of semidiscretizations of reaction-diffusion equations.Appl.Numer.Math.,26:399-414,1998.[2]M.Berger and R.V.Kohn.A rescaling algorithm for the numerical calculation of blowing-up solutions.Comm.Pure Appl.Math.,41:841-863,1988.[3]C.J.Budd,W.Huang,and R.Russell.Moving mesh methods for problems with blow-up.SIAM J.Sci.Comput.,17:305-327,1996.[4]Y.G.Chen.Asymptotic behaviours of blowing-up solutions for finite difference analogue of ut=uxx+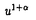 .J.Fac.Sci.Univ.Tokyo;Sec IA,Math.,33:541-574,1986.[5]H.Fujita.On the blowing up of solutions to the Cauchy problem ut= .J.Fac.Sci.Univ.Tokyo;Sec IA,Math.,33:541-574,1986.[5]H.Fujita.On the blowing up of solutions to the Cauchy problem ut= u+ u+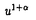 .J.Fac.Sci.Univ.of Tokyo,13:109-124,1966.[6]T.Nakagawa.Blowing up of a finite difference solution to ut=uxx+u2.Appl.Math.Optim.,2:337-350,1976. .J.Fac.Sci.Univ.of Tokyo,13:109-124,1966.[6]T.Nakagawa.Blowing up of a finite difference solution to ut=uxx+u2.Appl.Math.Optim.,2:337-350,1976. |
| 審査要旨 | | 論文提出者 牛島 健夫は,非線形熱方程式の解の爆発という現象が近似方程式によってどれだけ忠実に再現されるかという問題を,爆発時刻の側面に焦点をあてて一般的な枠組みで論じ,その成果を種々の具体的な方程式に応用した. あるクラスの非線形放物型偏微分方程式においては,与えられた初期値から出発した解が時間無限大まで延長されないで,有限時間で特異性を生じることがしばしばある.このような現象を解の爆発(blow-up)といい,特異性が生じる時刻を爆発時刻(blow-up time)とよぶ.多くの場合,爆発時刻で爆発解の何らかのノルムが発散する. 論文提出者は,爆発現象を有する方程式を何らかの方法で近似した場合,その近似方程式によって爆発現象がどこまで再現できるのか,という問題を考察した.このような問題を取り上げた理由の一つは,数値計算による爆発現象の観察の可能性を探ることにある.与えられた方程式の解を数値計算する際,元の問題を離散化した近似問題を考える必要があるが,一般的に,数値計算によって爆発現象を追跡するのは,非常に困難である.これは,爆発とともに解のノルムが無限大に発散することに由来する困難である.論文提出者は,特に,爆発時刻に焦点をあて,解が爆発する時刻が近似問題の解析によってどこまで正確にとらえられるかを探った. 爆発時刻を数値的に観察するための手法は,これまでにいくつか考案されている.爆発時刻付近での爆発解の形状を観察することができる数値計算スキームとして,方程式のもつスケール変換不変性を利用したBerger-Kohnの方法(リスケーリング・アルゴリズム)や,BuddらによるMMPDEと呼ばれる方法が開発されている.爆発時刻の数値計算可能性についても早い時期から研究がおこなわれている.中川は,ut=uxx+u2という方程式に対する,ある有限差分スキームの研究を行ない,そのスキームの解の収束性や,数値的な爆発時刻が元の問題の爆発時刻へ収束することを示している.Chenはut=uxx+upに対するある有限差分スキームを考察し,そのスキームの解の挙動や,爆発時刻の収束性(1<p<3)を示している.また,最近Abiaらは,上記のような方程式を含むやや広いクラスの方程式に対して,空間方向のみを有限差分近似した半離散近似問題を考察し,その近似問題の爆発時刻の収束性を示している. これに対し,論文提出者は,近似問題の解の爆発時刻が真の解の爆発時刻に収束するためには,方程式がどのような条件をみたしていればよいかをかなり一般的な枠組の中で論じた.具体的には,もとの方程式および近似方程式に対して,ある微分不等式をみたす1種類または2種類の汎関数が存在すれば,爆発時刻の収束性が導かれることが示されている. 爆発時刻の評価に,ある種の汎関数を用いるのは以前からなされていたが,いずれも1種類の汎関数しか用いていなかった.論文提出者は,性質の異なる2種類の汎関数を巧妙に用いており,これにより,理論が適用できる範囲が大幅に広がっている. 提出論文では,応用例として3つの問題が取り上げられている.最初の例は,一般化された曲率流である.これは,2次元平面内の閉凸曲線が法線方向に,曲率の冪乗に比例した速さで運動する問題である.2番目の例は,ut= u+f(u)という形の半線形熱方程式である.最後の例は,Quenching問題である.これは正の解の一部分が有限時間で0になり,その際解の時間微分が無限大に発散する現象である. u+f(u)という形の半線形熱方程式である.最後の例は,Quenching問題である.これは正の解の一部分が有限時間で0になり,その際解の時間微分が無限大に発散する現象である. なお,論文提出者の得た結果は,数値計算への応用にとどまらない.例えば,解の爆発時刻が初期値や方程式内のパラメータに連続的に依存することも,主定理の系として得られる.解の爆発は,一見非常にとらえにくい不安定な現象のように見えるが,ある意味で安定な構造を持つことをこの結果は示唆しているのである. 論文提出者の仕事は,これまで散発的にしか研究がなされていなかった爆発現象の数値シミュレーションの正当性を,比較的一般的な枠組みで論じた初めての試みであり,また,爆発現象のある意味での構造安定性を示唆している点でも意義深い. 以上の諸点を考慮した結果,論文提出者牛島健夫は,博士(数理科学)の学位を受けるにふさわしい十分な資格があると認める. |