この論文では、Rn(n 3)で外力f(x)をもつ次のような半線型熱方程式の初期値問題を考える: 3)で外力f(x)をもつ次のような半線型熱方程式の初期値問題を考える:   ここで、 である。 である。 この方程式に対応する定常問題は次のとおりである:  外力がない場合(f(x)≡0)の方程式(0.1)については、Fujita[5]が、 かつ かつ が十分小さいという条件のもとで、この初期値問題が時間大域的な強解をもつことを最初に証明した。また、彼は同時に が十分小さいという条件のもとで、この初期値問題が時間大域的な強解をもつことを最初に証明した。また、彼は同時に という条件が、非負の自明でない初期値に対する時間大域的な強解の存在に必要であることも証明した(Haraux and Weissler[9],Hayakawa[10],Kobayashi,Sirao and Tanaka[13]参照)。また、Weissler[24]は という条件が、非負の自明でない初期値に対する時間大域的な強解の存在に必要であることも証明した(Haraux and Weissler[9],Hayakawa[10],Kobayashi,Sirao and Tanaka[13]参照)。また、Weissler[24]は (p=n( (p=n( -1)/2>1)が十分小さいとき、解の大域的な存在を証明した。 -1)/2>1)が十分小さいとき、解の大域的な存在を証明した。 一方、初期値を測度とする初期値問題の研究もある。BrezisとFriedman[4]は初期値 (x)に対する時間局所的な解の存在には、 (x)に対する時間局所的な解の存在には、 という条件が必要かつ十分であることを証明した。BarasとPierre[1]は、初期値がRadon測度の場合のさまざまな研究をした。Niwa[18]は、初期値を与える測度空間がMorrey型であるような初期値問題について、局所的なwell-posednessや大域的なwell-posednessの十分条件を得た。KozonoとYamazaki[15]は、Besov型のMorrey空間で初期値に対する時間局所的及び時間大域的な解を得た。この解は外力f(x)≡0の場合の方程式(0.1)-(0.2)の定常解0に対する安定性と考えることができる。彼ら[16]はまた、外力に対する適当な仮定のもとでNavier-Stokes方程式に対するMorrey空間での小さな定常解の安定性を証明した。初期値を測度とするNavier-Stokes方程式の他の研究については、Giga[7,8],Kato[11,12],Kozono and Ymazaki[14,17],Taylor[22]などがある。以上のような研究に基づいて我々は、KozonoとYamazaki[15]の問題を一般化して初期値問題(0.1)-(0.2)に対し0でない定常解の安定性を考察した。 という条件が必要かつ十分であることを証明した。BarasとPierre[1]は、初期値がRadon測度の場合のさまざまな研究をした。Niwa[18]は、初期値を与える測度空間がMorrey型であるような初期値問題について、局所的なwell-posednessや大域的なwell-posednessの十分条件を得た。KozonoとYamazaki[15]は、Besov型のMorrey空間で初期値に対する時間局所的及び時間大域的な解を得た。この解は外力f(x)≡0の場合の方程式(0.1)-(0.2)の定常解0に対する安定性と考えることができる。彼ら[16]はまた、外力に対する適当な仮定のもとでNavier-Stokes方程式に対するMorrey空間での小さな定常解の安定性を証明した。初期値を測度とするNavier-Stokes方程式の他の研究については、Giga[7,8],Kato[11,12],Kozono and Ymazaki[14,17],Taylor[22]などがある。以上のような研究に基づいて我々は、KozonoとYamazaki[15]の問題を一般化して初期値問題(0.1)-(0.2)に対し0でない定常解の安定性を考察した。 この論文の方針としては、まずBanach逆写像定理を用いて、Morrey空間の元f(x)に対し適当な仮定のもとで(0.3)に対応する定常問題の小さな解の一意存在を証明する。次に、半群の方法を用いて、初期値a(x)が定常解に十分近いとき、初期値問題(0.1)-(0.2)の時間大域的な一意可解性を証明する。そのあと、いろいろなMorrey空間での小さな定常解の安定性を調べた。。 結果は大きく二つの部分に分かれる。 1.The Stability of Small Stationary Solutions in Morrey Spaces of the Semilinear Heat Equations. 2.Semilinear Heat Equations with distributions in Morrey Spaces as initial data. まず、第一部では、  3, 3, ∈Zであるような初期値問題を考える。即ち、次のような半線型熱方程式の初期値問題を考える: ∈Zであるような初期値問題を考える。即ち、次のような半線型熱方程式の初期値問題を考える: 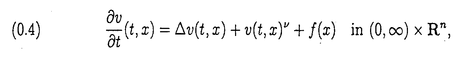  この方程式に対応する定常問題は次のとおりである:  主な結果は次の定理である。 Theorem 1.  3, 3, ∈Z, ∈Z,  q0 q0 p0=n( p0=n( -1)/2を仮定する。 -1)/2を仮定する。 このとき、正数 0と 0と (0)=0をみたす[0, (0)=0をみたす[0, 0]上の連続な狭義単調増加関数 0]上の連続な狭義単調増加関数 ( ( )が存在し、次を満たす。 )が存在し、次を満たす。 (1)任意のf(x)∈D’に対し、 の中で(0.6)の解 の中で(0.6)の解 (x)は高々1つしかない。 (x)は高々1つしかない。 (2) を満たす任意の を満たす任意の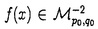 に対して、(0.6)の解 に対して、(0.6)の解 が存在し、 が存在し、   ( ( )を満たす。 )を満たす。 Theorem 2. ,p0,q0はTheorem1と同じとし、p0<p< ,p0,q0はTheorem1と同じとし、p0<p< p0/2,q0<q p0/2,q0<q pq0/p0, pq0/p0, < <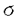 0< 0< とする。このとき、正数 とする。このとき、正数 1( 1(  0), 0), 0とM0を選んで、次を満たすようにできる。 0とM0を選んで、次を満たすようにできる。  を満たす任意の を満たす任意の とTheorem1(2)で得られた(2)の解 とTheorem1(2)で得られた(2)の解 (x)及び (x)及び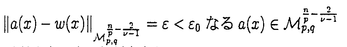 に対して、(0.4)-(0.5)の時間大域的な解 に対して、(0.4)-(0.5)の時間大域的な解 (t,x)が存在し、 (t,x)が存在し、   さらに、初期条件(0.5)は次の意味で成立する: 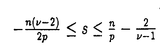 を満たす任意のsと任意のT’>0に対して、 を満たす任意のsと任意のT’>0に対して、  Theorem 3.Theorem2と同じ仮定とする。 任意の0<T ∞に対して、T’∈(0,T)に対する(0.7)、(0.8)と ∞に対して、T’∈(0,T)に対する(0.7)、(0.8)と (t,・)- (t,・)-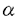 →0in →0in を満たす(0,T)×Rn上の(0.4)-(0.5)のいかなる解も、Theorem2の大域的な解の(0,T)×Rn上の制限でなければならない。 を満たす(0,T)×Rn上の(0.4)-(0.5)のいかなる解も、Theorem2の大域的な解の(0,T)×Rn上の制限でなければならない。 Remark 1.この結果は、Theorem2の時間大域的な解の一意性を示す。 Theorem 4.Theorem2と同じ仮定とする。  を満たす任意の を満たす任意の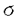 に対して、 に対して、 を満たす[0, を満たす[0, 0]上の連続な狭義単調増加関数 0]上の連続な狭義単調増加関数 が存在して、次を満たす。 が存在して、次を満たす。  Remark 2.p0,q0,p,qがTheorem2と同じならば、Lemma2.4とLemma2.1は包含関係 を意味する。よって、Theorem4で を意味する。よって、Theorem4で とし、 とし、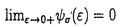 という結果を用いれば、評価(0.10)は、 という結果を用いれば、評価(0.10)は、 の位相で、定常解のLyapunov安定性を意味する。(0.10)の他の評価は、さまざまな位相 の位相で、定常解のLyapunov安定性を意味する。(0.10)の他の評価は、さまざまな位相 での漸近安定性を示す。 での漸近安定性を示す。 次に、第二部では、第一部の結果を次の2つの場合に分けてより一般的な条件 へ拡張する。 へ拡張する。   定理の主張は第一部と同様である。第一部と第二部では、証明に使われる評価が異なるので、それぞれの初期値問題に対する仮定が多少違うことに注意する。 |