| 内容要旨 | | 1. 複素数体C上定義された非特異代数多様体Xの部分多様体の有限和 niZi(ni∈Z,Zi⊂X閉部分多様体)を代数的サイクルという.代数的サイクルを有理同値とよばれる同値関係で割ったもののなす群をXのChow群といいCHr(X)(=CHdimX-r(X))とかく.ここでr∈Z>0はサイクルの余次元を表している.代数的サイクルとはこのように定義は非常に簡単なのであるが,Chow群についてこれを実際に計算することは極めて困難である. niZi(ni∈Z,Zi⊂X閉部分多様体)を代数的サイクルという.代数的サイクルを有理同値とよばれる同値関係で割ったもののなす群をXのChow群といいCHr(X)(=CHdimX-r(X))とかく.ここでr∈Z>0はサイクルの余次元を表している.代数的サイクルとはこのように定義は非常に簡単なのであるが,Chow群についてこれを実際に計算することは極めて困難である. 代数曲線のChow群の計算は19世紀,Abelによって成し遂げられた.有名なAbelの定理である.この定理により代数曲線上の次数0の0-cycleのなすChow群はその曲線のJacobi多様体と同型になる.この定理は余次元1,すなわち因子類群に対してはそのまま一般化される.すなわち非特異射影多様体の因子類群はその多様体のPicard多様体と同型になる. Abelの定理はChow群にAbel多様体の構造を持つことを主張した点において際立った定理である.代数的サイクルの定義をみる限りそのようなことは見受けられない.この美しい定理を任意余次元のChow群に対して一般化しようというのは自然な試みであった.0-cycleに対してはAlbanese写像CH0(X)deg=0→Alb(X)があり,また一般の代数的サイクルに対してはGriffiths-WeilのAbel-Jacobi写像CHr(X)hom→Jr(X)が定義されるから,これらが同型になることを示せばよいことになる.ところが,この試みはD.Mumfordによって否定的に終止符を打たれた.彼によれば幾何種数が0でない代数曲面に対してはAlbanese写像は単射にならないばかりかAbel多様体のような幾何的構造はどうやっても入らないほどCH0(X)は巨大になってしまうのである. Mumfordの定理により,一般に余次元が2以上の代数的サイクルのなすChow群は全く得体の知れない群であるとみなされるようになったばかりか,数学的研究価値さえ疑問視されるようになったのである. 2. このような情勢にあって,ただ一人,天才的洞察をもって代数的サイクルの研究に突破口を開いたのがS.Blochである.彼はAlbanese写像の核T(X)がH2(Xan,Z)/NS(X) Qでコントロールされることを看破し,有名なBloch予想を打ち立てた.これは,丁度Mumfordの定理の逆を主張するもので,幾何種数が0である代数曲面のAlbanese写像は単射になるだろうというものである.Bloch予想は小平次元が2でない曲面に対しては正しいことが分かっているが一般型曲面に対しては現在でも未解決である. Qでコントロールされることを看破し,有名なBloch予想を打ち立てた.これは,丁度Mumfordの定理の逆を主張するもので,幾何種数が0である代数曲面のAlbanese写像は単射になるだろうというものである.Bloch予想は小平次元が2でない曲面に対しては正しいことが分かっているが一般型曲面に対しては現在でも未解決である. このBlochの研究はDeligne,Beilinsonらの研究とともに混合モチーフの哲学へと発展していった.混合モチーフの哲学とは簡単にいえば,あらゆるcohomology理論を内包する"motivic cohomology"なるものの存在を主張する哲学である.すべての(複素)代数多様体のmotivic cohomology群の住みかを混合モチーフの圏といいM(C)とかく.混合モチーフと代数的サイクルとは次の美しい公式(Bloch-Beilinson公式)で結ばれている: 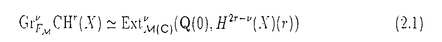 ここで左辺に現れているFMはChow群のmotivic filtrationであり,右辺のH(X)はmotivic cohomologyである."公式"と呼んでいるが勿論証明されたものではなく,むしろこのような公式を成立せしめるような理論を目指して研究されているといえる. 混合モチーフにせよmotivic filtrationにせよ定義されているわけではないのであるが,代数的サイクルの研究者にとって作業仮説としてだけでも重要な役割を果たしている.更にこれが現実の理論となればBloch予想を含む数多くの代数的サイクルに関する未解決問題が解決されることになる.従って混合モチーフの理論を完成させることはすべての代数的サイクルの研究者にとっての夢であるといっても過言ではない. Motivic filtrationを構成しようという試みはMurreや斎藤秀司らによって行われている.では,混合モチーフの圏M(C)はどのようにして構成したらよいであろうか?まず第一に思いつくのがDeligneの混合Hodge構造である.しかし,M(C)を混合Hodge構造の圏とした場合,Bloch-Beilinson公式(2.1)は成り立たない.実際,Carlsonの定理によれば混合Hodge構造の圏において2次以上のExtension群が消えてしまうのである. 3. 複素幾何(あるいは標数0の代数幾何)において強力な理論として多くの応用をもつHodge理論であるが,2次以上のExtension群が消えるという事実は致命的であった.われわれの興味の対象は にあるのであり,それを捉えるものが消えてしまっていては何の役にも立たないからである.実際このことが原因で,最近まで にあるのであり,それを捉えるものが消えてしまっていては何の役にも立たないからである.実際このことが原因で,最近まで に含まれるサイクルの研究はほとんど行われていなかった. に含まれるサイクルの研究はほとんど行われていなかった. ところが,ここ数年新しい動きが起こり始めた.Normal functionの理論である.Normal functionとはAbel-Jacobi写像を相対化したものであり,もともとP.GriffithsがHodge構造の変動について研究したとき,その応用として考えたものであるが,特に近年M.GreenおよびC.Voisinによるnormal functionの無限小不変量(infinitesimal invariants)の研究が代数的サイクルの研究において数々の著しい成果をあげていた.これらの研究に触発され,斎藤秀司氏はChow群のfiltrationを研究する上での画期的方法を見出した.斎藤氏は非特異射影多様体の族f:X→Sに対して,相対化filtration を定義し,更にDeligne cohomology上のLeray filtrationがサイクル写像 を定義し,更にDeligne cohomology上のLeray filtrationがサイクル写像 について両立すること,そして驚くべきことに,このサイクル写像は について両立すること,そして驚くべきことに,このサイクル写像は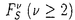 に含まれるサイクルの像が一般に消えないことを発見したのである.すなわち相対化することによって に含まれるサイクルの像が一般に消えないことを発見したのである.すなわち相対化することによって に含まれるサイクルが捉えられるようになるわけである. に含まれるサイクルが捉えられるようになるわけである. をhigher normal functionという.参考論文では更に,筆者と共同でhigher normal functionを使って,係数が十分一般な完全交叉多様体の0-cycleについてFN=0(N≫0)を支持する強い結果を証明している. をhigher normal functionという.参考論文では更に,筆者と共同でhigher normal functionを使って,係数が十分一般な完全交叉多様体の0-cycleについてFN=0(N≫0)を支持する強い結果を証明している. 4. 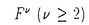 に含まれるサイクルを捉えるHodge理論的対象が発見されたのであるが,それは多様体の非特異射影的な族に対してのみ定義されるものであった.しかし理論的にもまた応用上においても,族に限らず通常の射影多様体に対してもそのような対象を定義することが望まれるところである. に含まれるサイクルを捉えるHodge理論的対象が発見されたのであるが,それは多様体の非特異射影的な族に対してのみ定義されるものであった.しかし理論的にもまた応用上においても,族に限らず通常の射影多様体に対してもそのような対象を定義することが望まれるところである. 本論文では斎藤氏のhigher normal functionに着想を得て,非特異射影多様体に対しても に含まれるサイクルを捉えるHodge理論的対象,数論的Hodge構造(arithmetic Hodge structure)を定義した.これは簡単にいえば混合Hodge構造に微分環Der(C/Q)の作用を付けたようなものである.そのアイデアを簡単に述べると次のようになる.Higher normal functionの成功の鍵は多様体の族を考えたことであった.従ってC上定義された代数多様体Xに対しても,Xを定義する方程式の係数をパラメーターとする族XS→S(Sは に含まれるサイクルを捉えるHodge理論的対象,数論的Hodge構造(arithmetic Hodge structure)を定義した.これは簡単にいえば混合Hodge構造に微分環Der(C/Q)の作用を付けたようなものである.そのアイデアを簡単に述べると次のようになる.Higher normal functionの成功の鍵は多様体の族を考えたことであった.従ってC上定義された代数多様体Xに対しても,Xを定義する方程式の係数をパラメーターとする族XS→S(Sは 上有限型なscheme)を考えればよい.Xは代数多様体であるから定義方程式も有限個でありまたその係数も有限個であるからこのようなモデルは常にとることができる.ただしこのようなモデルは一意的には定まらない.そこで数論的Hodge構造の圏 上有限型なscheme)を考えればよい.Xは代数多様体であるから定義方程式も有限個でありまたその係数も有限個であるからこのようなモデルは常にとることができる.ただしこのようなモデルは一意的には定まらない.そこで数論的Hodge構造の圏 (C)を,S上の混合Hodge構造の変動の圏の帰納的極限として定義する: (C)を,S上の混合Hodge構造の変動の圏の帰納的極限として定義する: .ここでSは .ここでSは 上のschemeなのでHodge構造の変動の定義のうち局所自由層とその上のHodge filtrationおよびGauss-Manin接続に関しては 上のschemeなのでHodge構造の変動の定義のうち局所自由層とその上のHodge filtrationおよびGauss-Manin接続に関しては 上定義されたものとして定義しておく方が自然である.こうして複素代数多様体に対してwell-definedに数論的Hodge構造の圏へcohomology関手が定義できる.更に代数的サイクルへの応用のためにはChow群から数論的Hodge構造の圏におけるExtension群へのサイクル写像を定義しておく必要がある.そのためには数論的Hodge構造のほかに更に数論的Hodge加群(arithmetic Hodge module)を定義しておけばよい. 上定義されたものとして定義しておく方が自然である.こうして複素代数多様体に対してwell-definedに数論的Hodge構造の圏へcohomology関手が定義できる.更に代数的サイクルへの応用のためにはChow群から数論的Hodge構造の圏におけるExtension群へのサイクル写像を定義しておく必要がある.そのためには数論的Hodge構造のほかに更に数論的Hodge加群(arithmetic Hodge module)を定義しておけばよい. 基本性質を述べよう. 1. (C)はAbel圏である. (C)はAbel圏である. 2.数論的Hodge構造のなす圏 (C)から混合Hodge構造のなす圏への忠実かつ完全な関手(realization functor)が存在する. (C)から混合Hodge構造のなす圏への忠実かつ完全な関手(realization functor)が存在する. 3.複素準射影的代数多様体のなす圏から数論的Hodge構造のなす圏 (C)へのcohomology関手Hが定義され,realization functorと合成すれば通常のBetti cohomology関手になる. (C)へのcohomology関手Hが定義され,realization functorと合成すれば通常のBetti cohomology関手になる. 4.非特異射影代数多様体Xに対してChow群上にfiltration Fが定義され,サイクル写像  が定義される.しかもこのサイクル写像の像は一般に0でない.特に数論的Hodge構造の圏において2次以上のExtension群は一般に消えない. M.GreenとP.Griffithsらも共同で数論的Hodge構造を筆者とは独立に定義している."Arithmetic Hodge structure"の命名は彼らによるもので,以来筆者も使用するようになった.ただし我々のものとは若干定義が異なる.もっとも異なる点は我々の数論的Hodge構造の定義にはQ-structureがデータとして含まれているが彼らの定義にはそれがない点である.すなわち,Hodge filtration付きDer(C/Q)加群としてのみ定義されている.従ってそれらのなす圏はAbel圏にはならず完全圏でしかない.しかしExtension群を考えることは可能で上記4にあるようなサイクル写像も定義され,やはりその像は一般に0にならないことが知られている. 本論文では数論的Hodge構造の応用として次の2つを行った.まず最初のものは,n点付き代数曲線のトレリ問題に関するものである.数論的Hodge構造は複素代数多様体に限らず,Cの部分体K上定義されたものに対しても同様なものが定義できる.その圏を Kとすると,自然な関手 Kとすると,自然な関手 K→ K→ (C)は忠実だが充満ではないのでそのことを利用して混合Hodge構造では区別不可能なK上の代数多様体の同型類を (C)は忠実だが充満ではないのでそのことを利用して混合Hodge構造では区別不可能なK上の代数多様体の同型類を Kの対象で区別しようという試みである.( Kの対象で区別しようという試みである.( (C)から混合Hodge構造の圏への関手が忠実であるが充満かどうかはよく分かっていない.)ある体K上定義された完備でない代数曲線のある族に対しその同型類が (C)から混合Hodge構造の圏への関手が忠実であるが充満かどうかはよく分かっていない.)ある体K上定義された完備でない代数曲線のある族に対しその同型類が Kの対象で区別できることを示したが,それらが混合Hodge構造によって区別できるかどうかはよく分かっておらずこの点は未完成な結果となっている.2つ目のものは数論的Hodge構造のモチベーションでもある代数的サイクルに関してである.次の予想を立てた:"代数曲面Xに対しAlbanese写像の核T(X)から Kの対象で区別できることを示したが,それらが混合Hodge構造によって区別できるかどうかはよく分かっておらずこの点は未完成な結果となっている.2つ目のものは数論的Hodge構造のモチベーションでもある代数的サイクルに関してである.次の予想を立てた:"代数曲面Xに対しAlbanese写像の核T(X)から (Q(0),H2(X)(2))への写像は単射になるだろう".この予想からBloch予想が従うことや,更に代数体上定義された代数曲面の0-cycleのなすChow群の階数の有限性が従うことも示した.なおこの予想に関してはM.Greenらの数論的Hodge構造では成り立たないことが知られている(C.Voisinの反例). (Q(0),H2(X)(2))への写像は単射になるだろう".この予想からBloch予想が従うことや,更に代数体上定義された代数曲面の0-cycleのなすChow群の階数の有限性が従うことも示した.なおこの予想に関してはM.Greenらの数論的Hodge構造では成り立たないことが知られている(C.Voisinの反例). 代数的サイクルへの応用についてはなお多くの課題が残されている.まず数論的Hodge構造のExtension群からnormal functionの無限小不変量を対応させる写像が定義される.従来のnormal functionの理論ではこの無限小不変量のみが計算可能で多くの結果はその解析によって得られた結果であったが,すべてのサイクルを捉えるわけではなかった.すなわち無限小不変量が消えてしまう0でないサイクルが存在した(上記C.Voisinの反例).しかし筆者のExtension群はすべて捉えるだろうと予想している.実際,無限小不変量は消えるが数論的Hodge構造の圏におけるExtension群上では消えないサイクルの例も構成できている.また代数体上定義された多様体のChow群の場合 と予想されている(Beilinson予想)が,それとの関係についても課題が残っている.これらについて詳しくは別に論文を準備中である. と予想されている(Beilinson予想)が,それとの関係についても課題が残っている.これらについて詳しくは別に論文を準備中である. 最後にこの文章を終えるにあたり斎藤秀司先生には特別な感謝の意を捧げたいと思う.筆者は修士課程在学中に先生と共同研究するという幸運に恵まれ,そのときhigher normal functionのアイデアを先生から教えていただいた. に含まれるサイクルの像が消えないことは筆者にとって真に驚くべきことであった.Higher normal functionなしにこのような論文は書けなかったことを明記しておく. に含まれるサイクルの像が消えないことは筆者にとって真に驚くべきことであった.Higher normal functionなしにこのような論文は書けなかったことを明記しておく. 加えて,筆者は博士課程在学中,2年間,大阪大学大学院臼井三平教授の下で委託指導を受けた.その間臼井先生からは数学上の指導,助言は言うに及ばず,たえず筆者を励まし続けるとともに筆者にとって心の支えにもなってくださった.筆者は先生に対する感謝の気持ちを生涯忘れることはないだろう. |
| 審査要旨 | | 朝倉君は本論文において,高次元における代数的サイクルの研究への応用を目標として,数論的Hodge構造の圏を定義し,その基礎理論を作るとともに,いくつかの応用を与えている. 歴史的には,代数的サイクルの研究は,代数曲線の因子に関するAbel-Jacobiの定理に始まる。現代風にいえば,これは複素数体 上の代数曲線の因子の有理同値類は,Hodge構造によって完全に統制されると言い表すことができる.一般次元においても,因子すなわち余次元1の代数的サイクルは,このようにHodge構造によって統制されている. 上の代数曲線の因子の有理同値類は,Hodge構造によって完全に統制されると言い表すことができる.一般次元においても,因子すなわち余次元1の代数的サイクルは,このようにHodge構造によって統制されている. しかし余次元2以上の場合は,はじめにMumfordによって代数曲面の0-サイクルに対して示されたように,因子の場合とは本質的に異なる現象が現れてくる.そして,この現象はその後のBloch,Deligne,Beilinsonらの研究により,混合モチーフの考えによって理解されるべきだと広く信じられるようになった. 朝倉君の研究は,この混合モチーフのなす圏のよい近似として,数論的Hodge構造の圏を定義し,そしてそれが代数的サイクルの研究に役立つものであることを示そうというものである.最近Voevodskyらによって,混合モチーフの圏のより幾何的な定義が与えられたが,朝倉君のはよりHodge理論的なものである.混合Hodge構造の圏自身も混合モチーフの圏の一次近似と考えることができる.これは因子については,十分役に立つものであるが,2次以上の高次のExt群が消えてしまうことなどから,高次元での代数的サイクルの研究には不十分なものである.またGreen-Griffithsは朝倉君と同様の考えに基づき数論的Hodge構造の異なる定義を与えたが,彼らのはAbel圏を成さず,その点で朝倉君の定義の方が優れている. 定義のアイデアは,複素数体を有理数体上定義された無限次元多様体の関数体と考え,この多様体上の混合Hodge構造の極限として複素数体上の混合モチーフをとらえようというものである.有理数体上の通常の有限次元の多様体について,その上の混合Hodge構造のvariationを考えることによって,モチーフをとらえようという考えは以前からあったが,複素数体をその極限ととらえ,組織的に考察しようというのは,新しい視点であり,代数的サイクルの研究に新しい道を開くことが期待される. 定義を簡単に述べる.まずXを の部分体k上定義されたsmoothなschemeとする.するとXにともなう複素多様体Xan上の混合Hodge構造Vと,X上の平坦接続とその重さFiltration,Hodge FiltrationでVのX上の下部構造を与えているものの組は自然にAbel圏をなす.これをMX/kと書く.次にKをkの(有限生成とは限らない)拡大体とする.体Kはk上smoothな環の極限と表わすことができる.そこでk上smoothなschemeに対し,上に定義した圏 の部分体k上定義されたsmoothなschemeとする.するとXにともなう複素多様体Xan上の混合Hodge構造Vと,X上の平坦接続とその重さFiltration,Hodge FiltrationでVのX上の下部構造を与えているものの組は自然にAbel圏をなす.これをMX/kと書く.次にKをkの(有限生成とは限らない)拡大体とする.体Kはk上smoothな環の極限と表わすことができる.そこでk上smoothなschemeに対し,上に定義した圏 の順極限としてK上の数論的Hodge構造の圏を定義する.これは自然にAbel圏をなし,cohomology関手(K上の多様体)→MKが定義される.またkの の順極限としてK上の数論的Hodge構造の圏を定義する.これは自然にAbel圏をなし,cohomology関手(K上の多様体)→MKが定義される.またkの への埋め込みのKへの延長K→ への埋め込みのKへの延長K→ を定めると,ファイバー関手MK/k→(混合Hodge構造)が定まる.ここで特にk= を定めると,ファイバー関手MK/k→(混合Hodge構造)が定まる.ここで特にk= ,K= ,K= とおいたもの とおいたもの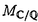 が が 上の数論的Hodge構造の圏である. 上の数論的Hodge構造の圏である. 本論文の中で次に述べる開曲線についてのTorelli型定理がこの定義の応用として与えられている.上と同様にkを の部分体とし,Cをk上のproper smoothな種数gの代数曲線とする.kの拡大体Kに対し,写像 の部分体とし,Cをk上のproper smoothな種数gの代数曲線とする.kの拡大体Kに対し,写像 が定義される.このとき次がなりたつ. 定理.n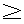 2g+1とし,Kをk上n-g変数の有理関数体とする.上の写像の,次の条件を満たす次数nのeffective因子Dからなる部分集合への制限は単射である.(条件)可逆層はk上定義され,k上のn-g次元射影空間 2g+1とし,Kをk上n-g変数の有理関数体とする.上の写像の,次の条件を満たす次数nのeffective因子Dからなる部分集合への制限は単射である.(条件)可逆層はk上定義され,k上のn-g次元射影空間 の Dが定めるK値点Spec K→ の Dが定めるK値点Spec K→ はその生成点への同型である. はその生成点への同型である. 証明はDの関数体のK上のGalois閉包のGalois群がn次対称群であることを使って,代数曲線上の2点は,その点が定める混合Hodge構造で決まることに帰着させてなされる.この定理が示すように,本論文で定義された数論的Hodge構造は代数的サイクルの研究に有効である. またBeilinson-Deligneによる,代数体上の高次Ext群が消えるという予想から,代数曲面に関するBloch予想を導くという観察も本文中で与えられている. 以上のようにこの論文で示された結果は代数的サイクルの研究という,現代の数論幾何学の重要な問題に新しい視点による考察を与えるものであり,国際的にも高い評価を受けている.よって論文提出者朝倉政典は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. |