| 内容要旨 | | 本論文に於いて著者はD-加群と導来圏の理論を用いて、線形偏微分方程式系の解の可解性と解の延長に関する研究を行った。結果は以下の通り大きく3部に分かれる。 (Part1)可解性について まず共著者の竹内潔氏と共に、ある種の多重特性の線形偏微分作用素Pに対して超関数(及びマイクロ関数)での可解性をD-加群や層のマイクロ台の理論を用いて研究した。扱う作用素Pが単純特性的(即ち作用素Pの主シンボル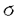 (P)の定める特性多様体Ch(D/DP)={ (P)の定める特性多様体Ch(D/DP)={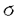 (P)=0}がsmooth)である場合には、Nirenberg-Treves・佐藤-柏原-河合ら(S-K-K)が、生成的な点に於いて可解性に関する必十条件を与えている。他方、より一般の多重特性的(即ち作用素Pの特性多様体が0-sectionの外で特異点又は重複点を持つ)な作用素の可解性の研究は一般に困難とされているが、佐藤超関数の枠組みではいくつかの場合にその困難が乗り越えられている。同枠組みに於いては超関数の性質を局所的に調べる場合、その特異性に着目し、解析関数をmoduloして考察する。その結果得られる「関数」をマイクロ関数といい、作用素Pの超関数としての可解性は、よく知られた解析関数での可解性(Cauchy-Kowalevskyの定理)とマイクロ関数での可解性に分解して判定する。特に作用素Pが双曲型、もしくは部分楕円型の場合はBony-Schapiraによってマイクロ関数、更には超関数での可解性が示されている。本小論ではそれらのmixed case、即ち作用素Pの主シンボル (P)=0}がsmooth)である場合には、Nirenberg-Treves・佐藤-柏原-河合ら(S-K-K)が、生成的な点に於いて可解性に関する必十条件を与えている。他方、より一般の多重特性的(即ち作用素Pの特性多様体が0-sectionの外で特異点又は重複点を持つ)な作用素の可解性の研究は一般に困難とされているが、佐藤超関数の枠組みではいくつかの場合にその困難が乗り越えられている。同枠組みに於いては超関数の性質を局所的に調べる場合、その特異性に着目し、解析関数をmoduloして考察する。その結果得られる「関数」をマイクロ関数といい、作用素Pの超関数としての可解性は、よく知られた解析関数での可解性(Cauchy-Kowalevskyの定理)とマイクロ関数での可解性に分解して判定する。特に作用素Pが双曲型、もしくは部分楕円型の場合はBony-Schapiraによってマイクロ関数、更には超関数での可解性が示されている。本小論ではそれらのmixed case、即ち作用素Pの主シンボル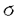 (P)が部分楕円型と双曲型の積にかけるようなPに対し、その超関数としての可解性を研究する。具体的には、 (P)が部分楕円型と双曲型の積にかけるようなPに対し、その超関数としての可解性を研究する。具体的には、 (x’=(x1,x2,…;xl))とし、その複素化を (x’=(x1,x2,…;xl))とし、その複素化を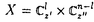 、更にはXの余接バンドルT*X∋(z; 、更にはXの余接バンドルT*X∋(z; dz)とする時、次の定理が成り立つ。 dz)とする時、次の定理が成り立つ。 Theorem1E∈DXを(Bony-Schapiraの意味で)z’-変数について部分楕円型な微分作用素、Q∈DXを±dx1-方向に双曲型でその主シンボルが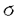 (Q)(z, (Q)(z, )=qm(z, )=qm(z, ’)の形の微分作用素とする。この時P=E・Q+(lower order terms)∈Dxとおくと、 ’)の形の微分作用素とする。この時P=E・Q+(lower order terms)∈Dxとおくと、 (i)P:BM→BMは全射的、 (ii)P:CM→CMは = = \X上全射的。 \X上全射的。 ここでBM(resp.CM)は超関数(resp.マイクロ関数)の層をあらわす。 上述の定理でQ=1とおくと、これはBony-Schapiraの部分楕円型作用素の可解性の結果をrecoverし、 と縮約すると、これは柏原-河合(’75)(あるいはBony-Schapira)が扱った作用素の可解性をrecoverする。この定理のPは、部分楕円性が障害となって双曲型にならず、更にPの特性多様体{ と縮約すると、これは柏原-河合(’75)(あるいはBony-Schapira)が扱った作用素の可解性をrecoverする。この定理のPは、部分楕円性が障害となって双曲型にならず、更にPの特性多様体{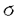 (P)=0}={ (P)=0}={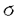 (E)=0}∪{ (E)=0}∪{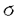 (Q)=0}は、その部分楕円因子と双曲因子が複雑に交叉する為に、上述の従来の超局所解析の方法では扱えなかった。そこで著者はこのPの可解性を研究する為にSchapira-竹内の構成したbimicrolocalizationの理論を用いた。即ちM= (Q)=0}は、その部分楕円因子と双曲因子が複雑に交叉する為に、上述の従来の超局所解析の方法では扱えなかった。そこで著者はこのPの可解性を研究する為にSchapira-竹内の構成したbimicrolocalizationの理論を用いた。即ちM= ⊂L= ⊂L=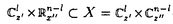 を部分複素化とする。かつて柏原-Schapiraはmicrolocalization functor を部分複素化とする。かつて柏原-Schapiraはmicrolocalization functor M: M: を定式化し、これを用いてマイクロ関数の層CMをCM= を定式化し、これを用いてマイクロ関数の層CMをCM= M(OX)[n](これは次数0に集中して層を成す)と再構成した。そのanalogyとしてSchapira-竹内はbimicrolocalization functor M(OX)[n](これは次数0に集中して層を成す)と再構成した。そのanalogyとしてSchapira-竹内はbimicrolocalization functor ML:Db(X)→ ML:Db(X)→ と片岡-戸瀬の第二マイクロ関数の層をCML= と片岡-戸瀬の第二マイクロ関数の層をCML= ML(OX)[n]とfunctorialに構成した。この層は標準的射影 ML(OX)[n]とfunctorialに構成した。この層は標準的射影 : : と正則パラメータ付きマイクロ関数の層Cx"Oz’を用いて、 と正則パラメータ付きマイクロ関数の層Cx"Oz’を用いて、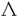 上の完全列0→ 上の完全列0→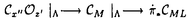 →0によって特徴付けられる。従って件の作用素Pをもう一度「超局所的に」分解すると、焦点となっているPの →0によって特徴付けられる。従って件の作用素Pをもう一度「超局所的に」分解すると、焦点となっているPの 可解性が、良く知られたCO-可解性(SchapiraのCauchy-Kowalevsky型定理)と 可解性が、良く知られたCO-可解性(SchapiraのCauchy-Kowalevsky型定理)と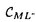 可解性に分解して判定されることが分かる。これは幾何的な観点から言えば、作用素Pの特性多様体{ 可解性に分解して判定されることが分かる。これは幾何的な観点から言えば、作用素Pの特性多様体{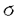 (P)=0}を (P)=0}を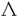 の複素化(⊂T*X)に沿って「Blow-up」し、部分楕円因子をとりはずすことによって、問題をCML-可解性に帰着することに相当する。このCML-可解性は、共著者のコホモロジー の複素化(⊂T*X)に沿って「Blow-up」し、部分楕円因子をとりはずすことによって、問題をCML-可解性に帰着することに相当する。このCML-可解性は、共著者のコホモロジー ( (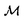 ,BM)の消滅に関するテクニックを用いて、次の導来圏での同型を示すことに帰着する。今、N={x1=0}⊂M、CNL= ,BM)の消滅に関するテクニックを用いて、次の導来圏での同型を示すことに帰着する。今、N={x1=0}⊂M、CNL= 、 、 を自然な入射のペアーとする。 を自然な入射のペアーとする。 Theorem2Pを定理1の如くとし、 とおく。このとき とおく。このとき 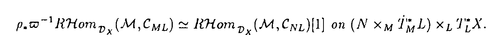 実際、上の同型と既知のdivision定理を合わせると、第二マイクロ関数に対するCauchy問題の可解性を直ちに得ることができる。この定理は層のマイクロ台の理論を用いて著者によって証明された。以上で定理1の多重特性作用素Pに対する超関数での可解性を得ることができた。更に我々は上の議論で用いたアイデアを応用し、大阿久の得た斉次境界値問題の結果を非斉次化することに成功した。 (Part2)解の延長について・その1 M= n、Nを実余次元d n、Nを実余次元d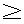 1なる部分多様体、XをMの複素化とする。M\ 1なる部分多様体、XをMの複素化とする。M\ が が ∈ ∈ の定める半空間に含まれる閉凸集合となるようにとったMの開集合 の定める半空間に含まれる閉凸集合となるようにとったMの開集合 を を -方向の定めるパックマンと呼ぶことにする。(d=1の時は -方向の定めるパックマンと呼ぶことにする。(d=1の時は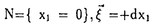 に対し、 に対し、 ={x1<0}⊂Mととる。) ={x1<0}⊂Mととる。)  図表 図表 図表 図表 このとき、N付近で定義された偏微分方程式系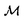 ∈coh(DX)に対し、あるパックマン ∈coh(DX)に対し、あるパックマン がとれて、 がとれて、 上の任意の実解析解(resp.超関数解)がNを突破してNの開近傍まで伸びる為の条件を考える。この種の解の延長定理はBochner型と呼ばれ、数々の研究がなされた。(解の特異点集合が超平面に含まれるくらい十分に薄い場合は金子や大阿久などによる研究もある。)解が延長する為の十分条件として適切な付加条件のもとに、楕円型(柏原-河合’72)、双曲型(柏原-Schapira)、部分楕円型、microlocally hyperbolic(竹内)の場合が知られている。本小論ではこれらの結果を「microlocally relative hyperbolic」とよばれるクラスに拡張した。簡単の為l 上の任意の実解析解(resp.超関数解)がNを突破してNの開近傍まで伸びる為の条件を考える。この種の解の延長定理はBochner型と呼ばれ、数々の研究がなされた。(解の特異点集合が超平面に含まれるくらい十分に薄い場合は金子や大阿久などによる研究もある。)解が延長する為の十分条件として適切な付加条件のもとに、楕円型(柏原-河合’72)、双曲型(柏原-Schapira)、部分楕円型、microlocally hyperbolic(竹内)の場合が知られている。本小論ではこれらの結果を「microlocally relative hyperbolic」とよばれるクラスに拡張した。簡単の為l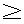 d=2、M= d=2、M= 、N={x1=x2=0}⊂Mとし、その複素化をY⊂Xとする。 、N={x1=x2=0}⊂Mとし、その複素化をY⊂Xとする。 Theorem3二つの微分作用素Pj=Ej・Qj+(lower order terms)∈DX(j=1,2)を以下の条件を満たすようにとる。 1)[E1,E2]=0かつDX/ DXEjはBony-Schapiraの意味でz’-変数について部分楕円型、 DXEjはBony-Schapiraの意味でz’-変数について部分楕円型、 2)Q1,Q2は -方向に双曲型で、各主シンボル -方向に双曲型で、各主シンボル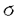 (Qj)(z, (Qj)(z, )はqj(z, )はqj(z, 1)の形にかける、 1)の形にかける、 3)[P1,P2]=0かつ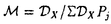 はYに沿ったマイクロ非特性条件をみたす。 はYに沿ったマイクロ非特性条件をみたす。 このとき -方向の定めるパックマン -方向の定めるパックマン が存在して、 が存在して、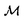 の の 上の実解析解(resp.超関数解){u;P1u=P2u=0}はNの近傍まで実解析解(rcsp.超関数解)として延びる。 上の実解析解(resp.超関数解){u;P1u=P2u=0}はNの近傍まで実解析解(rcsp.超関数解)として延びる。  図表 図表 例えばl=4( )の場合、P1=E1・Q1=(D1+ )の場合、P1=E1・Q1=(D1+ D3)・(D1+a(x")D2)、P2=E2・Q2=(D2+ D3)・(D1+a(x")D2)、P2=E2・Q2=(D2+ D4)・(D1-a(x")D2)(a(x")∈ D4)・(D1-a(x")D2)(a(x")∈ [x"])と選べる。証明のキーポイントとなるのはコホモロジーの消滅: [x"])と選べる。証明のキーポイントとなるのはコホモロジーの消滅:  で、これを層のマイクロ台の理論を用いて証明した。 (Part3)解の延長について・その2 他方、著者は共著者と共に偏微分方程式の実解析解・超関数解に対する(Bochner型などの)延長定理をC∞-解・Distribution解へと応用することを試みた。その背景には、柏原のRiemann-Hilbert対応の論文(’84)以降、tempered distributionの層がD-加群の手法を用いて定式化され、多くの研究がAndronikofらによってなされたことがある。C∞-関数についてもBonyらによってその超局所的アプローチがなされた後、Colinの学位論文(’97)によってfull-functorialに扱われるようになった。これらの理論の進展は、近年線形偏微分方程式のC∞-解やDistribution解の研究にも大きな影響を及ぼし、現在D’Agnolo-Toninらによって精力的に研究がなされている。ここでは我々の主結果を余次元 の場合(i.e. の場合(i.e. に対し、 に対し、 ={x1<0}⊂M)に限定して述べる。なおd>1の場合にも相応の延長定理を得ている。今、V=Ch ={x1<0}⊂M)に限定して述べる。なおd>1の場合にも相応の延長定理を得ている。今、V=Ch 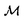 、 、 、 、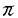 :T*X→Xとする。 :T*X→Xとする。 Theorem4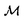 ∈coh(DX)に以下の条件を課す: ∈coh(DX)に以下の条件を課す: 1)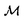 は+dx1-方向に双曲型、 は+dx1-方向に双曲型、 2) は は のsmooth regular involutive submanifoldで、Vは のsmooth regular involutive submanifoldで、Vは の近傍上 の近傍上 の複素化になっている、 の複素化になっている、 3) は は 上Vに沿って柏原-大島の意味でregular singu-larityを持つ。 上Vに沿って柏原-大島の意味でregular singu-larityを持つ。 このとき次の導来圏の等式が成り立つ:  図表 図表 この定理のsituationは当初、D’Agnolo-Toninによって考えられたが、彼等の主結果は、境界値問題を考察する限りに於いては、  となり、 の上でのdistribution解がtemperedという仮定のもとでNを超えて延長するという意味になる。我々は、この増大度条件を取り除いて、導来圏での等式を示したことになる。 の上でのdistribution解がtemperedという仮定のもとでNを超えて延長するという意味になる。我々は、この増大度条件を取り除いて、導来圏での等式を示したことになる。 最後に、数学とは直接関係のない進路を選択することになりましたが、代数解析の益々の御発展を心よりお祈りいたします。 |
| 審査要旨 | | 本論文提出者は解析関数を係数とする線形偏微分方程式系に対し,佐藤超関数やマイクロ関数における可解性と解の延長可能性に関する研究をおこなった.佐藤超関数及びマイクロ関数における線形偏微分方程式系の研究は佐藤-河合-柏原らにより始められ多くの専門家により興味深い結果が得られてきた.とくに著しいのは柏原-Schapiraらにより層のマイクロ台の理論が創始され応用されるようになってからである.この理論はもともとフランスのBony-Schapiraらが弱双曲型方程式の初期値問題の佐藤超関数の枠内での解の構成に使用した,正則関数解を実軸に接するくさび状領域まで解析接続するアイデアをコホモロジー論的に抽象化し,一般的な層複体の高次元コホモロジーの大域切断同土の同型定理に一般化したものである.このとき同型性の障害になるものがこの層複体のマイクロ台と呼ばれる集合で,基礎となる多様体の余接バンドル内の錘状閉集合として定義され,線形偏微分方程式系の場合にはいわゆる特性多様体に一致する.超関数やマイクロ関数での可解性はそれぞれ超関数およびマイクロ関数を係数とする偏微分方程式系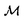 の解の層複体 の解の層複体 の1次元以上のコホモロジー群の消滅として代数的にとらえることができるが超局所化関手 Mと解層関手は交換するのでこれらはより基本的なものである正則関数解層の複体 Mと解層関手は交換するのでこれらはより基本的なものである正則関数解層の複体 から関手論的に構成される.層のマイクロ台の理論とはこのように基本的な層複体から関手論的に構成された層複体のマイクロ台を,元の層複体のマイクロ台によって幾何学的に評価する理論である.一方,可解性や解の延長可能性はこのように から構成されたある種の層複体の台やマイクロ台の消滅に帰着させることができるが から構成されたある種の層複体の台やマイクロ台の消滅に帰着させることができるが のマイクロ台は柏原によって のマイクロ台は柏原によって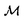 の特性多様体に一致することが示されている.従って微分方程式の超局所解析に関する問題の多くはよりよいマイクロ台の評価を得る関手の構成やマイクロ台の消滅がわかっている層複体への問題の帰着のさせ方に尽きる.この意味では本論文提出者は主に一部共著者でもある広島大学の竹内潔による,いわゆる第二超局所解析における双超局所化関手を応用してある種の方程式系に対する超関数やマイクロ関数の空間での可解性および超関数解の延長可能性に関する新しい結果を得た. の特性多様体に一致することが示されている.従って微分方程式の超局所解析に関する問題の多くはよりよいマイクロ台の評価を得る関手の構成やマイクロ台の消滅がわかっている層複体への問題の帰着のさせ方に尽きる.この意味では本論文提出者は主に一部共著者でもある広島大学の竹内潔による,いわゆる第二超局所解析における双超局所化関手を応用してある種の方程式系に対する超関数やマイクロ関数の空間での可解性および超関数解の延長可能性に関する新しい結果を得た. 本論文は大きく3部からなり,そのうち第1部と3部は広島大学の竹内潔氏との共同研究である.第1部では偏微分作用素Pのマイクロ関数での可解性を扱い,その可解性を双マイクロ関数における可解性に帰着させた上で双超局所化関手の理論を通常のいわゆる正則部分多様体に沿っての第二超局所解析に応用し可解となるべき次のような主シンボルPに対する一つの十分条件を与えた:ある空間変数xの直積分割x=(x’,x")が存在して と因数分解できてE(x, )はx’-変数について部分楕円型,Q(x, )はx’-変数について部分楕円型,Q(x, ’)は変数x"に関する偏微分を含まない弱双曲型作用素になるときである.第2部では高余次元境界付近での偏微分方程式系に対する超関数解および実解析解のBochner型延長可能性を扱い,次のような十分条件を得た:高余次元境界が ’)は変数x"に関する偏微分を含まない弱双曲型作用素になるときである.第2部では高余次元境界付近での偏微分方程式系に対する超関数解および実解析解のBochner型延長可能性を扱い,次のような十分条件を得た:高余次元境界が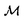 に対してマイクロ非特性的,かつ に対してマイクロ非特性的,かつ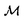 の包合的ベースとなる偏微分作用素の組P1,…,Pl(lは境界の余次元)で第1部の作用素のようなシンボルに関する分解表示をもつものが存在するときである.証明は第1部の議論をさらに高余次元境界値理論と組み合わせて得られ,やはり双超局所化関手の性質が決定的役割を果たす.第3部はやや異なり,量子化接触変換の下でのマイクロ台や定義関数の緩増加増大性の不変性を使い,特性多様体に沿って確定特異性をもつ双曲型方程式系のディストリビューション解の延長可能性定理を得ている. の包合的ベースとなる偏微分作用素の組P1,…,Pl(lは境界の余次元)で第1部の作用素のようなシンボルに関する分解表示をもつものが存在するときである.証明は第1部の議論をさらに高余次元境界値理論と組み合わせて得られ,やはり双超局所化関手の性質が決定的役割を果たす.第3部はやや異なり,量子化接触変換の下でのマイクロ台や定義関数の緩増加増大性の不変性を使い,特性多様体に沿って確定特異性をもつ双曲型方程式系のディストリビューション解の延長可能性定理を得ている. 全体として上記の竹内潔氏の双超局所化関手の理論または緩増加増大性の量子化接触変換などのアイデアが指導的役割を果たしてはいるが一部共同研究とはいえ,最新かつ難解な双超局所化関手の理論を具体的な偏微分方程式の問題に適用して新しい結果を導出したことは高く評価できる.また第2部では金子や大阿久などこの方面の先駆者達の結果に並びうる,延長可能性に関する新しくかつ興味深い結果を独力で得たことは十分な問題解決能力を備えていることを証明している.よって,論文提出者小清水寛は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. |