| 内容要旨 | | 三次元多様体のTuraev-Viro-Ocneanu不変量[O]は、三次元多様体の三角形分割にもとずいて定義されるTuraev-Viro不変量[TV]の一般化である。Turaev-Viro-Ocneanu不変量においては、Turaev-Viro不変量の場合とは異なり、intertwinerの空間の次元は2以上となりうるため、三角形分割の辺だけでなく面へのcoloringを考える必要がある。Turaev-Viro-Ocneanu不変量は、hyperfinite II1-subfactorのAn,D2n,E6,E8 Coxeter graphによる分類理論であらわれるparagroupから得られるquantum 6j-symbolを用いて構成される[EK]。Ak+1Coxeter graphに対応する不変量はSU(2)level kのTuraev-Viro不変量であるが、E6,E8 Coxeter graphに対応する不変量に関しては、具体的な不変量の計算はまだあまりなされていない。 この論文では、E6 Coxeter graphをprincipal graphに持つE6 subfactorから得られるE6 quantum 6j-symbolによるE6 Turaev-Viro-Ocneanu不変量について調べた。 三次元多様体のTuraev-Viro-Ocneanu不変量は、以下のように定義される[EK]。閉じた三次元多様体Mの三角形分割Tと、その頂点の順序を固定し、辺には頂点の順序から決まる向きを入れておく。各向き付けられた辺| 01|(0<1)に、fusion rule algebra Aの基底{Xi}の元を対応させる。(辺のcoloringという。)  各面|012|(0<1<2)には、その三辺のcoloringにより対応するintertwinerの空間の正規直交基底{si}の元を対応させる。(面のcoloringという。)  各単体 には、これらの辺と面のcoloringにより色付けが定まり、これらの色付けられた単体(, , )に対してquantum 6j-symbolと呼ばれる複素数Z(,,)が定まる。さらに、fusion rule algebra Aから正の実数へのhomomorphismであるquantum dimension 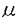 (Xi)が定まっている。三次元多様体のTuraev-Viro-Ocneanu不変量は以下のように定義される。 Definition閉じた三次元多様体Mの三角形分割Tに対して、Turaev-Viro-Ocneanu不変量は以下のように定義される。  ここで、＝#{vertices of T}, ＝ i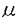(Xi)2である。 この値は、quantum 6j-symbolのtetrahedral symmetryにより頂点の順序によらず、quantum 6j-symbolのunitarityとpentagon identityにより三角形分割のPachner move[P]のもとで不変になり、三次元多様体Mの不変量となる。 次に、E6 subfactor N⊂Mとは、hyperfinite II1-subfactorで、そのbimoduleとしてのrelative tensor productによる乗法規則を表すprincipal graphがE6 Coxetergraphとなるものである。特に、E6 principal graphの3つのeven vertexに対応するbimoduleid,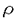 , により生成されるfusion rule algebraを考える。これは次のような乗法規則を持っている。  図表 これから、intertwinerの空間 の次元は2であることがわかる。量子群の表現環の場合と同様にして、このfusion rule algebraからE6 quantum 6j-symbolが得られる。このE6 quantum 6j-symbolは、M.Izumiによりsector theoryを用いてもとめられている[Iz1]。 このE6 quantum 6j-symbolを用いて、レンズ空間L(p,1)に対してE6 Turaev-Viro-Ocneanu不変量の値は以下のように計算される。 Propositionレンズ空間L(p,1)のE6 Turaev-Viro-Ocneanu不変量の値は以下で与えられる。  これにより、レンズ空間L(p,1)の不変量Z(L(p,1))は周期12を持つことがわかり、以下のような表を得る。  図表 この表から、不変量Z(L(p,1))はp＝12k+3,12k+4,12k+8,12k+9のときTuraev-Viro不変量の場合とは異なり複素数値をとり、向きの異なるL(p,1)とL(p,p-1)を区別できることがわかる。 次に、曲面とその三角形分割Kに対して、Hilbert空間V(,K)を以下のように定義する。(K上のcoloringたちが正規直交基底になっている。)  さらに、三次元多様体Mに境界があるときにも、境界上で三角形分割とそのcoloringを固定することにより同様に不変量を定義することができ、それを用いてcobordism(W,0,1)に対して線形写像 ((W,0,1))が定義される。  Hilbert空間V(,K)をtrivial cobordism(×[0,1],,)による線形写像((×[0,1],,))の核で割ることにより、三角形分割KによらないHilbert空間H()を得る。  線形写像((W,0,1))は線形写像((W,0,1))を誘導する。  そして、つぎが成立する。  これにより、曲面とcobordismの圏から線形空間と線形写像の圏への関手(H(・),(・))が得られる。この関手は、Turaev-Viro-Ocneanu不変量から導かれるTQFTと呼ばれる。 E6 Turaev-Viro-Ocneanu不変量の場合に、曲面としてtorusT2をとりcobordismとしてmapping cylinderをとることにより、torusT2のmapping class groupの10次元Hilbert空間H(T2)への表現を得る。 Theorem E6 Turaev-Viro-Ocneanu不変量から導かれるTQFTにより、SL2(Z)の10次元Hilbert空間H(T2)への表現を(具体的に)得る。(Theorem.4.7参照。)また、いくつかの(p,q)に対して、レンズ空間L(p,q)の不変量Z(L(p,q))をもとめることができる。 さらに、genus gが2以上の曲面gに対してもmapping class group 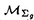 の表現H(g)を考えることができるが、これらの表現の次元は以下のようにもとめることができる。 Theorem Hilbert空間H(g)の次元は以下で与えられる。  これにより、以下のような表を得る。  図表 A cknowledgments和久井道久先生には、不変量の計算方法について教えて頂きました。深く感謝いたします。また、泉正己先生、河東泰之先生には、subfactor理論についていろいろ教えて頂きました。深く感謝いたします。最後になりましたが、河野俊丈先生には有用な助言をして頂きました。深く感謝いたします。 References[A]M.F.Atiyah,Topological quantum field theories,Publ.Math.I.H.E.S.68(1989)175-186.[B]J.Birman,Braids,Links and Mapping Class Groups,Princeton Univ.Press.[EK]D.E.Evans,Y.Kawahigashi,Quantum symmetries on operator algebras,Oxford University Press(1998).[Iz1]M.Izumi,Subalgebras of Infinite C*-Algebras with Finite Watatani Indices I:Cuntz Algebras,Commun.Math.Phys.155(1993)157-182.[Iz2]M.Izumi,Subalgebras of Infinite C*-Algebras with Finite Watatani Indices II:Cuntz-Krieger Algebras,Duke Math.Journal Vol.91,No.3(1998)409-461.[Iz3]M.Izumi,The Structure of Sectors Associated with Longo-Rehren Inclusions,preprint.[Iz4]M.Izumi,private communications,.[O]A.Ocneanu,Quantized group, string algebras and Galois theory for algebras,Operator algebras and applications Vol.2(Warwick 1987)(ed.D.E.Evans and M.Takesaki)London Math.Soc.Lecture Note Series Vol.136,119-172(1988).[OS]M.Okamoto,C.Sato,,RIMS Kokyuroku 1053(1998).[P]U.Pachner,P.L.homeomorphic manifolds are equivalent by elementary shellings,Europ.J.Comb.12(1991)129-145.[R]D.Rolfsen,Knots and Links,Publish or Perish Inc..[TV]V.G.Turaev,O.Ya.Viro,State sum invariants of 3-manifolds and quantum 6j-symbols,Topology 31(1992)865-902.[W1]M.Wakui,On Dijkgraaf-Witten invariant for 3-manifolds,Osaka J.Math.29(1992)675-696.[W2]M.Wakui,Fusion Algebras for Orbifold Models(A Survey),Topology,Geometry and Field Theory 225-235,World Scientific Publ.(1994).[W3]M.Wakui,private communications,. |